Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Математические модели в экономике.doc
Добавлен: 25.10.2023
Просмотров: 140
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, полученный при использовании канонической формы с переменными x5, x6, x7.
Шаг 1. Формирование показателей корректирующей строки и расчет F.
Шаг 2. Переходим к табл. 3.7 – заполнение столбца N1.
Шаг 3. Расчет показателей первой индексной строки.
Шаг 4. Проверка условия оптимальности.
Шаг 5. Выбор ключевого столбца – переходим к табл. 3.8 (x2).
Шаг 6. Формирование показателей исходной строки.
Шаг 7. Формирование показателей ключевого столбца в табл. 3.8.
Шаг 8. Выбор ключевой строки: min {12/4; 8/2; 48/8} = 12/4. Переменная x2 вводится в базис, переменная x5 исключается из базиса. Переходим к табл. 3.9.
Таблица 3.8
Шаг 9. Симплексные преобразования.
Шаг 1. Формирование показателей корректирующей строки табл. 3.9 и расчет F.
Шаг 2. Переходим к табл. 3.7 – заполнение столбца N2.
Шаг 3. Расчет показателей второй индексной строки.
Шаг 4. Проверка условия оптимальности.
Шаг 5. Выбор ключевого столбца – переходим к табл. 3.9 (x3).
Шаг 6. Формирование показателей исходной строки табл. 3.9.
Шаг 7. Формирование показателей ключевого столбца в табл. 3.9.
Шаг 8. Выбор ключевой строки. Переменная x3 вводится в базис, переменная x6 исключается из базиса.
Переходим к табл. 3.10.
Таблица 3.9
Шаг 9. Симплексные преобразования.
Шаг 1. Формирование показателей корректирующей строки табл. 3.10 и расчет F.
Шаг 2. Переходим к табл. 3.7 – заполнение столбца N3.
Шаг 3. Расчет показателей третьей индексной строки.
Шаг 4. Проверка условия оптимальности. План оптимален.
Таблица 3.10
3.3 Решение задачи симплекс-методом с использованием
искусственного базиса
1. Необходимо составить оптимальную диету, закупив три вида продуктов B1, B2, B3 c заданными ценами С1, С2, С3. Составленная диета должна удовлетворять по объему требуемых питательных веществ на уровне не ниже заданного и быть минимальной по затратам.
2. Сформировать математическое описание задачи.
3. Построить каноническую форму, искусственный базис и получить допустимое решение.
4. Определить оптимальный план.
5. Выполнить анализ оптимального плана, включая состав и объем закупленных продуктов, расходы, количество и эффективность питательных веществ.
6. Проанализировать возможность изменения оптимального плана, привлекая для этого двойственные оценки и другие показатели индексной строки.
Исходные данные приведены в табл. 3.11–3.13.
Каждый студент получает свой вариант расчета – двухзначный шифр. Выбор варианта определяется порядковым номером фамилии студента в журнале группы.
В табл. 3.11 приведены данные по количеству питательных веществ в каждом продукте – общие для всех вариантов. В табл. 3.12 приведены данные по коэффициентам целевой функции по вариантам с первой цифрой шифра. В табл. 3.13 приведены данные по ресурсам по вариантам со второй цифрой шифра.
Алгоритм симплекс-метода в задаче с искусственным базисом также состоит из двух этапов. На первом осуществляется построение канонической формы – допустимого плана с использованием искусственного базиса. При этом дополнительные неизвестные имеют знак «–», а их коэффициенты в целевой функции равны нулю, искусственные переменные имеют знак «+», а их коэффициенты в целевой функции равны достаточно большому числу М. На втором этапе выполняется обычная оптимизационная процедура.
Шаг 1. Построение канонической формы. Для каждого ограничения вводим
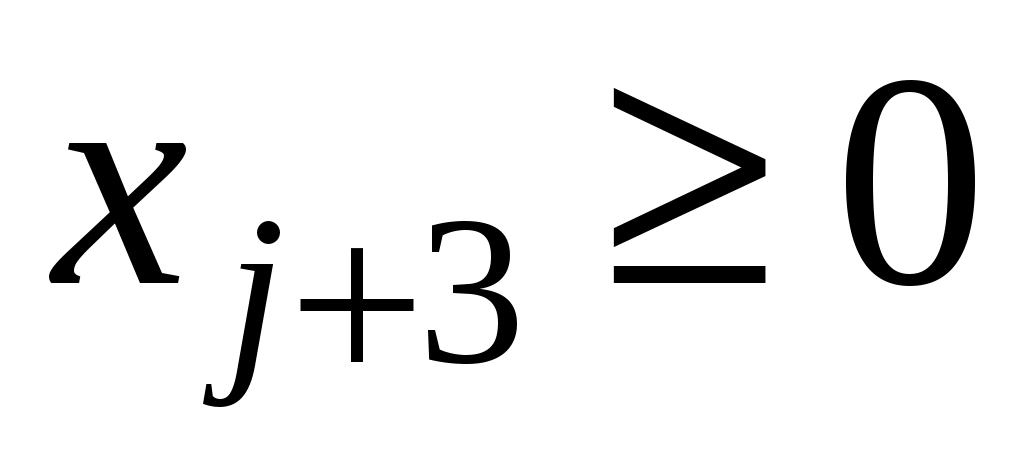– дополнительную переменную;
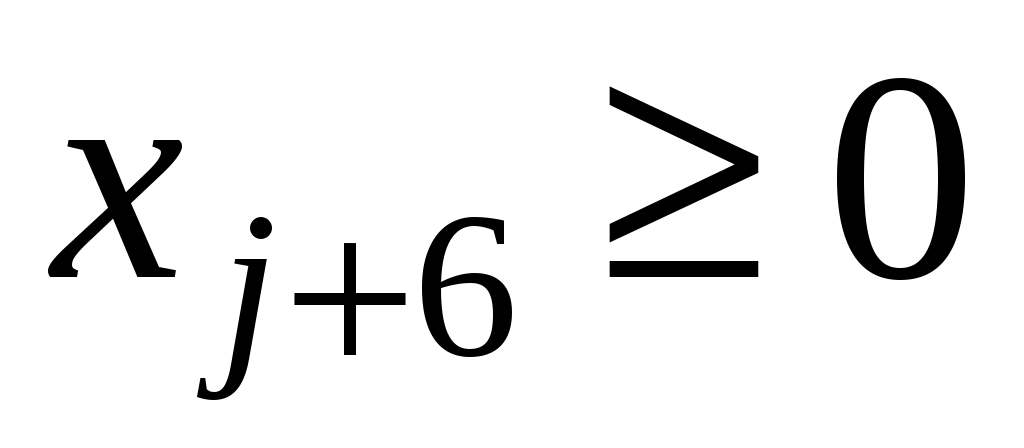– переменную искусственного базиса.
Шаг 2. Строится базис допустимого плана относительно переменных искусственного базиса.
Шаг 3. Рассчитываются симплекс-множители и показатели
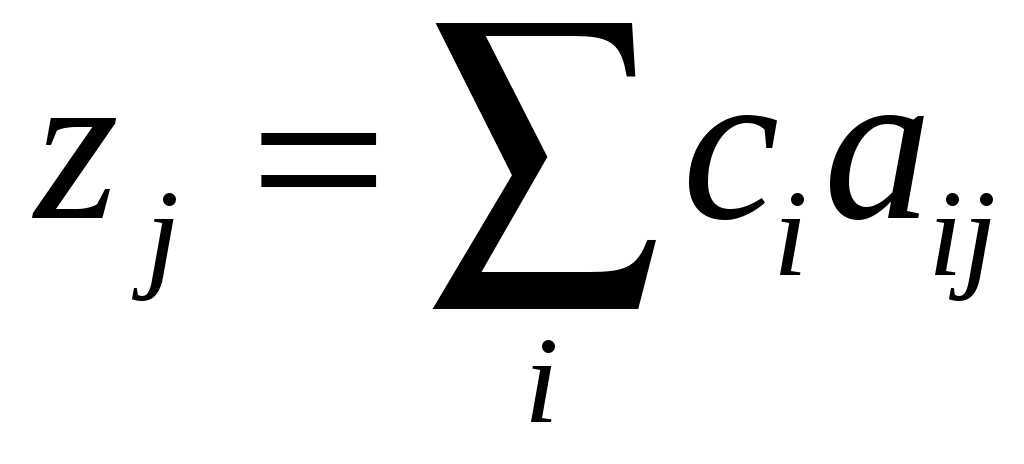
строки относительных показателей (индексной строки):
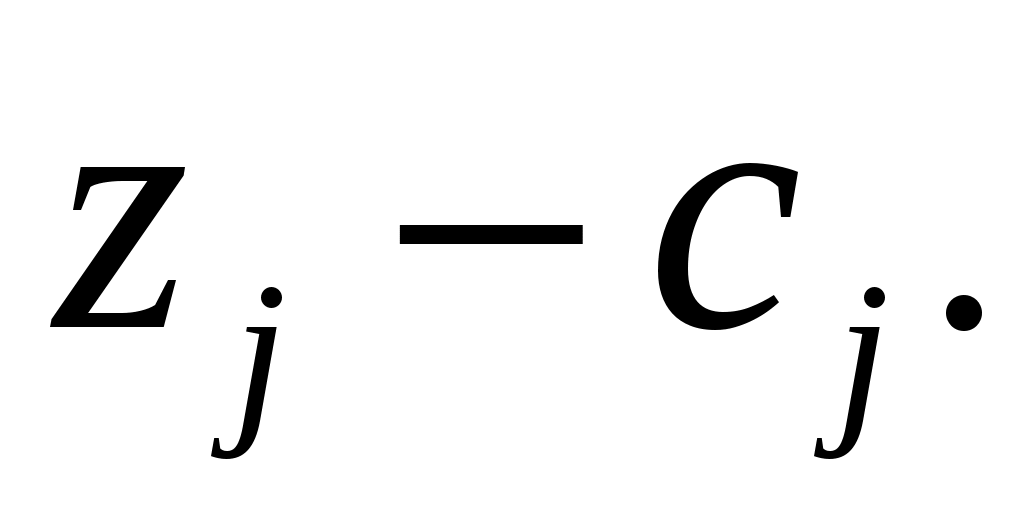
Шаг 4. Выполняется проверка решения на оптимальность. Для задач на минимум целевой функции должно выполняться условие:
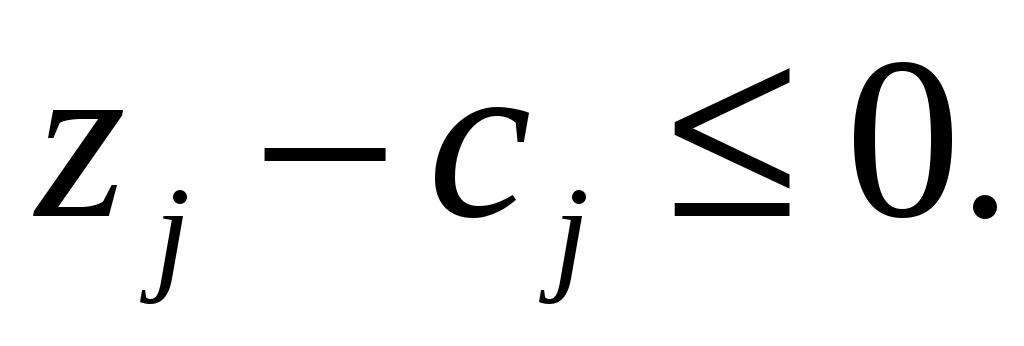
Если условие оптимальности не выполняется, переходим к шагу 5, иначе получен оптимальный и допустимый план.
Шаг 5. Выбор ключевого столбца. Из показателей индексной строки выбирается значение с наибольшим отклонением от условия оптимальности. Соответствующая переменная на следующей итерации входит в базис задачи.
Шаг 6. Выбор ключевой строки. Находится минимальное отношение показателей столбцов xi и aij при условии, что aij > 0.
Шаг 7. Выполняются симплекс-преобразования.
Пример 3.3. Вначале заполняется таблица 3.14. Сюда занесем значения коэффициентов функции цели, наименования неизвестных, массив значений коэффициентов «затраты – выпуск», элементы столбцов ci, pi, xi – cоставляющих базис плана, полученный при использовании канонической формы с переменными x7, x8, x9.
Таблица3.14
Шаг 1. Формирование показателей корректирующей строки и расчет F.
Шаг 2. Переходим к табл. 3.7 – заполнение столбца N1.
Шаг 3. Расчет показателей первой индексной строки.
Шаг 4. Проверка условия оптимальности.
Шаг 5. Выбор ключевого столбца – переходим к табл. 3.8 (x2).
Шаг 6. Формирование показателей исходной строки.
Шаг 7. Формирование показателей ключевого столбца в табл. 3.8.
Шаг 8. Выбор ключевой строки: min {12/4; 8/2; 48/8} = 12/4. Переменная x2 вводится в базис, переменная x5 исключается из базиса. Переходим к табл. 3.9.
Таблица 3.8
| ci | pi | xi | 4 | 2 | 8 | |
| 0 | x5 | 12 | 1 | 0 | 0 | 4 |
| 0 | x6 | 8 | 0 | 1 | 0 | 2 |
| 0 | x7 | 48 | 0 | 0 | 1 | 8 |
| | | 0 | 0 | 0 | 0 | |
Шаг 9. Симплексные преобразования.
Шаг 1. Формирование показателей корректирующей строки табл. 3.9 и расчет F.
Шаг 2. Переходим к табл. 3.7 – заполнение столбца N2.
Шаг 3. Расчет показателей второй индексной строки.
Шаг 4. Проверка условия оптимальности.
Шаг 5. Выбор ключевого столбца – переходим к табл. 3.9 (x3).
Шаг 6. Формирование показателей исходной строки табл. 3.9.
Шаг 7. Формирование показателей ключевого столбца в табл. 3.9.
Шаг 8. Выбор ключевой строки. Переменная x3 вводится в базис, переменная x6 исключается из базиса.
Переходим к табл. 3.10.
Таблица 3.9
| ci | pi | xi | 0 | 2 | 4 | |
| 4 | x2 | 3 | 1/4 | 0 | 0 | 0 |
| 0 | x6 | 2 | –1/2 | 1 | 0 | 2 |
| 0 | x7 | 24 | –2 | 0 | 1 | 4 |
| | | 12 | 1 | 0 | 0 | |
Шаг 9. Симплексные преобразования.
Шаг 1. Формирование показателей корректирующей строки табл. 3.10 и расчет F.
Шаг 2. Переходим к табл. 3.7 – заполнение столбца N3.
Шаг 3. Расчет показателей третьей индексной строки.
Шаг 4. Проверка условия оптимальности. План оптимален.
Таблица 3.10
| ci | pi | xi | | | |
| 4 | x2 | 3 | 1/4 | 0 | 0 |
| 3 | x3 | 1 | –1/4 | 1/2 | 0 |
| 0 | x7 | 20 | –1 | –2 | 1 |
| | | 15 | 1/4 | 3/2 | 0 |
3.3 Решение задачи симплекс-методом с использованием
искусственного базиса
1. Необходимо составить оптимальную диету, закупив три вида продуктов B1, B2, B3 c заданными ценами С1, С2, С3. Составленная диета должна удовлетворять по объему требуемых питательных веществ на уровне не ниже заданного и быть минимальной по затратам.
2. Сформировать математическое описание задачи.
3. Построить каноническую форму, искусственный базис и получить допустимое решение.
4. Определить оптимальный план.
5. Выполнить анализ оптимального плана, включая состав и объем закупленных продуктов, расходы, количество и эффективность питательных веществ.
6. Проанализировать возможность изменения оптимального плана, привлекая для этого двойственные оценки и другие показатели индексной строки.
Исходные данные приведены в табл. 3.11–3.13.
Каждый студент получает свой вариант расчета – двухзначный шифр. Выбор варианта определяется порядковым номером фамилии студента в журнале группы.
В табл. 3.11 приведены данные по количеству питательных веществ в каждом продукте – общие для всех вариантов. В табл. 3.12 приведены данные по коэффициентам целевой функции по вариантам с первой цифрой шифра. В табл. 3.13 приведены данные по ресурсам по вариантам со второй цифрой шифра.
| Таблица 3.11
| Таблица 3.12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица 3.13
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Алгоритм симплекс-метода в задаче с искусственным базисом также состоит из двух этапов. На первом осуществляется построение канонической формы – допустимого плана с использованием искусственного базиса. При этом дополнительные неизвестные имеют знак «–», а их коэффициенты в целевой функции равны нулю, искусственные переменные имеют знак «+», а их коэффициенты в целевой функции равны достаточно большому числу М. На втором этапе выполняется обычная оптимизационная процедура.
Шаг 1. Построение канонической формы. Для каждого ограничения вводим
– дополнительную переменную; – переменную искусственного базиса.Шаг 2. Строится базис допустимого плана относительно переменных искусственного базиса.
Шаг 3. Рассчитываются симплекс-множители и показатели
строки относительных показателей (индексной строки):
Шаг 4. Выполняется проверка решения на оптимальность. Для задач на минимум целевой функции должно выполняться условие:
Если условие оптимальности не выполняется, переходим к шагу 5, иначе получен оптимальный и допустимый план.
Шаг 5. Выбор ключевого столбца. Из показателей индексной строки выбирается значение с наибольшим отклонением от условия оптимальности. Соответствующая переменная на следующей итерации входит в базис задачи.
Шаг 6. Выбор ключевой строки. Находится минимальное отношение показателей столбцов xi и aij при условии, что aij > 0.
Шаг 7. Выполняются симплекс-преобразования.
Пример 3.3. Вначале заполняется таблица 3.14. Сюда занесем значения коэффициентов функции цели, наименования неизвестных, массив значений коэффициентов «затраты – выпуск», элементы столбцов ci, pi, xi – cоставляющих базис плана, полученный при использовании канонической формы с переменными x7, x8, x9.
Таблица3.14
| | | | 5 | 4 | 2 | 0 | 0 | 0 | M | M | M |
| ci | pi | xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| M | x7 | 20 | 0 | 2 | 1 | –1 | 0 | 0 | 1 | 0 | 0 |
| M | x8 | 8 | 2 | 4 | 0 | 0 | –1 | 0 | 0 | 1 | 0 |
| M | x9 | 60 | 10 | 4 | 2 | 0 | 0 | –1 | 0 | 0 | 1 |
| | | 88M | 12M | 10M | 3M | –M | –M | –M | 0 | 0 | 0 |
| | | –5 | –4 | –2 | 0 | 0 | 0 | 0 | 0 | 0 |