Таблица 1.8

	j = 1		j = 2		j = 3		j = 4		j = 5
	Пр	С/с	Пр	С/с	Пр	С/с	Пр	С/с	Пр	С/с
i = 1	2	10	2	20	2	15	2	20	1	40
i = 2	2	25	1	25	1	30	2	20	2	20
i = 3	2	20	1	20	2	25	1	20	2	35

Математическая модель обобщенной (распределительной) транспортной задачи состоит в следующем.

Найти

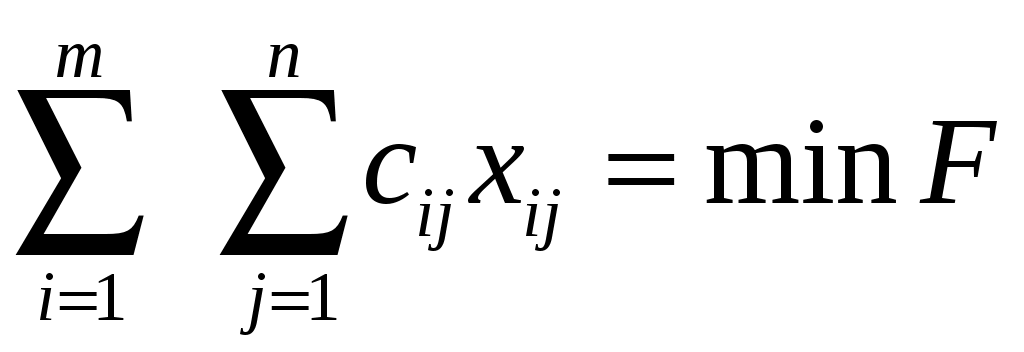(1.7)

при условии:

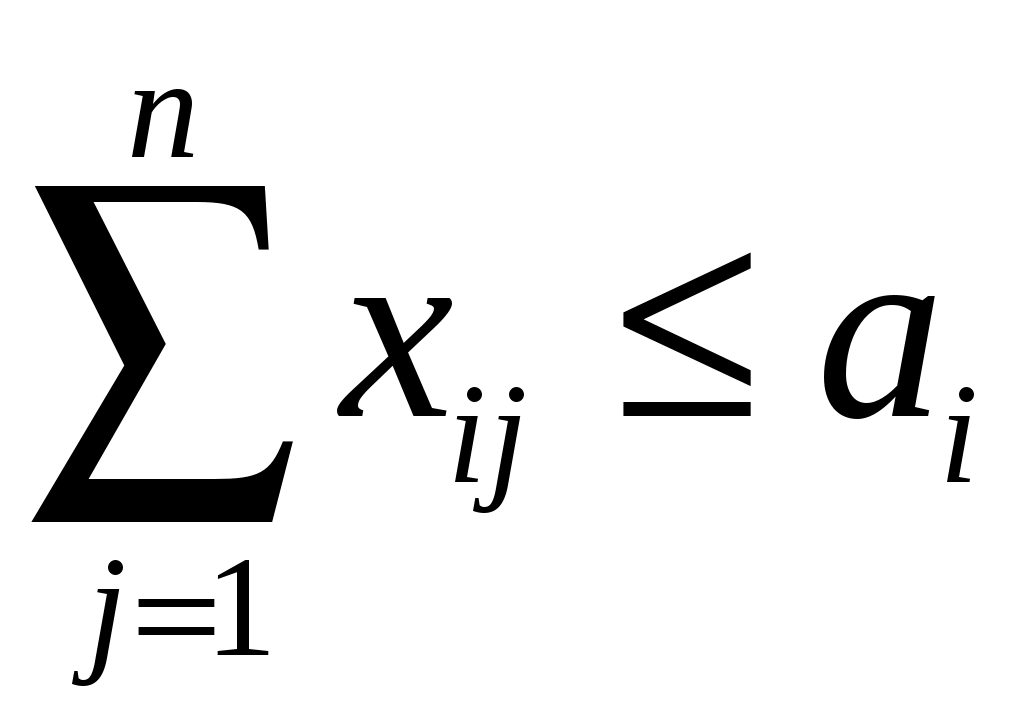, i= 1, 2, …, m; (1.8)

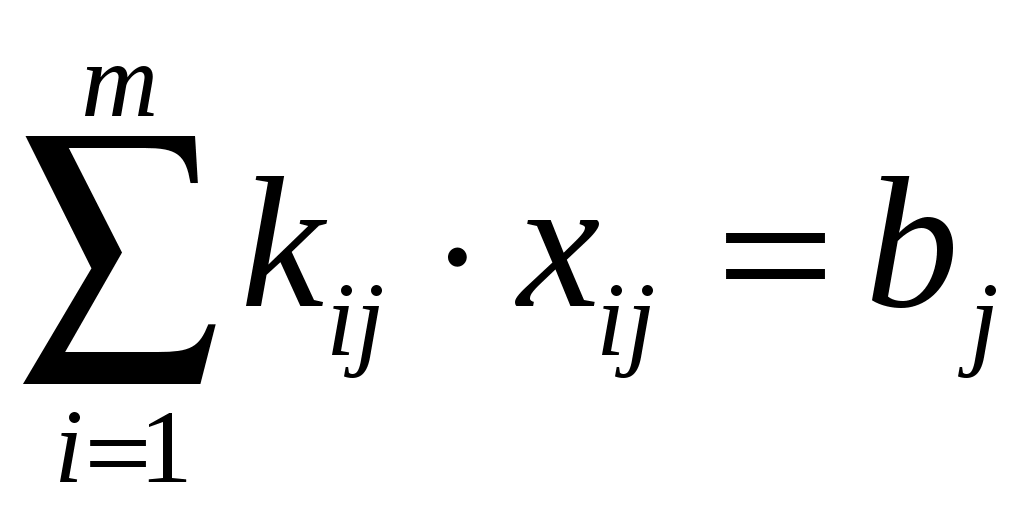, j = 1, 2, …, n; (1.9)

, (1.10)
где i – индекс ресурсов;

j – индекс производимой продукции, работы, выполняемых перевозок;

k_ij – производительность ресурсов i при выполнении работы j;

x

---

_ij – неизвестное, характеризующее объем ресурсов i, используемых при выполнении работы j;

c_ij – расходы, связанные с использованием единицы ресурсов i при выполнении работы j;

a_i – ресурсы с номером i_;

b_j – потребность (работа) с номером j.

Алгоритм модифицированного метода потенциалов состоит из двух этапов. На первом этапе осуществляется построение допустимого плана.

---

Шаг 1. Построение базиса выполняется с учетом минимальной стоимости ресурса и максимальной производительности его использования. Для этого в каждом столбце отыскивается клетка с максимальным показателем производительности (k_ij) и минимумом стоимости (с_ij).

Можно, например, воспользоваться известными методами построения допустимого плана транспортной задачи Мюллера – Мербаха или другими, рассмотренными на первом занятии. Найденный оптимальный план не обязательно должен содержать в точности n + m –1 элементов базиса. Если одна строка или более содержат резервы ресурсов, соответствующие строки получают потенциалы, равные нулю. Поэтому количество базисных элементов может быть и меньше, чем в обычной транспортной задаче подобной размерности, но их достаточно для расстановки потенциалов. Если план оказывается вырожденным, он дополняется фиктивными базисными клетками с нулевыми значениями по собственному выбору. Сама базисная клетка, помимо показателей k_ij и с_ij,содержит еще два показателя: работы и затраченных ресурсов, необходимых для выполнения этой работы.

На втором этапе выполняются итеративные процедуры оптимизации базиса задачи.

Шаг 2. Выполняется расстановка потенциалов по базисным элементам матрицы по формулам:
(1.11)

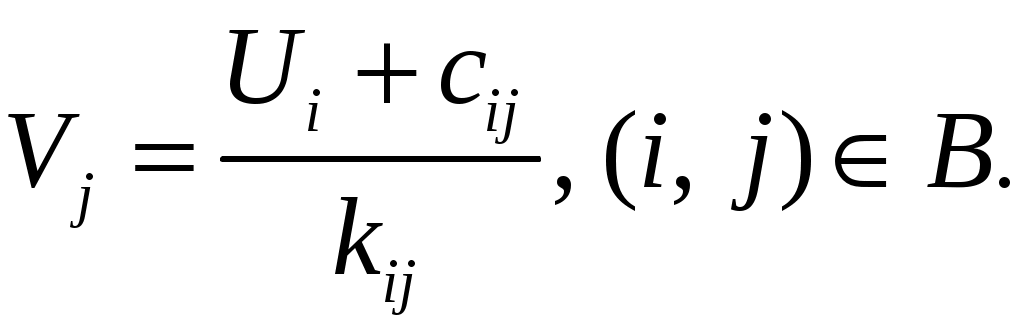(1.12)
Расстановка потенциалов начинается с одной из строк, имеющих резерв неиспользованных ресурсов. Такой строке присваивается потенциал, равный нулю.

Шаг 3. Решение проверяется на оптимальность. Должны выполняться условия:
(1.13)

(1.14)
Если условия не выполняются, переходят к шагу 4, иначе получаем оптимальный и допустимый план.

Шаг 4. Построение нового базиса. Отыскивается небазисная клетка с наибольшим нарушением условия оптимальности, относительно которой строится контур перераспределения элементов базиса.

---

Существуют два типа контуров. Первый – замкнутого вида, почти аналогичен контуру, построенному по методу потенциалов при решении обычных транспортных задач. Отличием этого контура служит цепочка (шлейф), которая соединяет элементы контура с базисной клеткой, размещенной в n + 1 столбце с резервами ресурсов. Другой контур – открытого типа, по аналогии с методом разрешающих слагаемых включает в себя два элемента n + 1 столбца с резервами ресурсов. После построения нового базиса с учетом расчетов по найденному контуру переходим к шагу 2.

Рассмотрим решение примера, приведенное в табл. 1.9–1.11. Пусть задана производственная программа по выпуску пяти видов изделий с помощью трех видов ресурсов. Исходные данные по программе, ресурсам, производительности и затратам на единицу ресурсов приведены в табл. 1.9.
Таблица 1.9

Ресурсы	350	150	150	100	150	Небаланс	Ui
300	2 10	2 15	2 20	2 20	1 40
100	2 25	1 30	1 25	2 20	2 20
200	2 20	1 25	2 20	1 20	2 35
Vj

В табл. 1.10 приведен первый базисный план.
Таблица 1.10

Ресурсы	350	150	150	100	150	Небаланс	Ui
300	2 10 350 175	2 15 150 75	2 20 100 50	2 20 *	1 40		0
100	2 25	1 30	1 25	2 20 100 50	2 20 100 50		15
200	2 20	1 25	2 20 50 25	1 20	2 35 50 25	150	0
Vj	5	7,5	10	17,5	17,5

---

Шаг 1. В первом столбце отыскивается клетка с наилучшими показателями – наименьшей стоимостью – клетка (1,1), в которую вписывается максимальный объем работы, соответствующий потребности 350 ед. С учетом производительности (k₁₁ = 2) расход соответствующих ресурсов составит: 350 : 2 = 175 ед. Остатки ресурсов составят: 300 – 175 = 125. Переходим ко второму столбцу. Здесь наиболее благоприятная клетка (1,2). Сюда назначается также максимальный объем работы, соответствующий потребности 150 ед., для чего необходимо еще 75 ед. ресурсов первого вида. Остаток последних теперь: 125 – 75 = 50. И так далее производится формирование базиса вплоть до клетки (3,5).

Шаг 2. Расстановка потенциалов начинается с третьей строки, имеющей резерв неиспользованных ресурсов. Такой строке присваивается потенциал U₃ = 0.

Шаг 3. Выполняется проверка решения на оптимальность. Поскольку у клетки (1,4) условия не выполняются, переходим к шагу 4.

Шаг 4. Построение контура для клетки (1,4). Первая цепь контура: (1,4) – (1,3) – (3,3) – (3,6). Вторая цепь контура: (1,4) – (2,4) – (2,5) – (3,5) – (3,6). Помечаем элементы первой цепочки: (1,4)⁺– (1,3)^–– (3,3)⁺– (3,6)^–, второй цепочки: (1,4)⁺– (2,4)^–– (2,5)⁺– (3,5)^–– (3,6)⁺. Из показателей объемов работ клеток, помеченных знаком «–», отыскивается наименьшее значение – 50 – клетка (3,5). Эта величина заносится в клетку (1,4), и, начиная отсюда, выполняется распределение работ и ресурсов по остальным элементам контура с учетом знаков элементов и значений показателей k_ij соответствующих клеток: (1,4) – 50/25, (1,3) – 50/25, (3,3) – 100/50, (2,4) – 50/25, (2,5) – 150/75. Клетка (3,5) из базиса выбывает. Переходим к шагу 2. Новый план приведен в табл. 1.11.
Таблица 1.11

Ресурсы	350	150	150	100	150	Небаланс	Ui
300	2 10 350 175	2 15 150 75	2 20 50 25	2 20 50 25	1 40		0
100	2 25	1 30	1 25	2 20 50 25	2 20 150 75		0
200	2 20	1 25	2 20 100 50	1 20	2 35	150	0
Vj	5	7,5	10	10	10

---

Смотрите также файлы

• Транспортная логистика (часть 11) Кокурин Д. И.pdf

• Практическая работа Задание.docx

• Кафедра доклад по дисциплине Тема Синектика Студент(ка) Козлова Ангелина Юрьевна Л112211 группы.docx

• Функция Назначение.docx

• Баллов 1 из Отметить вопрос.pdf