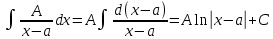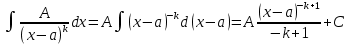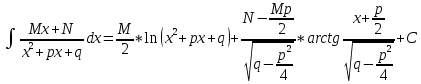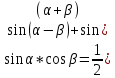Файл: Задача Скорость прямолинейного движения SS(tt)S(t).docx
Добавлен: 25.10.2023
Просмотров: 104
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Всякую правильную дробь  , знаменатель которой разложен на множители Q(x)= (x-x1)k1(x-x2)k2…(x2+p1x+q1)S1…( x2+pmx+qm)Sm можно представить и при том единственным образом в виде следующей суммы простейших дробей
, знаменатель которой разложен на множители Q(x)= (x-x1)k1(x-x2)k2…(x2+p1x+q1)S1…( x2+pmx+qm)Sm можно представить и при том единственным образом в виде следующей суммы простейших дробей 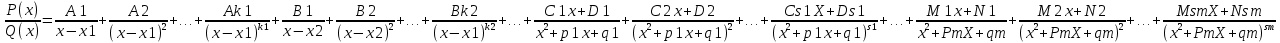
26. Интегрирование простейших рациональных дробей. Интегрирование рациональных дробей.
Простейших дробей:
Интегрирование рациональных дробей:
27. Интегрирование тригонометрических ф-й. Интегрирование иррациональных ф-й.
Универсальная тригонометрическая подстановка
R – знак рациональной функции.
Вычисление неопределённых интегралов типа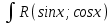 dx сводится к вычислению интегралов от рациональной функции подстановкой
dx сводится к вычислению интегралов от рациональной функции подстановкой 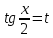 , которая называется универсальной.
, которая называется универсальной.
Другие подстановки:
Интегралы типа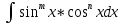
Использование тригонометрических преобразований
Интегралы типа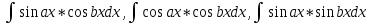
с помощью:
Интегрирование иррациональных функций
Интегралы типа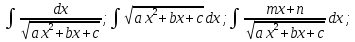 - неопределённые интегралы от иррациональных ф-й
- неопределённые интегралы от иррациональных ф-й
Тригонометрическая подстановка:
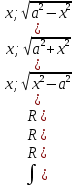 ,
,
x=asint – для интегралов 1 типа, x=atgt – 2 типа, x=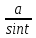 - 3 типа
- 3 типа
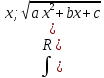 . Интегралы указанного вида приводятся к интегралам, которые можно вычислить с помощью соответствующих подстановок.
. Интегралы указанного вида приводятся к интегралам, которые можно вычислить с помощью соответствующих подстановок.
 28. Определённый интеграл как предел интегральной суммы. Геометрический и физический смысл определённого интеграла.
28. Определённый интеграл как предел интегральной суммы. Геометрический и физический смысл определённого интеграла.
Пусть ф-я y=f(x) определена на отрезке [a;b], a
Теорема Коши (существования опр. Интеграла): если ф-я y=f(x) непрерывна на отрезке [a;b], то определённый интеграл существует. (достаточное условие)
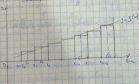 Геометрический смысл определённого интеграла: определённый интеграл от неотрицательной ф-и равен площади криволинейной трапеции.
Геометрический смысл определённого интеграла: определённый интеграл от неотрицательной ф-и равен площади криволинейной трапеции.
Площадь криволинейной трапеции. Пусть на отрезке [a;b] непрерывная функция y=f(x)≥0. Фигура, ограниченная сверху графиком функции, снизу – осью Ox, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.
Физический смысл определённого интеграла: работа переменной силы, величина которой есть непрерывная ф-я F=F(x), действующей на [a;b], равна определённому интегралу от величины F(x) силы, взятому по отрезку [a;b]. A= .
.
29. Формула Ньютона-Лейбница. Основные св-а определённого интеграла.
Пусть функция y=f(x) определена на отрезке [a;b].
Теорема: если ф-я y=f(x) непрерывна на отрезке [a;b] и F(x) – какая-либо её первообразная на [a;b], то имеет место формула: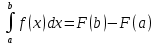 .
.
Основные св-а определённого интеграла
30. Методы вычисления определенного интеграла. Непосредственное вычисление. Интегрирование подстановкой.
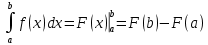
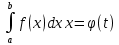 см далее
см далее
Теорема. Если функция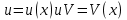 имеет непрерывные производные на отрезке [a; b], то имеет место формула
имеет непрерывные производные на отрезке [a; b], то имеет место формула 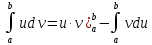
Пусть функция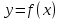 непрерывна на отрезке [-a;a] симметричном относительно точке X=0
непрерывна на отрезке [-a;a] симметричном относительно точке X=0
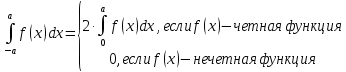
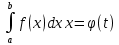
Теорема: если:
Замечание:
31. Интегрирование по частям. Интегрирование четных и нечетных функций в симметричных пределах.
Теорема. Если функция
 , знаменатель которой разложен на множители Q(x)= (x-x1)k1(x-x2)k2…(x2+p1x+q1)S1…( x2+pmx+qm)Sm можно представить и при том единственным образом в виде следующей суммы простейших дробей
, знаменатель которой разложен на множители Q(x)= (x-x1)k1(x-x2)k2…(x2+p1x+q1)S1…( x2+pmx+qm)Sm можно представить и при том единственным образом в виде следующей суммы простейших дробей 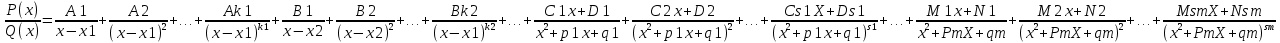
26. Интегрирование простейших рациональных дробей. Интегрирование рациональных дробей.
Простейших дробей:
Интегрирование рациональных дробей:
-
Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби. -
Разложить знаменатель правильной дроби на множители и представить её в виде суммы простейших рациональных дробей. -
Проинтегрировать многочлен и полученную сумму простейших дробей.
27. Интегрирование тригонометрических ф-й. Интегрирование иррациональных ф-й.
Универсальная тригонометрическая подстановка
R – знак рациональной функции.
Вычисление неопределённых интегралов типа
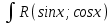 dx сводится к вычислению интегралов от рациональной функции подстановкой
dx сводится к вычислению интегралов от рациональной функции подстановкой 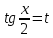 , которая называется универсальной.
, которая называется универсальной. Другие подстановки:
-
Если R(sinx;cosx) нечётная относительно sinx т.е. (R(-sinx;cosx)= -R(sinx;cosx)), то cosx=t -
Если R(sinx;cosx) нечётная относительно cosx, ( R(sinx;-cosx)= -R(sinx;cosx)), то sinx=t -
Если R(sinx;cosx) чётная относительно sinx и cosx, (R(-sinx;-cosx)= R(sinx;cosx)), то tgx=t.
Интегралы типа
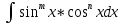
-
sinx=t, если n-целое положительное нечётное число -
cosx=t, если m- целое положительное нечётное число -
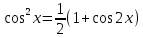 ,
, 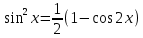 ,
,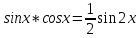 , если m и n – целые неотрицательные чётные числа
, если m и n – целые неотрицательные чётные числа -
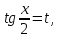 если m+n есть чётное целое отрицательное число
если m+n есть чётное целое отрицательное число
Использование тригонометрических преобразований
Интегралы типа
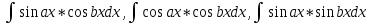
с помощью:
Интегрирование иррациональных функций
Интегралы типа
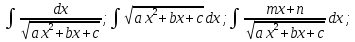 - неопределённые интегралы от иррациональных ф-й
- неопределённые интегралы от иррациональных ф-й -
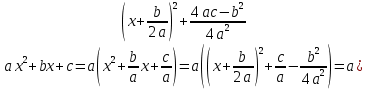 ,
, 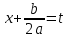 (выделяем полный квадрат, делаем замену)
(выделяем полный квадрат, делаем замену) -
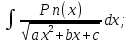 где Pn(x) – многочлен степени n
где Pn(x) – многочлен степени n -
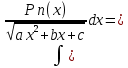 Qn-1(x)*
Qn-1(x)*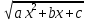 +λ
+λ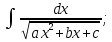
-
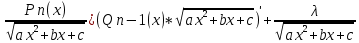
Тригонометрическая подстановка:
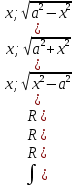 ,
, x=asint – для интегралов 1 типа, x=atgt – 2 типа, x=
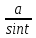 - 3 типа
- 3 типа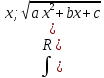 . Интегралы указанного вида приводятся к интегралам, которые можно вычислить с помощью соответствующих подстановок.
. Интегралы указанного вида приводятся к интегралам, которые можно вычислить с помощью соответствующих подстановок. 28. Определённый интеграл как предел интегральной суммы. Геометрический и физический смысл определённого интеграла.
28. Определённый интеграл как предел интегральной суммы. Геометрический и физический смысл определённого интеграла.Пусть ф-я y=f(x) определена на отрезке [a;b], a
-
С помощью точек x0=a, x1, x2,…, xn=b (x0n)
-
В каждом частичном отрезке [xi-1;xi], i=1,2,..,n выб. произвольная точка Сiϵ[xi-1;xi], вычислим f(Сi) -
Умножим найденное значение на длину отрезка: f(Сi)*∆х= f(Сi)*(xi -xi-1) -
Sn= f(С1)*∆х1+ f(С2)*∆х2+…+ f(Сn)*∆х=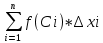 – интегральная сумма; λ=max∆хi – длина наибольшего частичного отрезка
– интегральная сумма; λ=max∆хi – длина наибольшего частичного отрезка -
Найдём предел интегральной суммы, когда n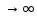 так, что λ
так, что λ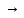 0. Если при этом интегральная сумма Sn имеет предел, который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число называется определённым интегралом от функции y=f(x) на отрезке [a;b] и обозначается
0. Если при этом интегральная сумма Sn имеет предел, который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число называется определённым интегралом от функции y=f(x) на отрезке [a;b] и обозначается 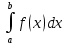 . Таким образом,
. Таким образом, 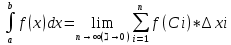 , a – верхний предел интегрирования, b – нижний, [a;b] – область интегрирования.
, a – верхний предел интегрирования, b – нижний, [a;b] – область интегрирования.
Теорема Коши (существования опр. Интеграла): если ф-я y=f(x) непрерывна на отрезке [a;b], то определённый интеграл существует. (достаточное условие)
 Геометрический смысл определённого интеграла: определённый интеграл от неотрицательной ф-и равен площади криволинейной трапеции.
Геометрический смысл определённого интеграла: определённый интеграл от неотрицательной ф-и равен площади криволинейной трапеции. Площадь криволинейной трапеции. Пусть на отрезке [a;b] непрерывная функция y=f(x)≥0. Фигура, ограниченная сверху графиком функции, снизу – осью Ox, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.
Физический смысл определённого интеграла: работа переменной силы, величина которой есть непрерывная ф-я F=F(x), действующей на [a;b], равна определённому интегралу от величины F(x) силы, взятому по отрезку [a;b]. A=
 .
.29. Формула Ньютона-Лейбница. Основные св-а определённого интеграла.
Пусть функция y=f(x) определена на отрезке [a;b].
Теорема: если ф-я y=f(x) непрерывна на отрезке [a;b] и F(x) – какая-либо её первообразная на [a;b], то имеет место формула:
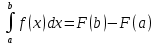 .
.Основные св-а определённого интеграла
-
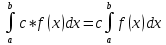
-
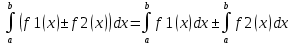
-
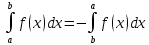
-
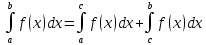 – св-о аддитивности
– св-о аддитивности -
Если ф-я F(x) непрерывна на [a;b], то существует т. Сϵ[a;b] такая, что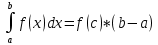 – теорема о среднем
– теорема о среднем -
Если ф-я F(x) сохраняет знак на [a;b], где a -
Неравенство между непрерывными ф-ми на [a;b] (a1(x)≤ f2(x) при xϵ[a;b], то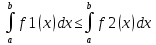
Оценка интеграла. Если m и M соответствуют наименьшее и наибольшее значение ф-и y=f(x) на отрезке [a;b], то m*(b-a)≤ ≤M*(b-a)
≤M*(b-a)
Модуль определённого интеграла не превосходит интеграла от модуля подынтегральной ф-и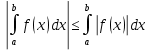 , a
, a
Производная определённого интеграла по переменному верхнему пределу равна подынтегральной ф-и, в которой переменная интегрирования заменена этим пределом.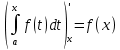
30. Методы вычисления определенного интеграла. Непосредственное вычисление. Интегрирование подстановкой.
-
Методы вычисления определенного интеграла:
-
Формулы Ньютона-Лейбница.
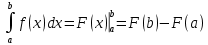
-
Интегрирование подстановкой
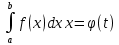 см далее
см далее-
Интегрирование по частям.
Теорема. Если функция
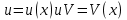 имеет непрерывные производные на отрезке [a; b], то имеет место формула
имеет непрерывные производные на отрезке [a; b], то имеет место формула 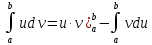
-
Интегрирования четных и нечетных функций в симметричных пределах Теорема
Пусть функция
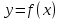 непрерывна на отрезке [-a;a] симметричном относительно точке X=0
непрерывна на отрезке [-a;a] симметричном относительно точке X=0 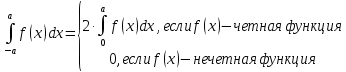
-
Непосредственное вычисление -
Интегрирование подстановкой.
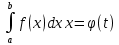
Теорема: если:
-
Функция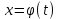 и
и 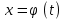 непрерывны при tє[α;β]
непрерывны при tє[α;β] -
Множеством значений функции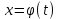 при tє[α;β] является [a;b]
при tє[α;β] является [a;b] -
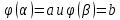 , то
, то 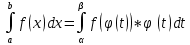
Замечание:
-
Возвращаться к старой переменной не требуется -
Вместо подстановки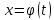 t=g(x)
t=g(x) -
Нельзя забывать менять пределы интегрирования при замене переменных
31. Интегрирование по частям. Интегрирование четных и нечетных функций в симметричных пределах.
-
Интегрирование по частям.
Теорема. Если функция