имеет непрерывные производные на отрезке [a; b], то имеет место формула

2. 
   Интегрирования четных и нечетных функций в симметричных пределах Теорема
   

Пусть функция непрерывна на отрезке [-a;a] симметричном относительно точке X=0



32. Интеграл с бесконечным промежутком интегрирования.

Пусть функция непрерывна на отрезке от [a;+ ). Если существует конечный предел 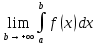, то его называют несобственным интегралом 1 рода и обозначают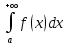

1. 
   Если предел существует, то интеграл сходится
   
2. 
   Если предел не существует или бесконечен, то интеграл расходится
   

Теорема 1 Признак сравнения

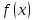Если на промежутке от [a;+ ) непрерывной функции   и удовлетворяет условиям 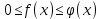, то из сходимости 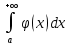следует сходимость 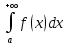, а из расходимости 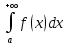следует расходимость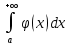

Теорема 2 Если существует предел при

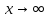
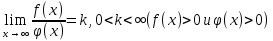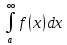, то и 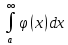оба сходятся или оба расходятся

33. Интеграл от разрывной функции.

---

Пусть функция непрерывна на промежутке [a; b) и имеет бесконечный разрыв при x=b. Если существует конечный предел 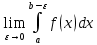, то его называют несобственным интегралом 2 рода;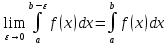



Если предел в правой части существует, то несобственный интеграл сходится, если не существует или равен бесконечности, то расходится.

Теорема 1

Пусть на промежутке [a, b) функции и непрерывны, при x=b терпят бесконечный разрыв и удовлетворяют условию . Из сходимости интеграла 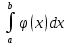вытекает сходимость интеграла , а из расходимости следует расходимость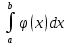

Теорема 2

Пусть функция и непрерывны на промежутке [a, b) и в точке x=b терпят разрыв. Если существует предел 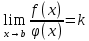, 0 , то и 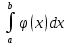одновременно сходятся или расходятся.
34. Схемы применения определенного интеграла. Вычисление площадей плоских фигур.

1. 
   Схемы применения определенного интеграла:
   

1. 
   Схема (метод интегральных сумм) Базируется на определении определенного интеграла
   

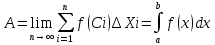
Метод сумм основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.

---

2. 
   Схема (Метод дифференциала или Метод отбрасывания бесконечно малых высших порядков)
   

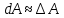при

2. 
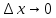
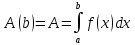
   Вычисление площадей плоских фигур
   

1. 
   Прямоугольные координаты
   

Криволинейная трапеция выше оси Ox S=

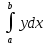
Криволинейная трапеция ниже оси Ox S= -

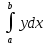
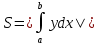- в общем случае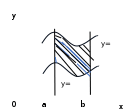











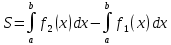
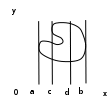
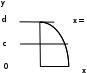
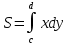
Если криволинейная трапеция ограничена кривой, заданной параметрически, ограничена прямыми x=a и x=b, и осью Ox, то площадь ищем:

2. 
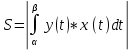
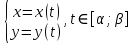
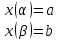
   Полярные координаты
   

Площадь криволинейного сектора, то есть плоской фигуры, ограниченной непрерывной линией 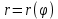с двумя лучами f=α и f=β, где α<β, где r и полярные координаты.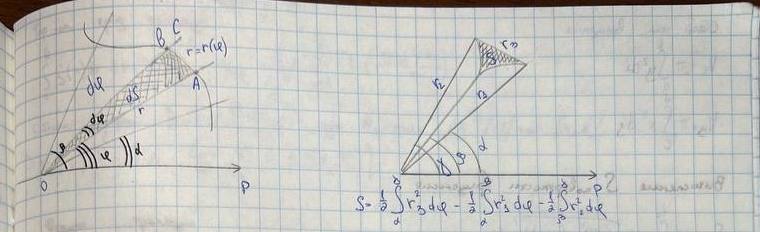

---

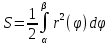
35. Вычисление длины дуги плоской кривой. Вычисление объема тела.

1. 
   Вычисление длины дуги плоской кривой
   

Под длиной дуги AB понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина найденного звена стремится к нулю. AB имеет длину

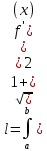
Если кривая AB задана в параметрической форме

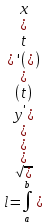
Равенство d 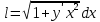называется формулой дифференциала дуги в прямоуг. координатах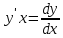





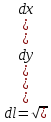
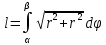– полярные координаты

2. 
   Вычисление объема тела
   

Формула объема тела по S паралл. cечений

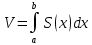
Объем тела вращения: 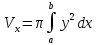(вдоль Ох); 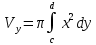(вдоль Оу)

36. Формула прямоугольников. Формула трапеций. Формула парабол.

1. 
   Формула прямоугольников
   
2. 
   Формула трапеции
   

…

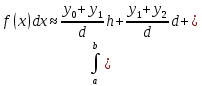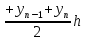
Или


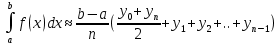
|R_n| 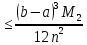, где M₂=Max | 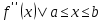– абсолютная погрешность

Формула параболы

…

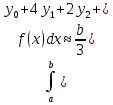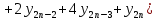
Или

… …+

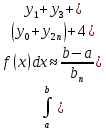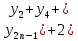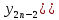
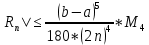| , где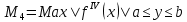

---

– абсолютная погрешность

37. Основные понятия рядов. Ряд геометрической прогрессии.

1. 
   Основные понятия рядов
   

Числовым рядом называется выражение вида 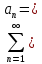a1+a2+…+an+…, где: a1, a2, … an, … - члены ряда. An-общий член ряда

Сумма первых n членов ряда называется n-й частичной суммой ряда: 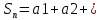…+an

Частичные суммы: S1=a1; S2=a1+a2; S3=a1+a2+a3

Сумма ряда: S=

• 
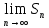
  Если конечный предел последовательности частичных сумм ряда существует, то ряд сходится
  
• 
  Если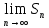 не существует или 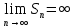, то ряд называется расходящимся. Такой ряд суммы не имеет.
  

Ряд геометрической прогрессии

a+aq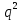+a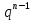 +…+a +…(a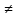 0) (4)

Сумма первых n членов прогрессии находится по формуле:

• 
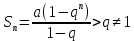
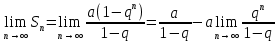
  При |q| <1 сходится;
  
• 
  При |q|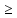 1 расходится
  

1. 
   Если |q| <1, то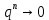 при 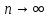. Поэтому 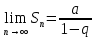, ряд (4) сходится, его сумма равна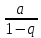
   
2. 
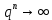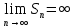   Если |q|>1, то при n . Поэтому , ряд (4) расходится
   
3. 
   Если |q|=1, то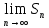 не существует и ряд расходится.
   

38. Необходимый признак сходимости числового ряда.

---

Смотрите также файлы

• Роль личности в истории. М. Тэтчер.docx

• МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ.docx

• Архитектура персонального компьютера.docx

• Автоматическая телефонная станция.docx

• Требования к реферату.docx