Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 177
Скачиваний: 3
СОДЕРЖАНИЕ
Глава 1. Понятия об основных алгебраических структурах.
§1. Алгебры. Подалгебры. Гомоморфизмы алгебр.
§3. Подгруппа. Достаточные условия подгруппы.
Глава 2. Матрицы и определители.
§1.Матрицы. Группа и кольцо матриц.
§2. Определители, их свойства.
Глава 3. Системы линейных уравнений, методы их решения.
Глава 5. Теория делимости в кольце Z.
§1. Отношение делимости в Z и его свойства.
§3. Взаимно простые числа и их свойства.
§4. НОК целых чисел и его свойства.
§5. Простые числа и их свойства.
Глава 6. Теория делимости в кольце Р[х].
§2. Отношение делимости в кольце Р[х] и его свойства.
Свойства отношения делимости в кольце Р[x].
§3. Деление с остатком в кольце P[x].
§4. Приводимые и неприводимые многочлены
§2. Группа. Аксиомы группы.
Все алгебры можно классифицировать с точки зрения свойств операций, заданных на множествах-носителях. Эта классификация позволяет выделить из множества алгебр алгебры определенного рода, которые будут одинаковы, с точностью до изоморфизма.
Прежде, чем давать определения различных родов алгебр, договоримся о терминологии. Если задана бинарная алгебраическая операция на множестве А, то в зависимости от того, какая задана операция и как она обозначена, будем говорить и писать:
| В общей терминологии | В аддитивной терминологии | В мультипликатив-ной терминологии |
| Операция * | Сложение + | Умножение • |
| Результат a * b | Сумма a + b | Произведение a • b |
| Нейтральный элемент е | Нуль 0 | Единица 1 |
| Симметричный элемент a' | Противополож-ный элемент -a | Обратный элемент a-1 |
Определение 1. Алгебра <А, *> с одной бинарной операцией называется группоидом.
Например,
- группоиды, a, , . - не являются группоидами.
Определение 2. Полугруппой называется алгебра <А, *> с бинарной ассоциативной операцией:
a,b,c А, (а*b)*с = а*(b*с). Можно сказать, что полугруппа - это ассоциативный группоид.
Например, N, •>. Z, +>, Q, +> - полугруппы, так как операции сложения и умножения на множествах N, Z, Q - ассоциативны. Алгебры, не являются полугруппами.
Определение 3. Моноидом называется алгебра <А, *>, бинарная операция которой удовлетворяет условиям:
1) a,b,c А, (а*b)*с = а*(b*с) - операция ассоциативна,
2) е А | a A, е*а = а*е = а - существует нейтральный элемент.
Можно сказать, что моноид - это полугруппа с нейтральным элементом.
Например,- является моноидом, так как е = 1, 1 Z, a не является моноидом, так как е=0, 0N.
Определение 4. Группойназывается алгебра, бинарная операция которой удовлетворяет условиям, называемым также аксиомами группы:
Аl. " a,b,cÎ G, (a*b)*c = a*(b*c) (ассоциативность);
А2. е G | aG, e*a = a*e = а (существование нейтрального элемента);
A3. " a Î G, a' G | a*a' = a'*a = e (симметризуемость каждого элемента).
Из определения видно, что любая группа является полугруппой и моноидом. Можно сказать, что группа - это моноид, каждый элемент которого имеет симметричный элемент.
В некоторых случаях, удобно использовать следующее определение группы:
Определение 4*. Алгебрас бинарной операцией * называется группой, если выполняются следующие условия:
а) " a,b,c Î G, (a*b)*c = a*(b*c).
б) " a,b Î G, каждое из уравнений а*х = b и у*а = b имеет хотя бы одно решение.
Первое определение группы более удобно для проверки того факта, будет ли данная алгебра группой. Второе определение характеризует группу как алгебру, в которой разрешимы уравнения первой степени. Можно доказать, что определения 4 и 4* равносильны. В определении группы заложен алгоритм решения всех задач, связанных с выяснением вопроса - будет ли данная алгебра группой.
Определение 5. Группаназывается коммутативной (или абелевой), если операция * коммутативна, т.е. выполняется аксиома:
А4. " a,b Î G, a*b = b*a (коммутативность).
Указание. Для доказательства того, что множество А с операцией * является группой, нужно.
во-первых, показать, что операция * является бинарной операцией на множестве А, т.е. выполнимой и однозначной операцией ранга 2 на А,
во-вторых, проверить выполнимость аксиом A1, A2, A3 группы для алгебры <А, *>.
Если первое из этих условий не выполняется, то нет смысла в проверке аксиом.
Пример 1. Рассмотрим множество Z целых чисел относительно операции сложения. Покажем, что- абелева группа.
а) Операция + является выполнимой на Z, так как " a,bÎZ, (a+b)Z; однозначной на Z, так как результат (а + b) определяется однозначно. Ранг операции "+" равен двум, так как в определении операции используется пара элементов (а, b) (а + b). Следовательно,- группоид.
б) Операция "+" ассоциативна на Z, так как " a,b,cÎ Z,
(а+b)+с = а+(b +с). Следовательно,- полугруппа.
в) Роль нейтрального элемента будет играть число 0, так как
" a Î Z, а + 0 = 0 + а = а. Следовательно,- моноид.
г) Для всякого целого числа существует противоположное число: " aÎZ, (-а) | а + (-а) = (-а) - а = 0.
Следовательно,- группа.
д) Операция + коммутативна на Z, так как " a,b Î Z, a + b = b + a.
Таким образом,- коммутативная группа. Ее обычно называют аддитивной группой целых чисел.
Пример 2. Рассмотрим множество Z относительно операции умножения целых чисел. Выясним, алгеброй какого рода является пара:
а) Умножение является бинарной операцией на Z, выполнимой и однозначной. Следовательно,- группоид.
б) Операция умножения на Z ассоциативна, т.е. " a,b,cÎZ,
a(bc) = (ab)c. Следовательно,- полугруппа.
в) Число 1 является нейтральным элементом относительно операции умножения, так как " a Î Z, 1 • а = а 1 = а. Значит,- моноид.
г) Теперь осталось проверить аксиому существования симметричного элемента на Z относительно операции умножения. Очевидно, что все целые числа, кроме 1 и -1, не имеют обратных элементов на Z, то есть аксиома A3 не выполняется.
Следовательно,- группой не является. Можно также показать, что уравнения ах = b, уа = b разрешимы не для всех целых чисел.
Пример 3. Выясним, будет ли группой множество Q0 рациональных чисел без нуля относительно бинарной операции умножения рациональных чисел.
а) Очевидно, что умножение рациональных чисел является бинарной операцией на Q, выполнимой и однозначной. Следовательно, < Q0, •> -группоид.
б) Операция умножения - ассоциативна. Следовательно,
< Q0, •> -полугруппа.
в) Нейтральный элемент равен 1. Следовательно, < Q0, •> - моноид.
г) Кроме того, " aÎ Q0, а-1Q0 | а • а-1 = а-1• а = 1.
Итак, < Q0. •> - группа. Ее обычно называют мультипликативной группой рациональных чисел. Очевидно, что группа
< Q0, •> - абелева.
Определение 6. Группуназывают бесконечной, если G -бесконечное множество.
Пример 4. Пусть {к} - множество целочисленных степеней некоторого целого числа а. Тогда <{к}, •> - бесконечная мультипликативная группа.
Проверьте самостоятельно!
Определение 7. Группуназывают конечной, если G -конечное множество. Число элементов множества G называют порядком группы и обозначают |G| (или 0r, или (G: 1)).
Пример 5. Рассмотрим пример конечной группы. Пусть дано множество Z и натуральное число m. Будем делить все целые числа на m. Числа, которые при делении на m будут иметь одинаковые остатки, соберем в один класс. Так как различных остатков будет m (0, 1, 2, ... , m-1), то и различных классов тоже будет m {}.
Обозначим это множество классов символом Zm и зададим на этом множестве операцию сложения классов по правилу:=
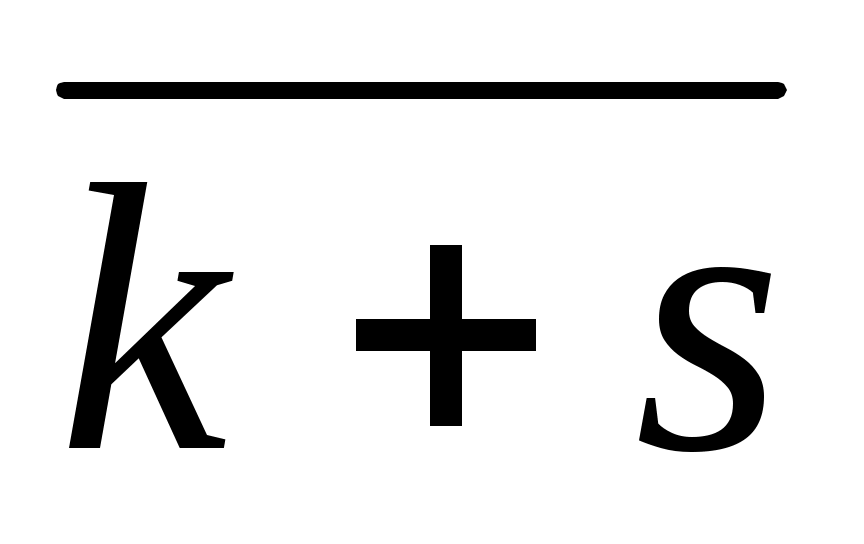
Тогдаm, > - будет конечной группой. Докажите это самостоятельно!
Пример 6. Доказать, что0, •>, где р - простое число и =
будет тоже группой.
1 2 3 4 5 6 7 8 9 ... 16
§3. Подгруппа. Достаточные условия подгруппы.
Определение 1. Пусть
Если Н - подгруппа группы G, то пишут Н < G.
Замечание. Для того, чтобы выяснить, является ли некоторое множество HG подгруппой группы G относительно операции *, заданной на G, достаточно проверить следующие условия:
а) а Н, b Н, а * b H - условие замкнутости,
б) а Н, а' Н - условие симметризуемости,
называемые в дальнейшем достаточными условиями подгруппы.
Действительно, если а Н, а' Н, то а * а'Н. Так как а * а' = е, то нейтральный элемент е группы G также принадлежит и множеству Н. Операция * на множестве Н является ассоциативной, так как она ассоциативна на множестве G, включающем Н. Итак, <Н, *> - группа.
Пример 1. Рассмотрим аддитивные группы чисел
,. Имеет место следующая цепочка 2Z
Покажем, например, что 2Z
а) a, b 2Z, a + b 2Z,
б) a 2Z, -a 2Z.
Таким образом, достаточные условия подгруппы выполнены.
Аксиома нейтрального элемента выполнима на 2Z, так как из условий а) и б) следует, что а + (- а) = 0, 02Z. Аксиома ассоциативности тоже выполнима, так как 2ZZ. Таким образом, 2Z < Z.
Пример 2. Подгруппами абстрактной группы G будут так называемые тривиальные подгруппы - сама группа G, т е G
Пример 3. Показать, что алгебра+, +> не является подгруппой аддитивной группы .
Действительно, R+ R. Кроме того,
а) a, b R+. (a + b)R+. - условие замкнутости выполнено,
б) aR+ -aR+, - условие симметризуемости не выполняется на R+. Следовательно, алгебра < R+ , +> не является подгруппой группы R,+>.§4. Кольцо, поле, линейное пространство.
Определение 1. Алгебра <А, +, •> - называется кольцом, если бинарные операции +, • удовлетворяют условиям:
1 -4) <А, +> - коммутативная группа
5) " a, b, c Î A, a • (b + c) = ab + ас
(b + с) • а = bа + са
Из определения следует, что любое кольцо - это коммутативная группа, в которой операция сложения связана с операцией умножения левым и правым дистрибутивными законами. На операцию умножения в общем случае никаких ограничений не накладывается. Если операция умножения дополнительно обладает свойствами коммутативности, ассоциативности и нейтральным элементом, то кольцо называют ассоциативно - коммутативным кольцом с единицей.
Пример 1., ,, m, +, •> - коммутативные кольца.
Определение 2. Алгебра <А, +, • > называется полем, если бинарные операции сложения и умножения удовлетворяют условиям (аксиомам):
1 -4) < А, +> - коммутативная группа
5-8) <А\{0}, •> - коммутативная группа
9)" a, b, c Î A, a • (b + c) = ab + ас
(b +с) • а = bа + са
Из определения следует, что любое поле - это аддитивная и мультипликативная группа одновременно, а также коммутативно-ассоциативное кольцо с единицей, в котором каждый ненулевой элемент обратим.
Пример 2.,, P, +, • > - поля.
Пусть дано не пустое множество V и поле F.
Элементы множества V будем обозначать малыми буквами латинского алфавита и называть векторами. Элементы поля F будем обозначать малыми буквами греческого алфавита и называть скалярами.
Определим на множестве V бинарную операцию сложения векторов : VVV, + а + b
и внешнюю композицию w: F•VV
w:<,а> а (умножение вектора на скаляр),
которую при фиксированном значении скаляра можно считать унарной операцией на множестве V.
Определение 3. Алгебраназывается линейным векторным пространством относительно операции сложения векторов и умножения вектора на скаляр, если 1-4) - коммутативная группа.
5) a, b V F, (а+b) = а + b
6) , F a V, (+) • a = a + a
7) , F a V, ( • ) • a = a • (b • a)
8) " a Î V, la = a
Из определения следует, что любое линейное векторное пространство является аддитивной коммутативной группой.
Примеры 3.n, + {wl | R}> - арифметическое линейное векторное пространство. 
Роль векторов в этом пространстве играют арифметические векторы вида: a =(1 ,2, ...,n)
Операция - это операция сложения таких векторов, операция wl -это операция умножения арифметического вектора на действительное число. Легко проверить, что эти операции удовлетворяют условиям 1-8. Покажем, например, чтоn, +> - коммутативная группа.
1. Так как операция + по определению является бинарной операцией на Rn, то < Rn , +> - алгебра.
2. a, b Rn, a + b = b + a
Действительно, пусть a =(1 ,2, ...,n), b = (1 2, ... ,n)
Тогда а+b=(a1+1,a2 +2, ...,an +n), b+a=(1+a1 ,2+a2, ...,n+an)
Так как операция сложения действительных чисел коммутативна, то a+b=b+a
3. " a, b, cÎ Rn, (a+b)+c=a+(b+c) проверяется аналогично.
4. Роль нуля будет играть вектор =(0,0 .. 0).
5. " a ÎV -а : а + (- а) = (-а) + а = действительно, если a =(a1 ,a2, ...,an), то -a =(-a1 ,-a2, ...,-an), которые в сумме дадут нулевой вектор.
Итак,n, +> - коммутативная группа. Остальные условия в определении линейного пространства проверить самостоятельно.
Замечание. Линейные пространства1, + {w | R}>, 2, +{w | R}>, <R3,+{w | R}> имеют наглядную геометрическую интерпретацию: 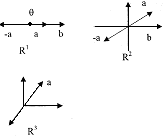
R1 - множество радиусов-векторов на прямой;
R2 - множество радиусов-векторов на плоскости;
R3 - множество радиусов-векторов в пространстве.
Глава 2. Матрицы и определители.
Перечень основных знаний и умений по данной теме:
- знать, какие операции определяются на множестве Mmn(R), при каких условиях они выполнимы:
- знать основные свойства операций, определенных на множестве Mmn(R);
- знать и уметь выполнять алгоритм каждой операции;
- уметь решать матричные уравнения;
- знать определение детерминанта n-го порядка, понимать структуру этого определения;
- знать основные свойства определителя;
- уметь записать разложение определителя порядка n = 2, n = 3, n = 4:
- знать и уметь пользоваться правилом Саррюса;
- уметь приводить определитель любого порядка с помощью элементарных преобразований к «треугольному виду» и вычислять его.
§1.Матрицы. Группа и кольцо матриц.
Пусть дано поле R. тогда таблицу вида:
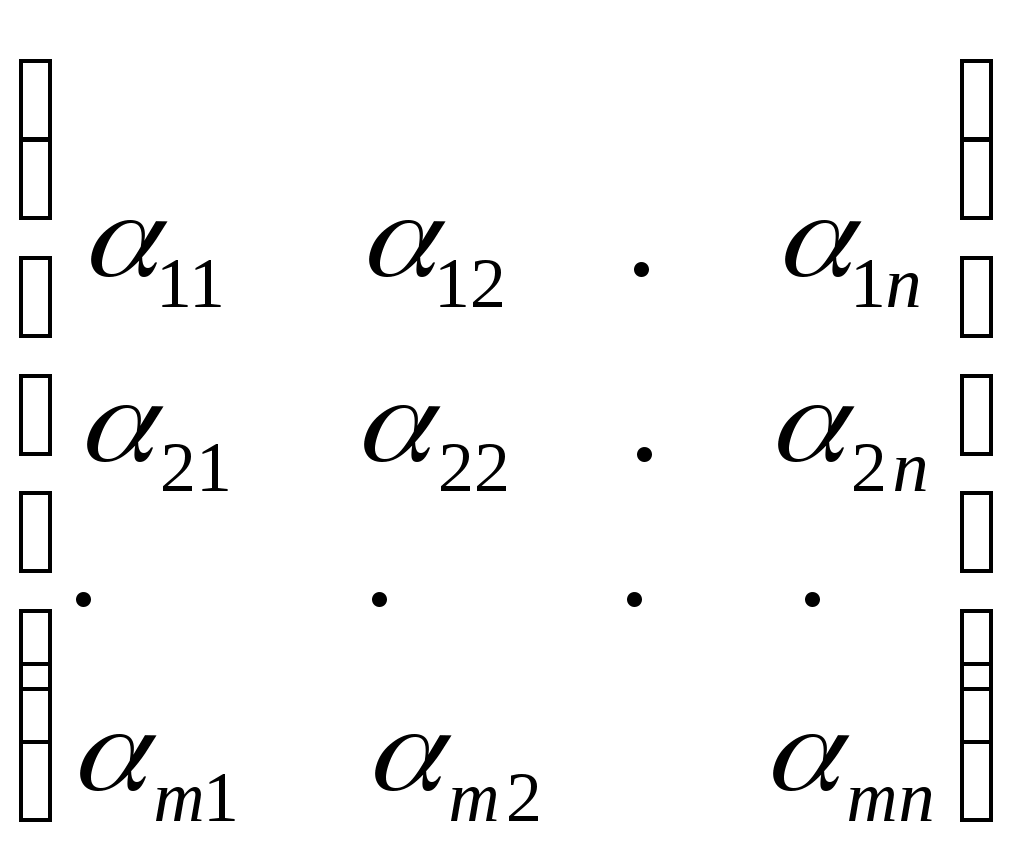 , где ik R, называют матрицей порядка mn и обозначают короче ||ik || i = 1, 2, ..., n, k = 1, 2, ...,m или буквами А, В, С, ...
, где ik R, называют матрицей порядка mn и обозначают короче ||ik || i = 1, 2, ..., n, k = 1, 2, ...,m или буквами А, В, С, ...Любая строка этой матрицы есть n-мерный арифметический вектор, а любой столбец - m-мерный арифметический вектор.
Всю матрицу можно рассматривать как mn -мерный вектор.
Множество всех матриц с элементами из поля R принято обозначать символом Mmn(R). На некоторых подмножествах этого множества можно определить две бинарные операции (+, ) и две унарные операции (умножение матрицы на скаляр и нахождение обратной матрицы).
Операция сложения матриц определяется только для тех матриц из множества Mnm(R), которые имеют одинаковый порядок, т.е. одинаковое число строк и столбцов.
Если A = ||ik || и В=||ik ||, то А + В = С = ||ik + ik || i = 1, 2,... m, k= 1,2,...,n
Например, матрицы порядка 23
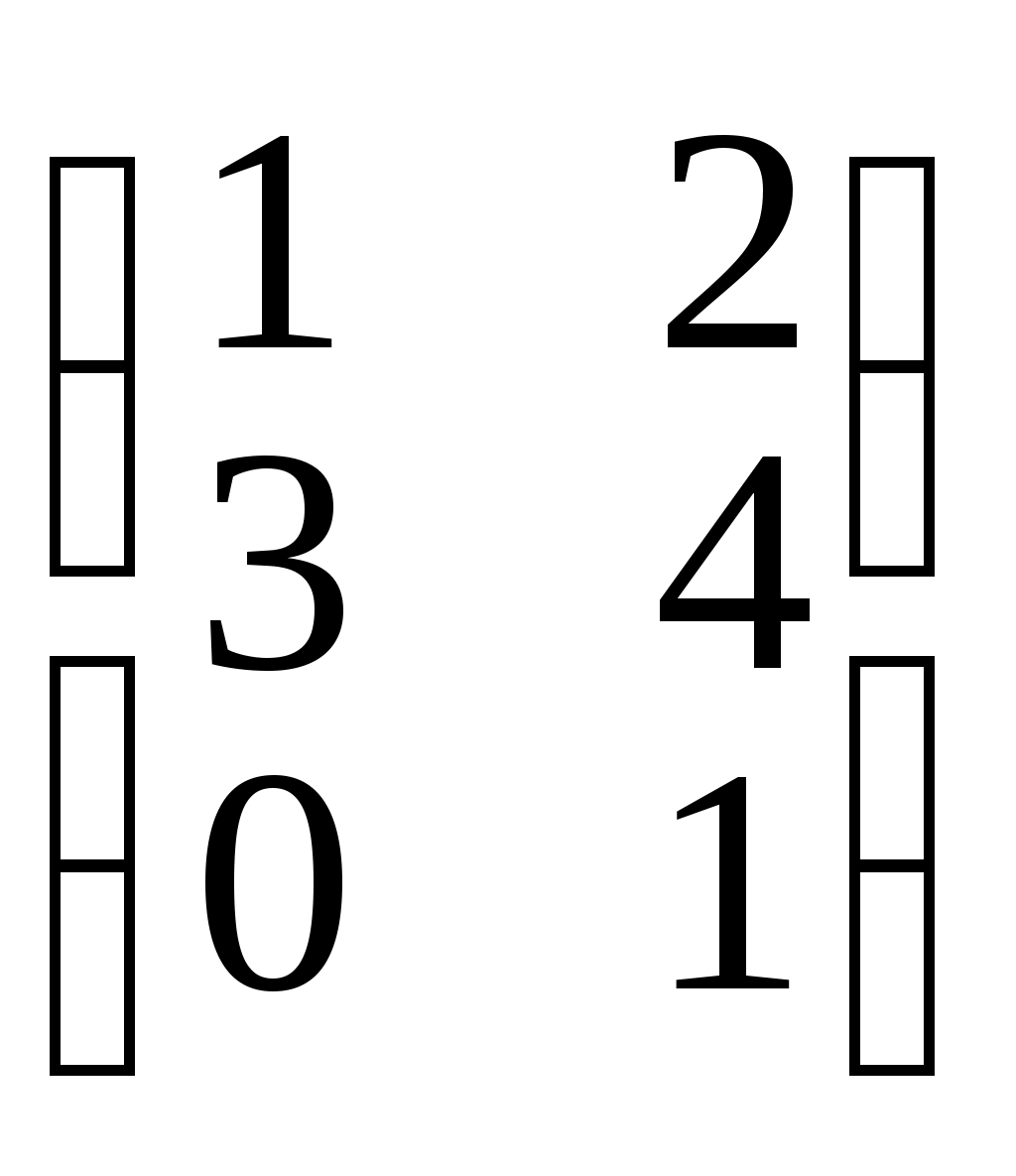 и (1 3 4 5) сложить нельзя, т.к. они имеют различный порядок.
и (1 3 4 5) сложить нельзя, т.к. они имеют различный порядок.
Операция умножения матриц определяется только для тех матриц из множества Mmn(R), порядки которых удовлетворяют следующему требованию: число столбцов первой матрицы должно совпадать с числом строк второй матрицы.
То есть, если матрица А имеет порядок mn, то матрица В в произведении А В должна иметь порядок ns .
Тогда А • В = С = ||Cik ||. где Cik находится по правилу: i-ая строка матрицы А умножается на k-ый столбец матрицы В (в смысле скалярного произведения).
Например, если А =
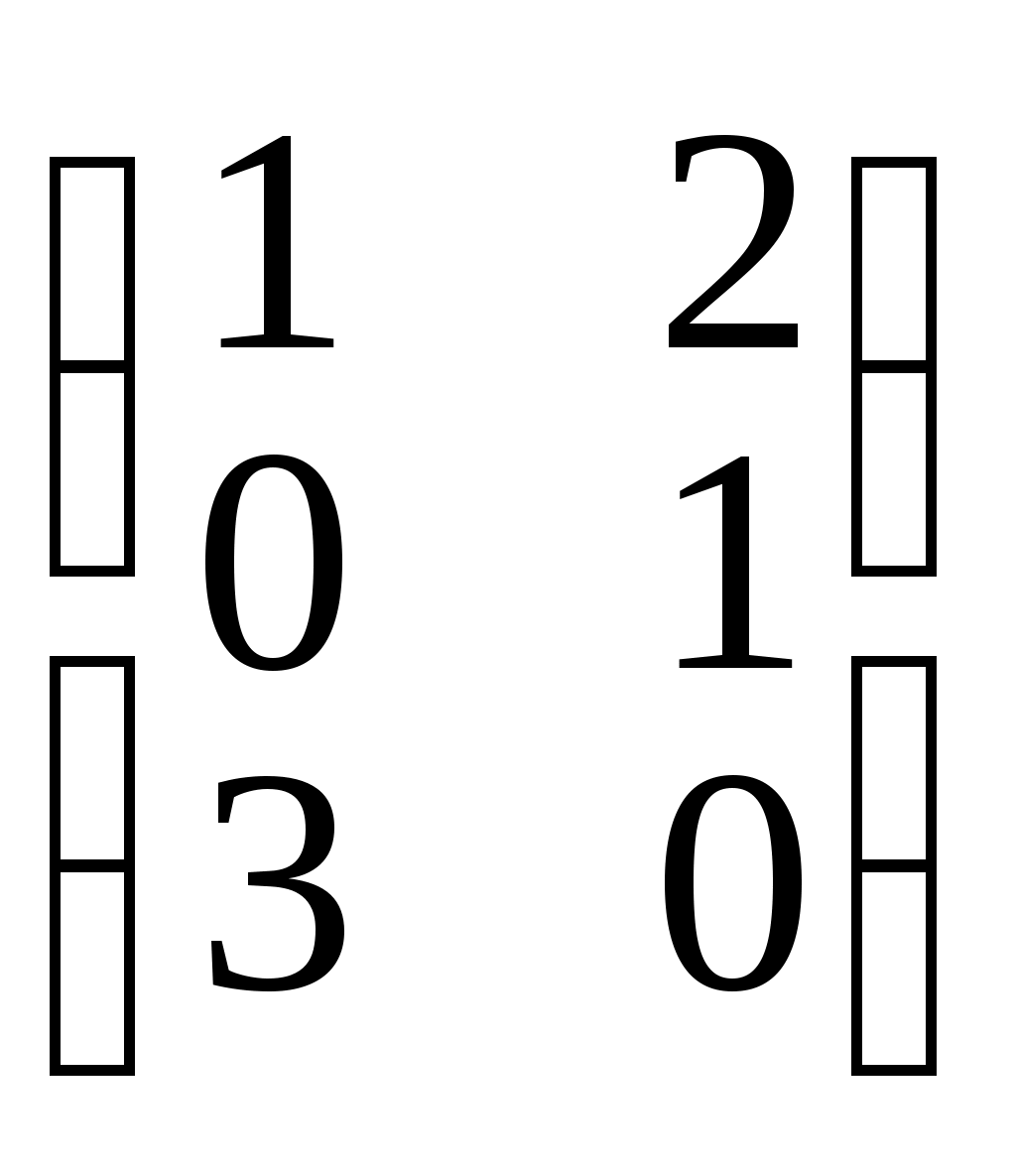 , то произведение А • В = С =
, то произведение А • В = С =Найдем произведение В • А, это тоже можно сделать, так как число столбцов матрицы В совпадает с числом строк
матрицы А
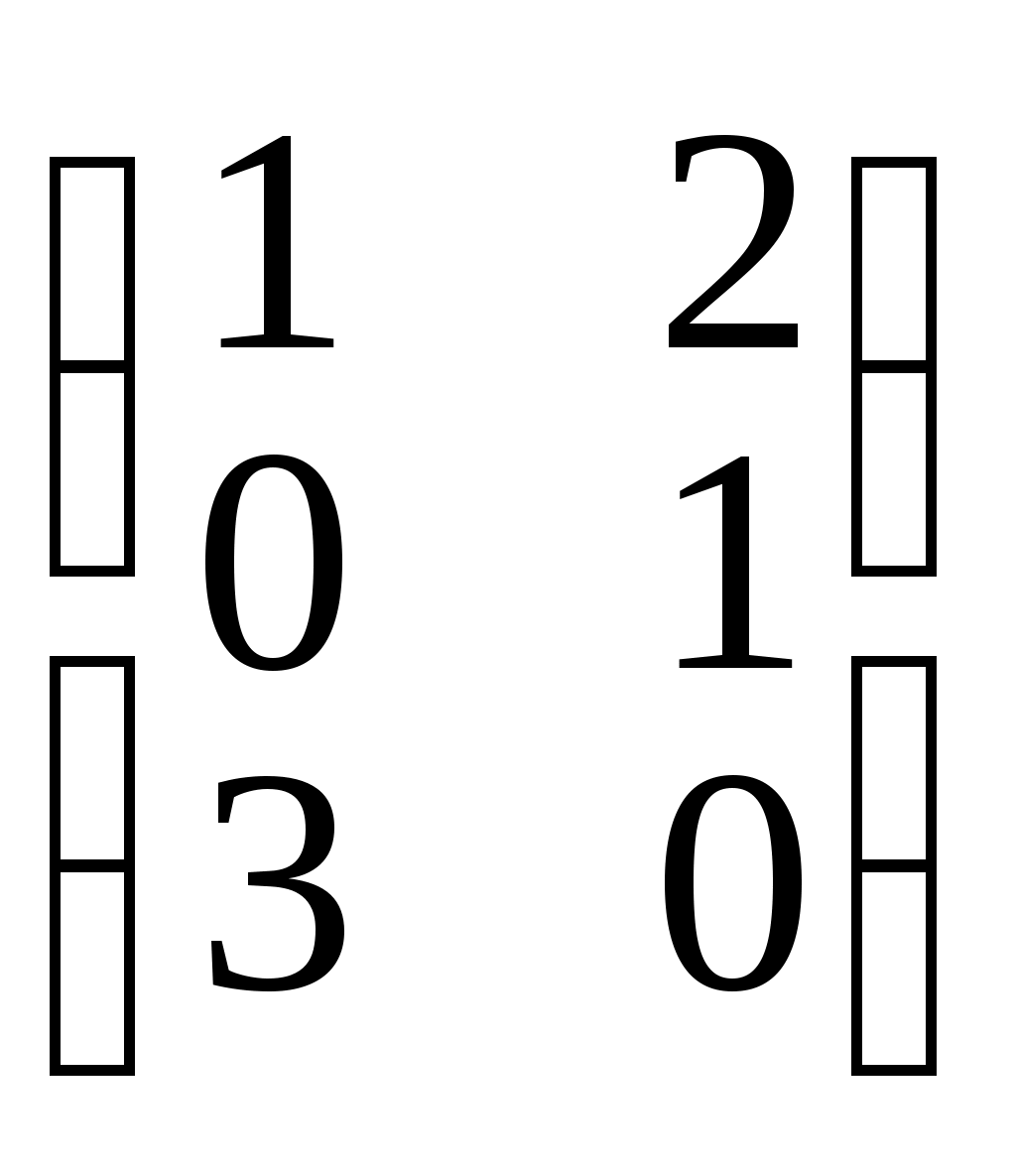 •
•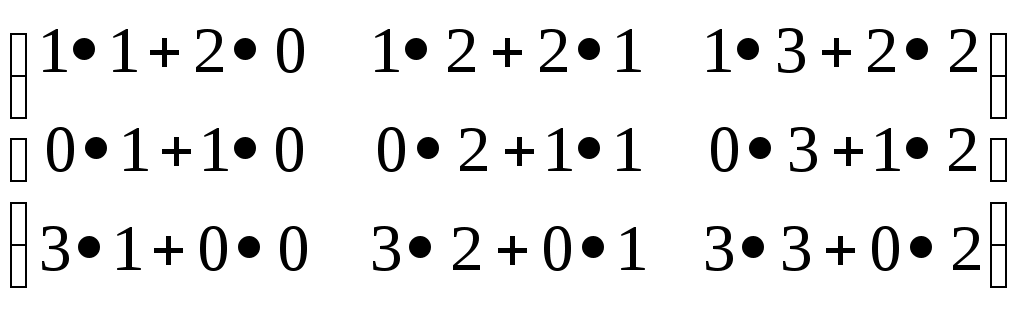 = =
= =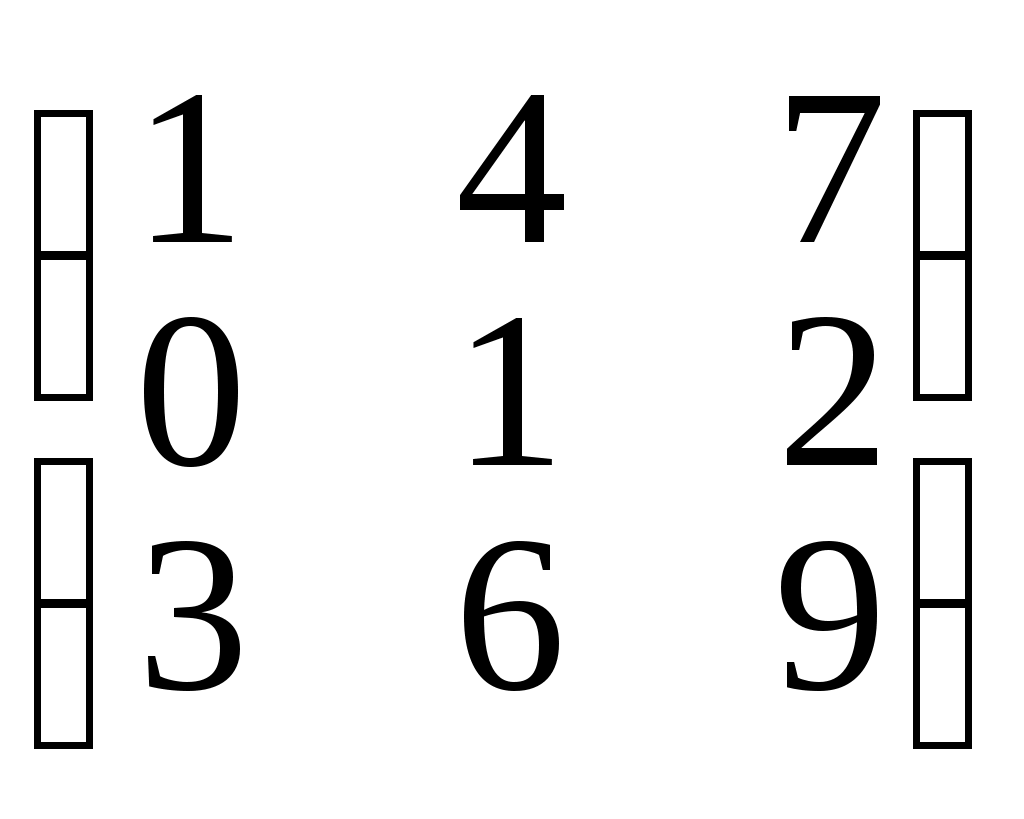
Замечания:
1. Как видим, А•В В•А, то есть операция умножения матриц некоммутативна.
2. Порядок матрицы А•В связан с порядками матриц А и В, матрица А•В имеет столько же строк, сколько и матрица А и столько же столбцов, сколько их имеет матрица В.
Матрицы
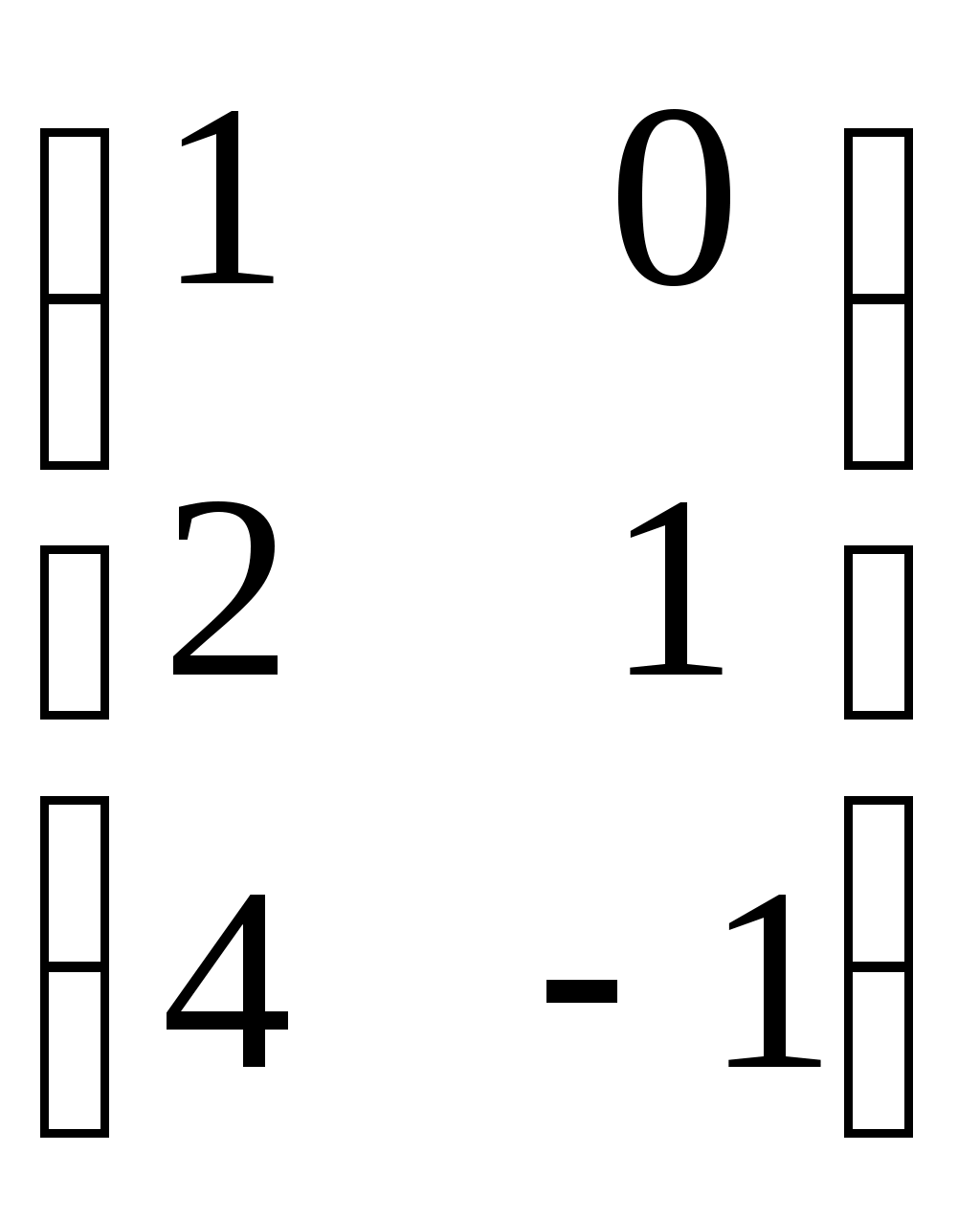 перемножить нельзя, так как их порядки не удовлетворяют требуемому условию.
перемножить нельзя, так как их порядки не удовлетворяют требуемому условию.Операция умножения на скаляр определяется на всем множестве Mmn(R) без ограничений: ||ik ||=||ik ||
Пример 1: 3•
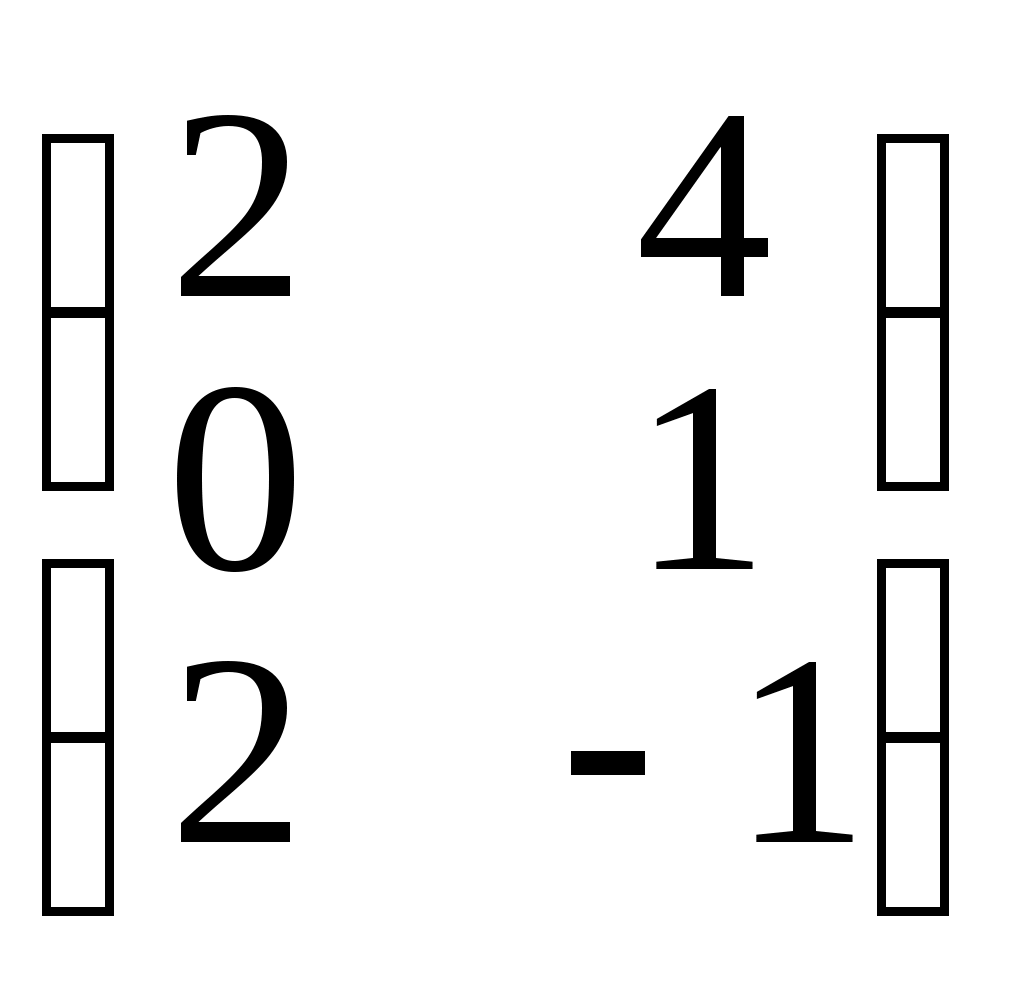 =
= 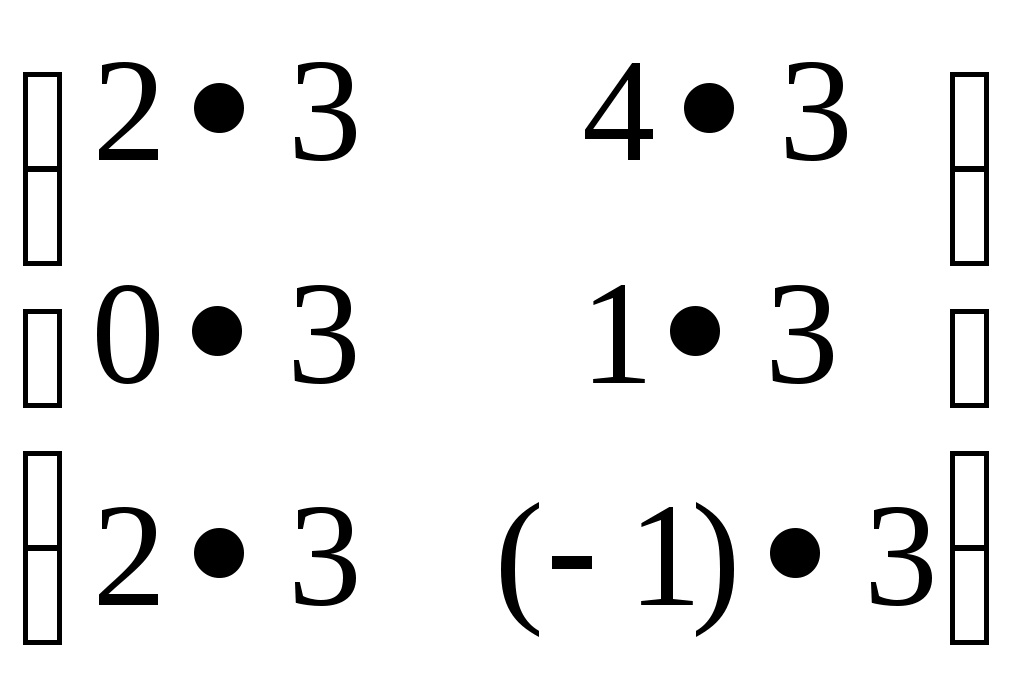 =
= 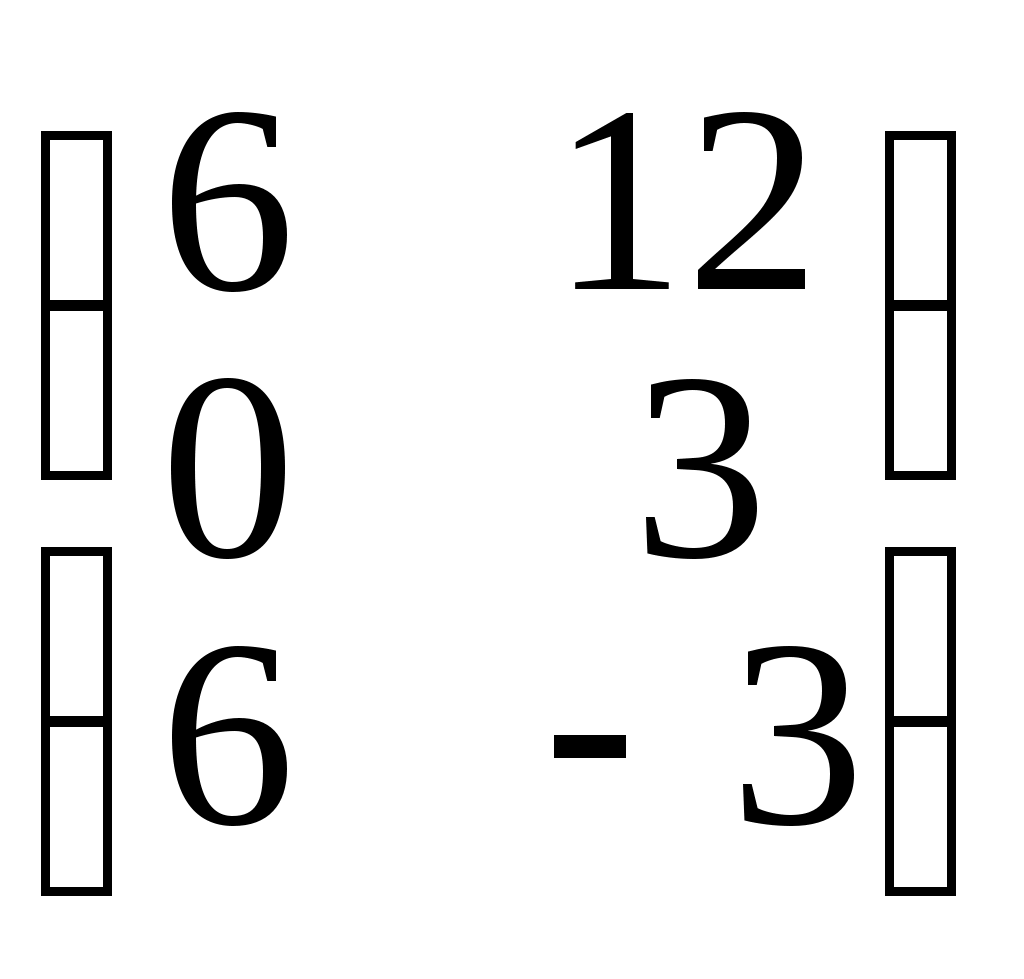
Определение 1. Нулевой матрицей называется квадратная матрица вида:
0 =
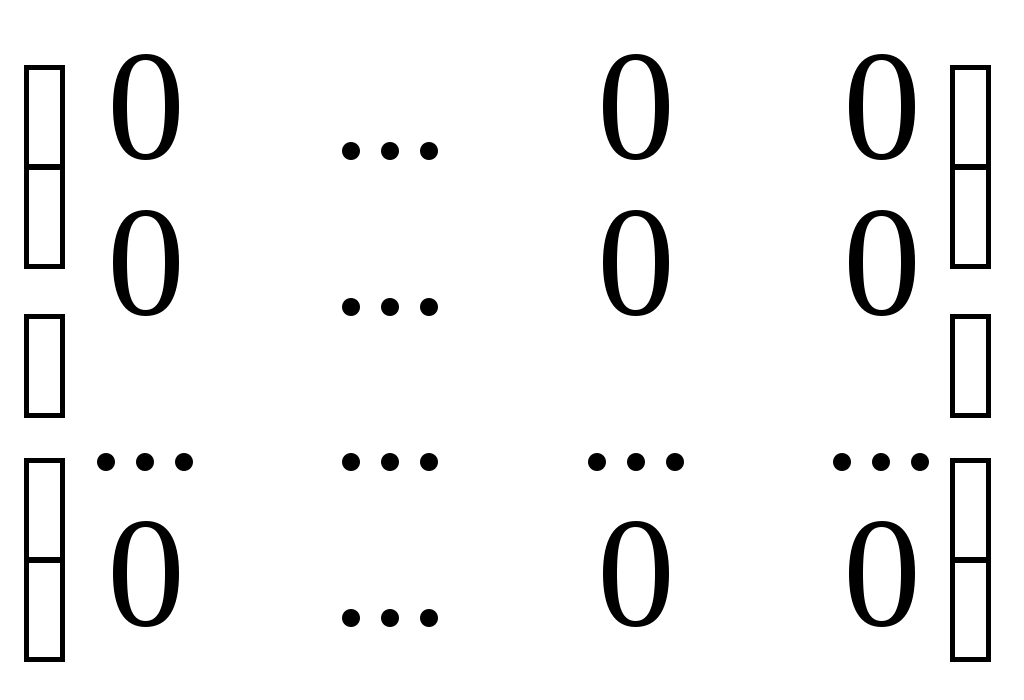
, у которой все элементы равны нулю.
Проверьте самостоятельно, что если матрицы А и 0 одного порядка, то А+0 = 0+А = А т.е. матрица 0 играет роль нейтрального элемента на множестве Mmn(R), относительно операции сложения.
Определение 2. Матрица (-А) называется противоположной матрице А, если (-А) + А=А+(-А) = 0
Самостоятельно проверьте, что для матрицы А =
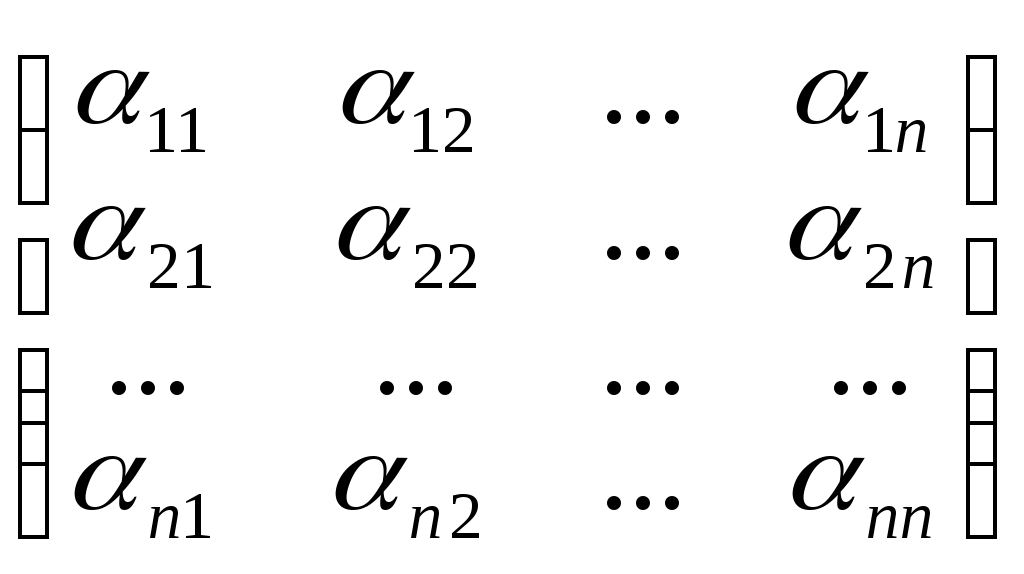 -А=
-А= 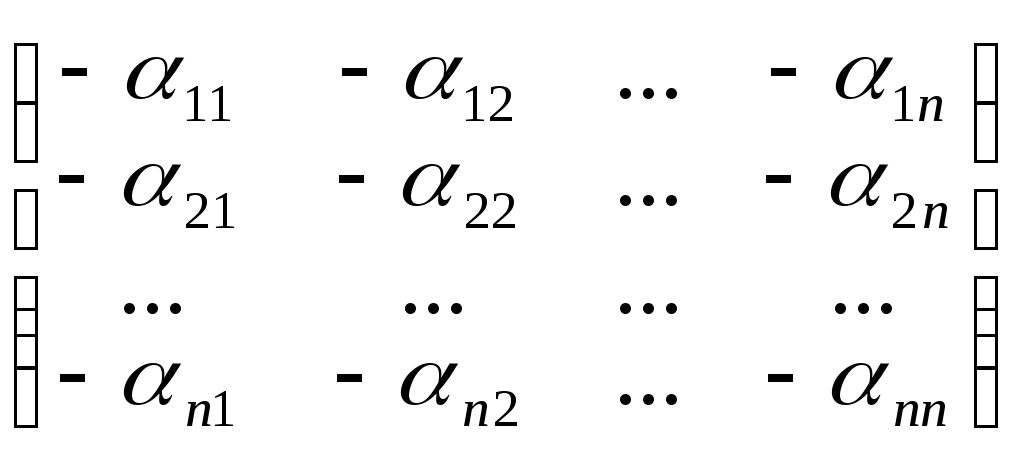
Теорема 1. Алгебра
Схема доказательства:
1. Множество Mnn(R) замкнуто относительно операции сложения матриц, т.к. A, B Mnn(R), (A+B=C) Mnn(R) (смотри определение операции +).
2. A, B, C Mnn(R), (A+B)+C = А+(В+С) т.к. операция сложения матриц определяется через операцию сложения действительных чисел, которая ассоциативна.
3. A, B Mnn(R), А+В = В+А, т.к. операция сложения действительных чисел коммутативна.
4. нулевая матрица 0 =
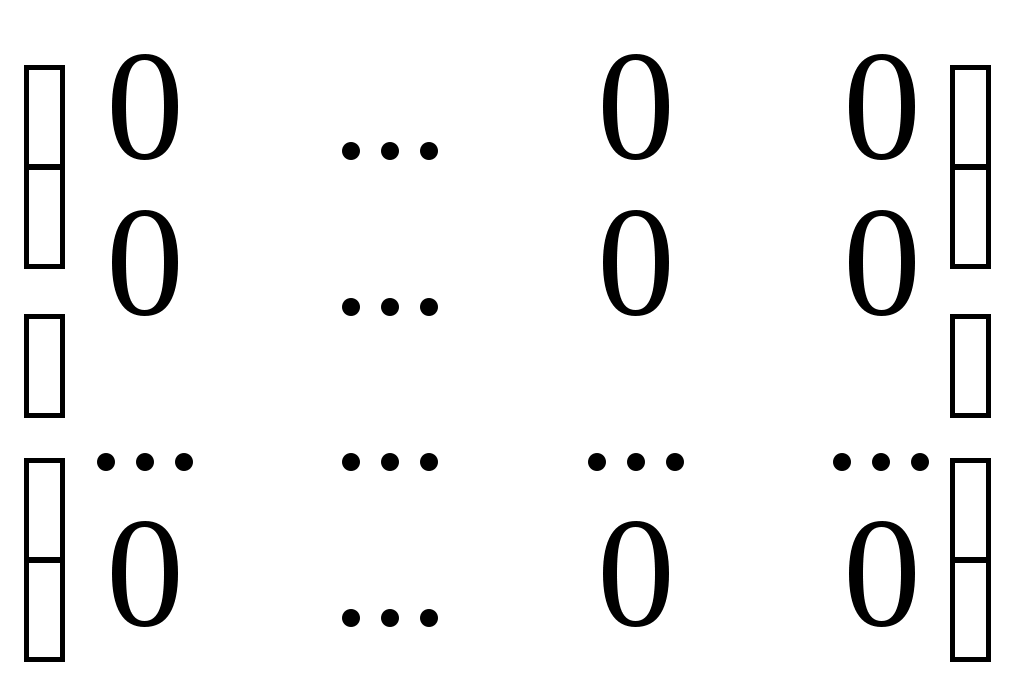 такая, что"A Î Mnn(R) 0 + А = А + 0 = А
такая, что"A Î Mnn(R) 0 + А = А + 0 = А5. "A Î Mnn(R) (-A) =
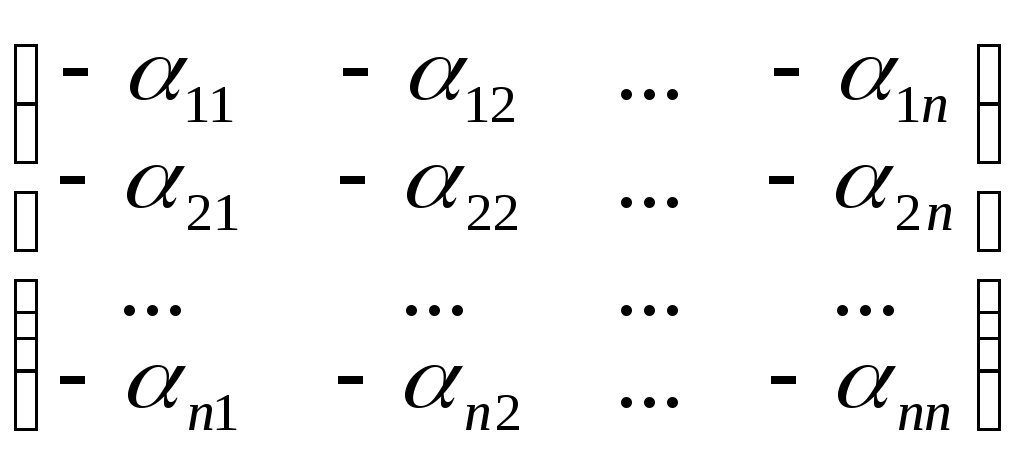 такая, что А + (-А) = (-А) + А = 0
такая, что А + (-А) = (-А) + А = 0Итак.
Определение 3. Единичной матрицей называется квадратная матрица вида:
E =
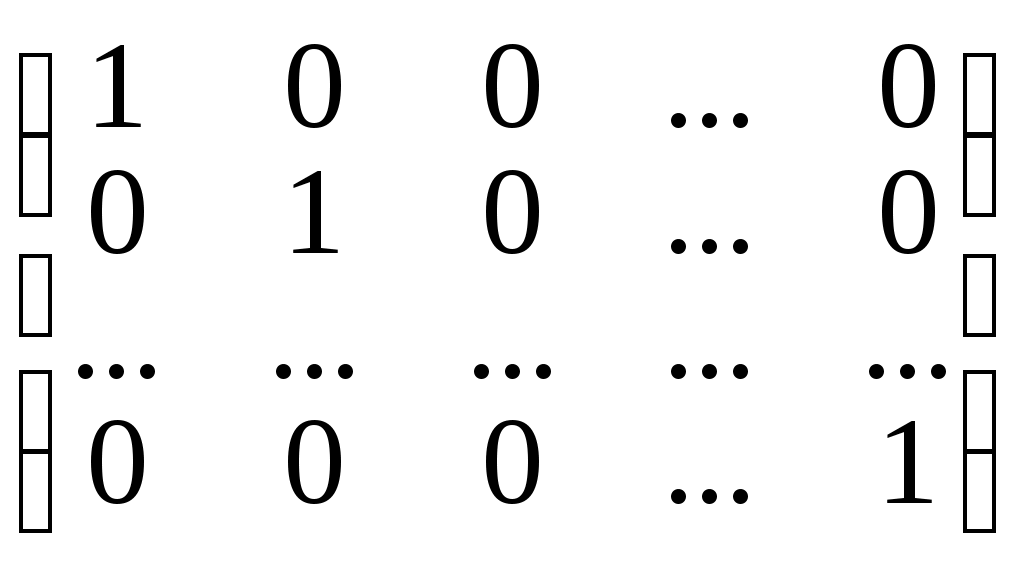 , у которой на главной диагонали стоят единицы, а все другие элементы равны нулю.
, у которой на главной диагонали стоят единицы, а все другие элементы равны нулю.Проверьте самостоятельно, что если матрицы А и Е одного порядка, то А•Е=Е•А=А, т.е., что Е играет на множестве Mnn(R) роль нейтрального элемента по умножению.
Теорема 2. Алгебра
Для доказательства нужно проверить выполнимость всех условий в определении кольца:
1. Множество Mnn(R) замкнуто относительно операций, т.к.
"A, B Î Mnn(R), (A+B) Î Mnn(R) и (A•B) Î Mnn(R)
2.
3. "A,B,CÎMnn(R), А•(В+С)=А•В+А•С, (В+С)•А= В•А+С•А.
4. "A, B, C Î Mnn(R), (A•B)•C = A•(B•C).
5. A, BMnn(R), A•B B•A.
6. E Mnn(R): A, (E•A = A•E =A).
Каждую аксиому проверьте самостоятельно.
Покажем, что в кольце Mnn(R) есть делители нуля, например, если
А =
Понятно, что таких матриц одного и того же порядка существует множество.
Запишите самостоятельно такие матрицы третьего порядка.
Теорема 3. Алгебра
Схема доказательства:
1-4)
5) "A, B Î Mnn(R) R: (A+B) = A+B.
6) , R AMnn(R) : ( + )A = A + A.
7) , R AMnn(R): ()•A = (A).
8) 1 • A = A.
Роль единичного базиса играет система матриц вида:
E1 =
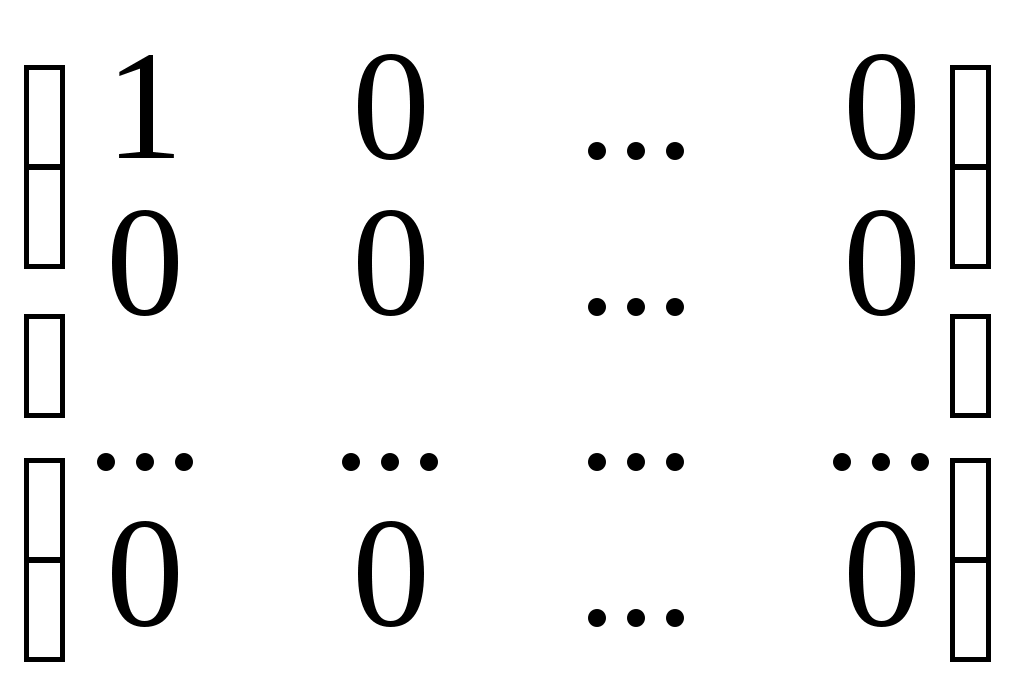 , E2 =
, E2 = 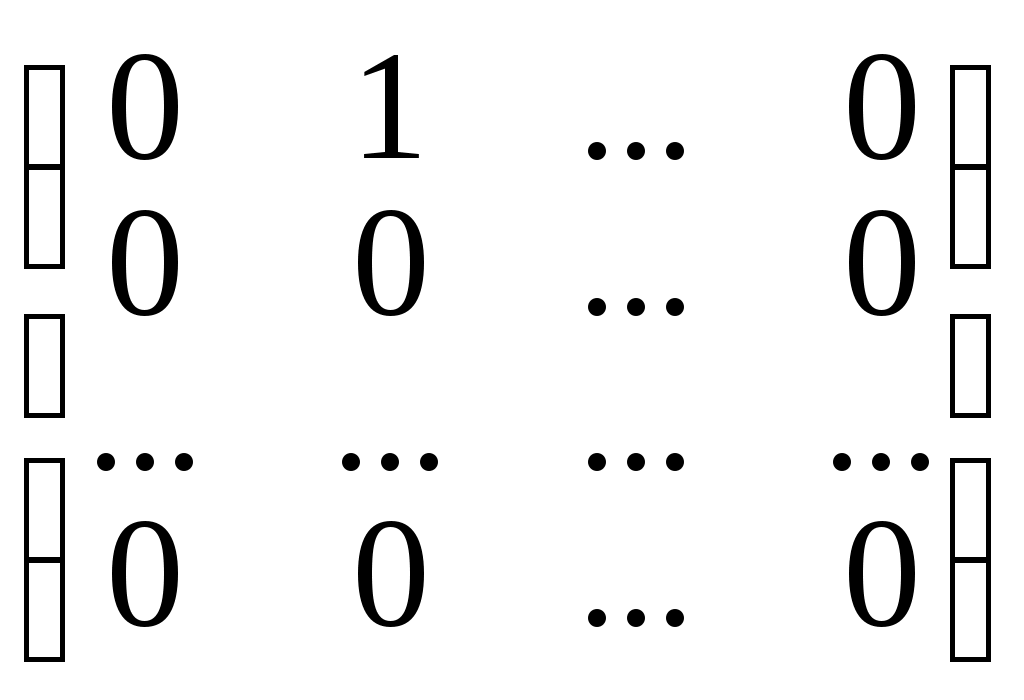 , En =
, En = 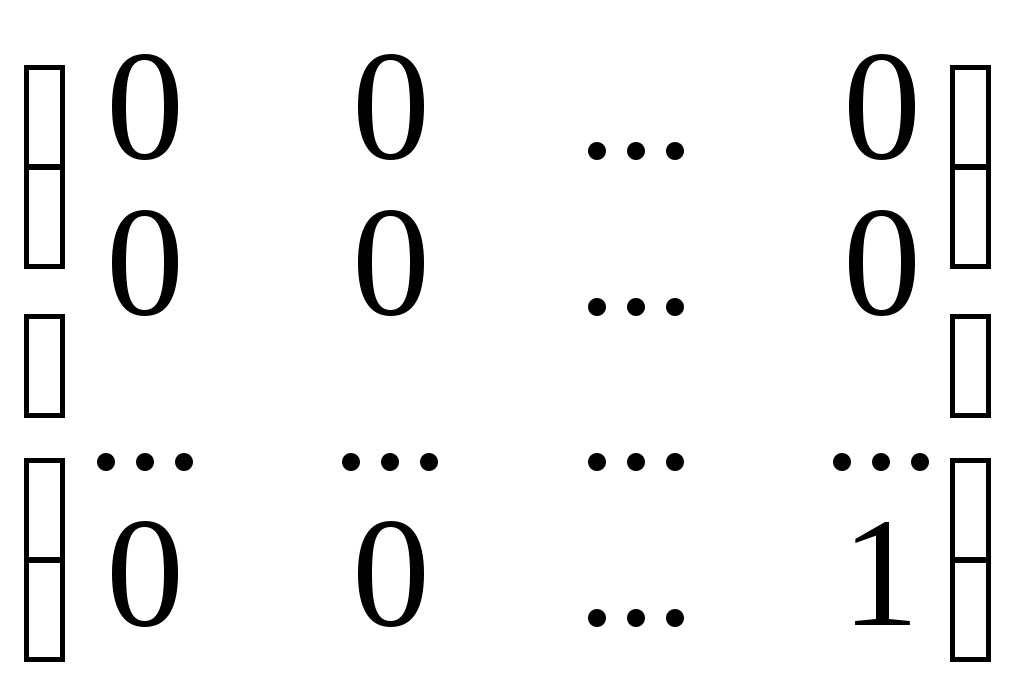
Например. В пространстве R22(R) матрица А =
Определение 4. Ведущим (главным) элементом i-ой строки матрицы А называется первый отличный от нуля элемент этой строки.
Пример 2. А=
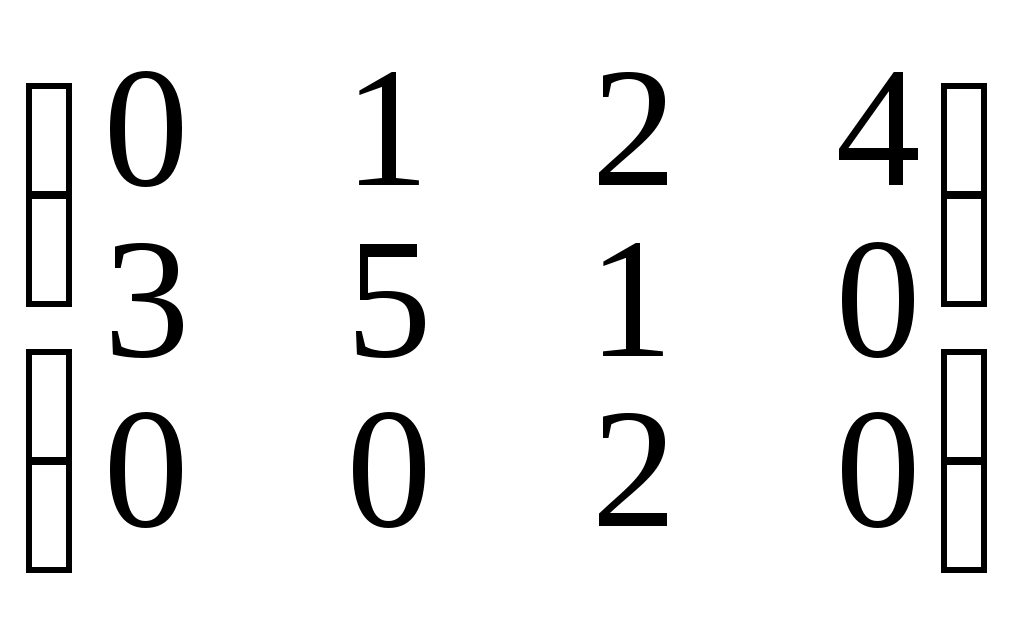 1 - ведущий элемент 1-ой строки, 3 - ведущий элемент 2-ой строки, 2 - ведущий элемент 3-ей строки.
1 - ведущий элемент 1-ой строки, 3 - ведущий элемент 2-ой строки, 2 - ведущий элемент 3-ей строки.Определение 5. Матрица А называется ступенчатой, если:
1. под ведущими элементами каждой её строки стоят нулевые элементы.
2. нулевые строчки стоят последними.
Пример 3. А =
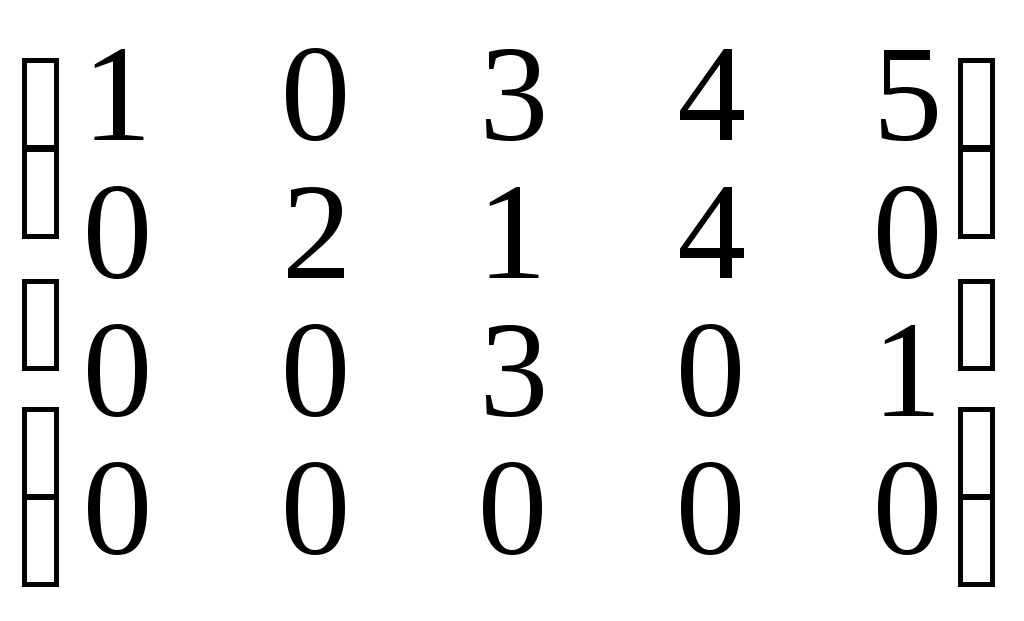 - ступенчатая матрица.
- ступенчатая матрица.Определение 6. Элементарными преобразованиями матрицы называют следующие преобразования:
1. Перемена местами строк матрицы;
2. Умножение строки на число, отличное от нуля;
3. Прибавление к одной строке другой, умноженной на число, не равное нулю.
Если на множестве матриц Mnn(R), задать отношение так: А В (когда от А к В можно перейти с помощью элементарных преобразований), то это отношение будет отношением эквивалентности.
Действительно:
1. А Mnn(R), А А (очевидно).
2. "A, B Î Mnn(R), А B => B А (достаточно совершить преобразование в обратном порядке).
3. "A, B, C Î Mnn(R), (А В) & (В С) =>(А С).
Если матрицы А и В эквивалентны, то будем записывать это так: А В.
Частным случаем этого отношения будет отношение А j В (А=В)
Определение 7. Если A = ||ik || и B = ||ik || i, k = 1...n, то А = В (ik = ik)
Теорема 4. Любую ненулевую матрицу A Mnn(R) можно привести к ступенчатому виду. Доказательство проведите самостоятельно методом математической индукции по числу строк матрицы.
Пример 4. В =
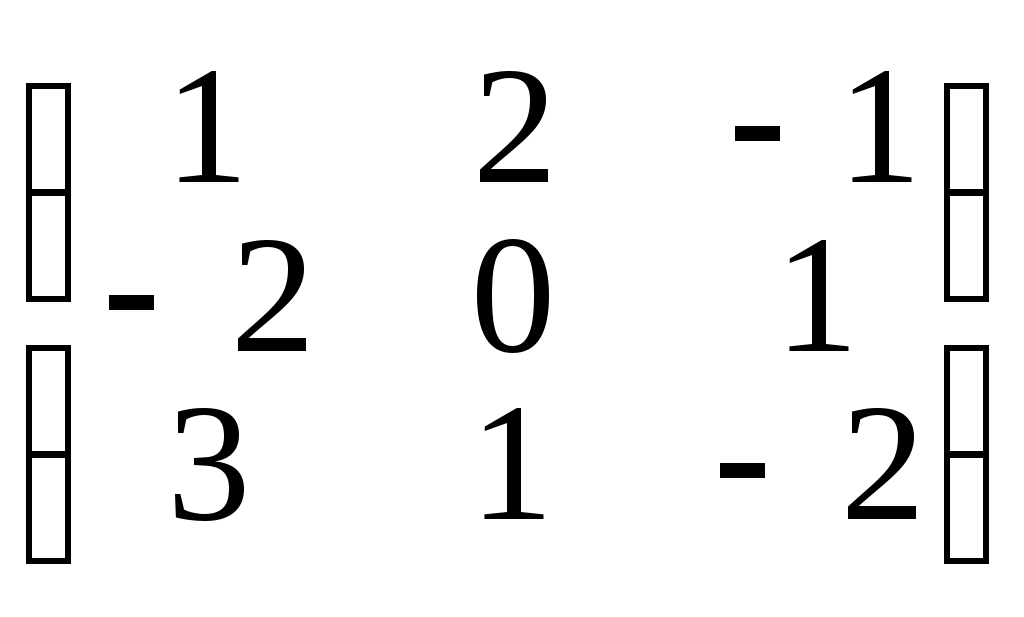
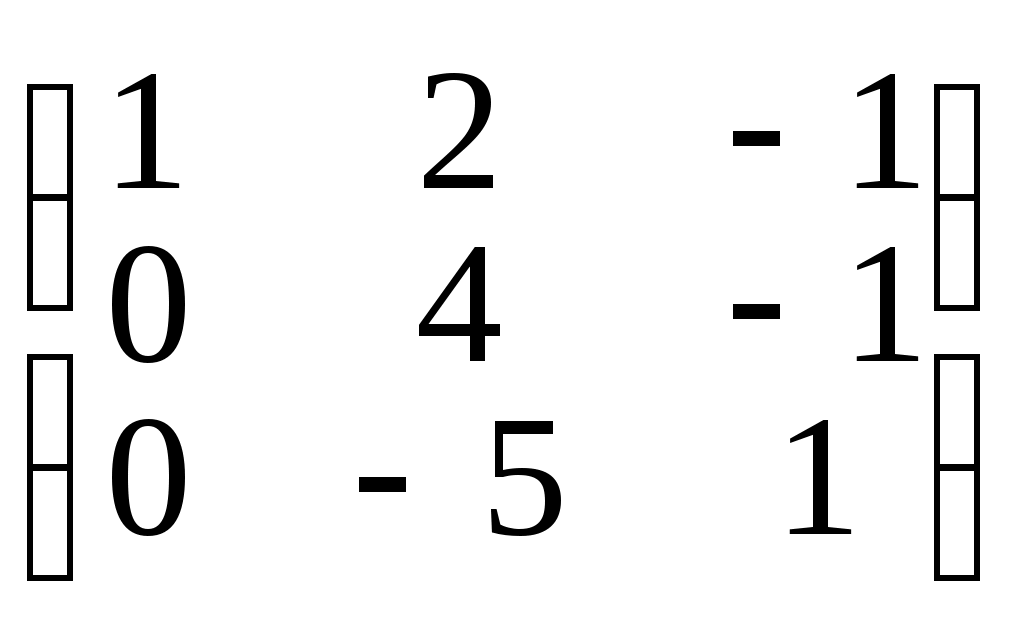 Û
Û 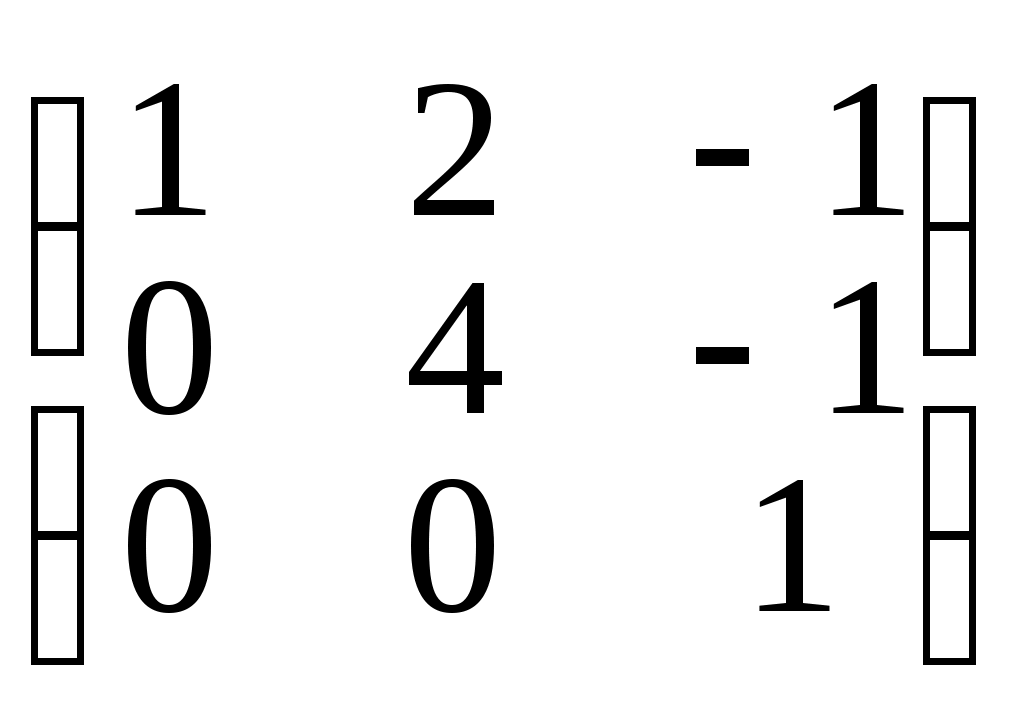
Первую строку матрицы умножили на 2 и сложили со второй строкой, затем снова первую строчку умножили на 3 и вычли из третьей строки, затем 2-ю строчку умножили на 5, 3-ю на 4 и сложили.
Определение 8. Строчным рангом ступенчатой матрицы называется число ее ненулевых строк. Обозначение: rang A = k. В примере 4 rang В = 3.
Определение 9. Матрица A = ||aik ||, где i, к = 1,2, ..., n называется обратимой (невырожденной), если существует X Î Mnn(R): А•Х = Х•А = Е.
Докажем, что такая матрица (X) единственная для А.
Предположим противное, пусть существуют матрицы X и У, удовлетворяющие определению. Тогда (Х•А)•У=Х•(А•У) в силу ассоциативности операции умножения матриц.
Тогда: Е•У=Х•Е => (У=Х).
Матрицу X называют обратной матрицей к матрице А и обозначают А-1.
Теорема 5. Если квадратная матрица А порядка nn обратима, то строчный ранг её ступенчатой матрицы равен n.
Доказательство: Так как матрица А обратима, то А-1: А • А-1= Е (rang E=n) => (rang A=n). (Справедлива и обратная теорема. Докажите её самостоятельно).
Теорема 6. Любую обратимую матрицу A Î Mnn(R) с помощью элементарных преобразований можно привести к единичной матрице Е (т.е. матрица А эквивалентна единичной матрице Е).
Эта теорема является следствием теоремы 4.
Поэтому алгоритм нахождения обратной матрицы основан на том, что матрицы (А/Е) и (Е/А-1) - эквивалентны, и состоит в следующем:
1. К квадратной матрице А справа приписывается единичная матрица того же порядка, что и А, (А/Е);
2. С помощью элементарных преобразований от матрицы (А/Е) переходят к матрице (Е/А-1);
3. Записывают А-1 отдельно.
Замечание 1. В процессе нахождения обратной матрицы не обязательно проверять - обратима ли матрица, т.к. при элементарных преобразованиях сразу будет видно, имеет ли она обратную матрицу.
Пример 5. Найти обратную матрицу для матрицы
A =
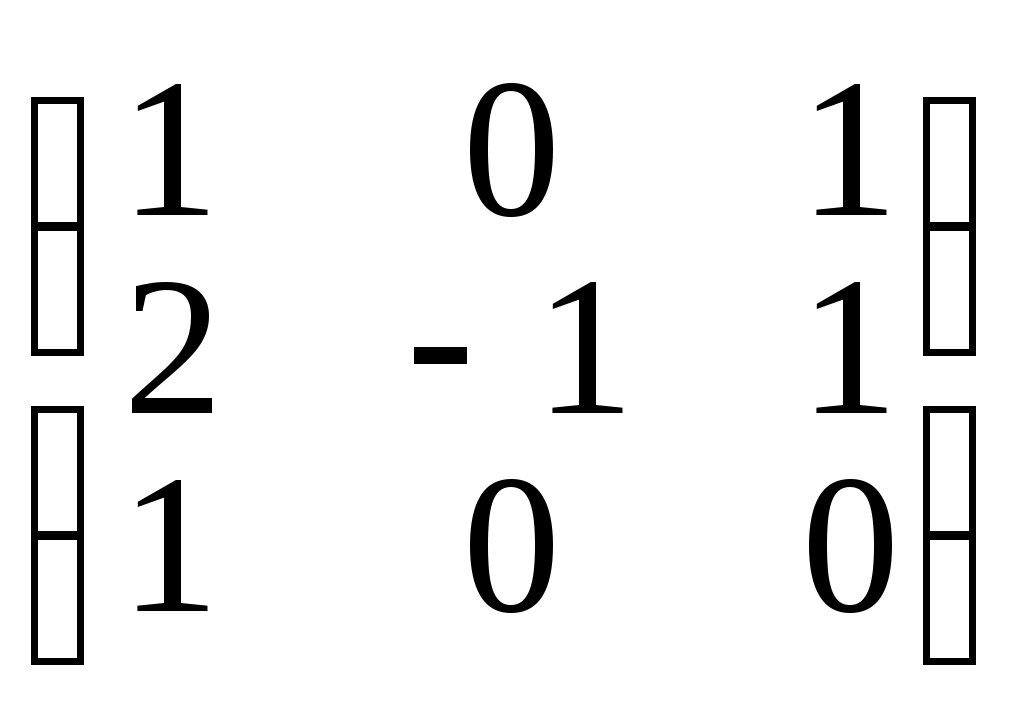 rang A=3 (проверьте), значит она обратима.
rang A=3 (проверьте), значит она обратима. Найдем А-1
(А/Е) =
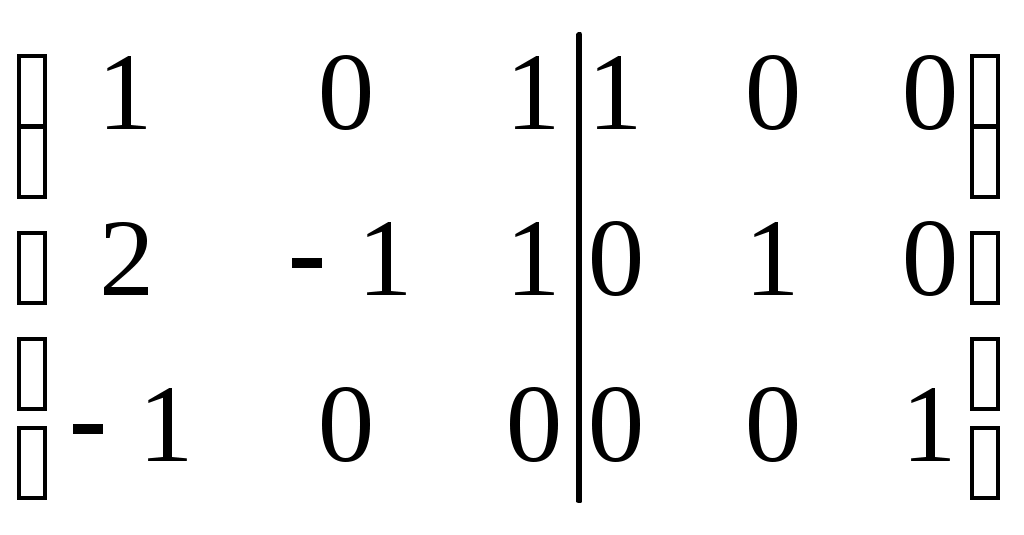
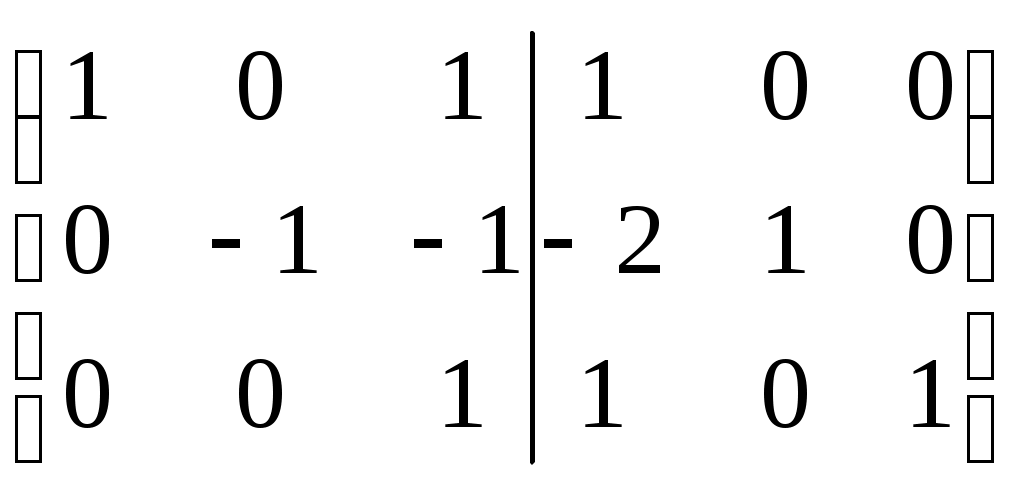 Û
Û 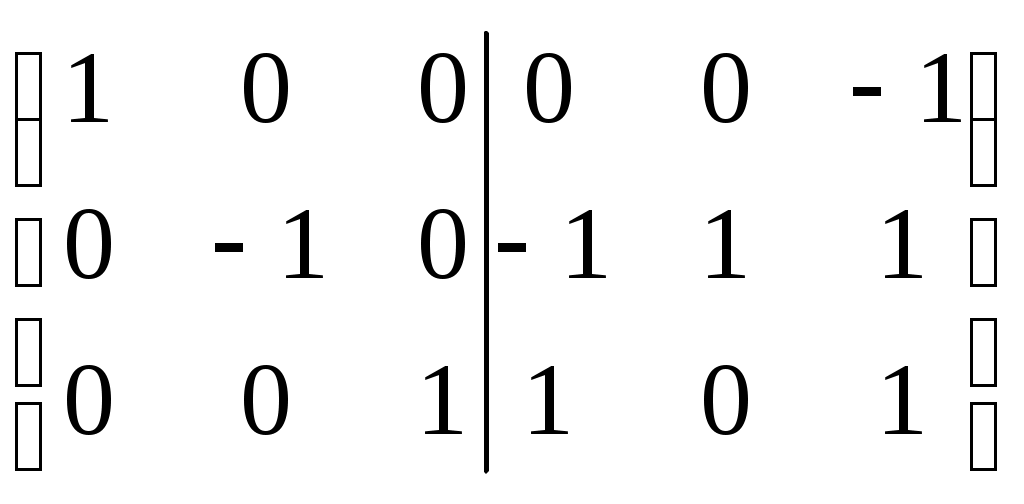 Û
Û 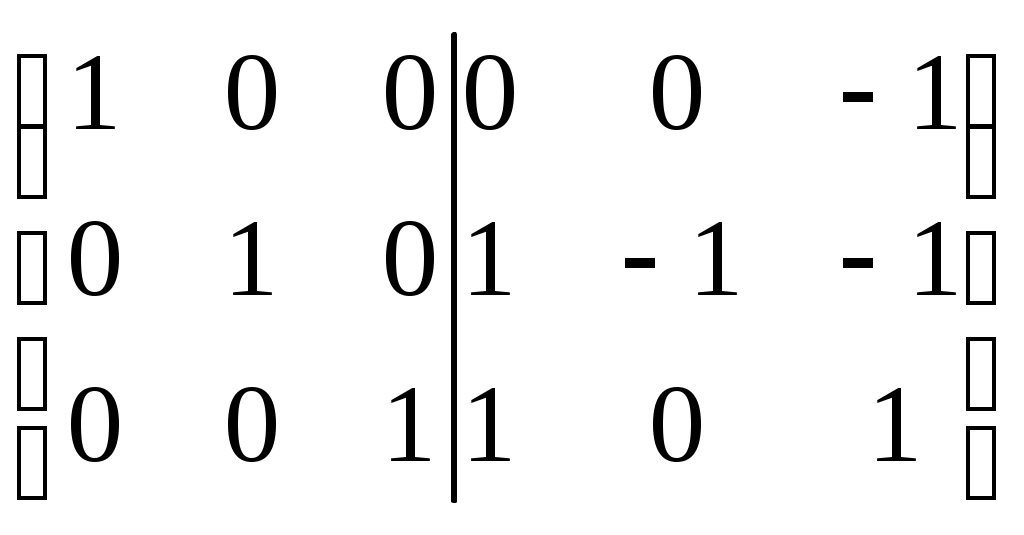 => A-1 =
=> A-1 = 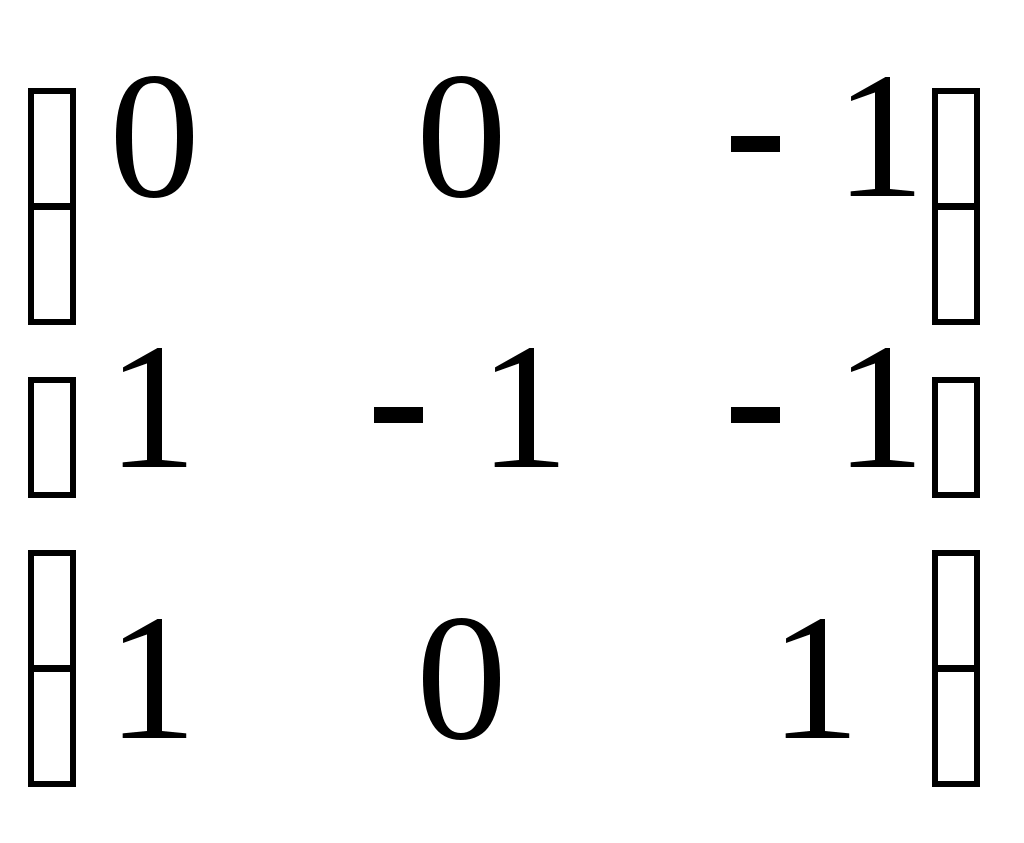
Проверка: А • A-1 =
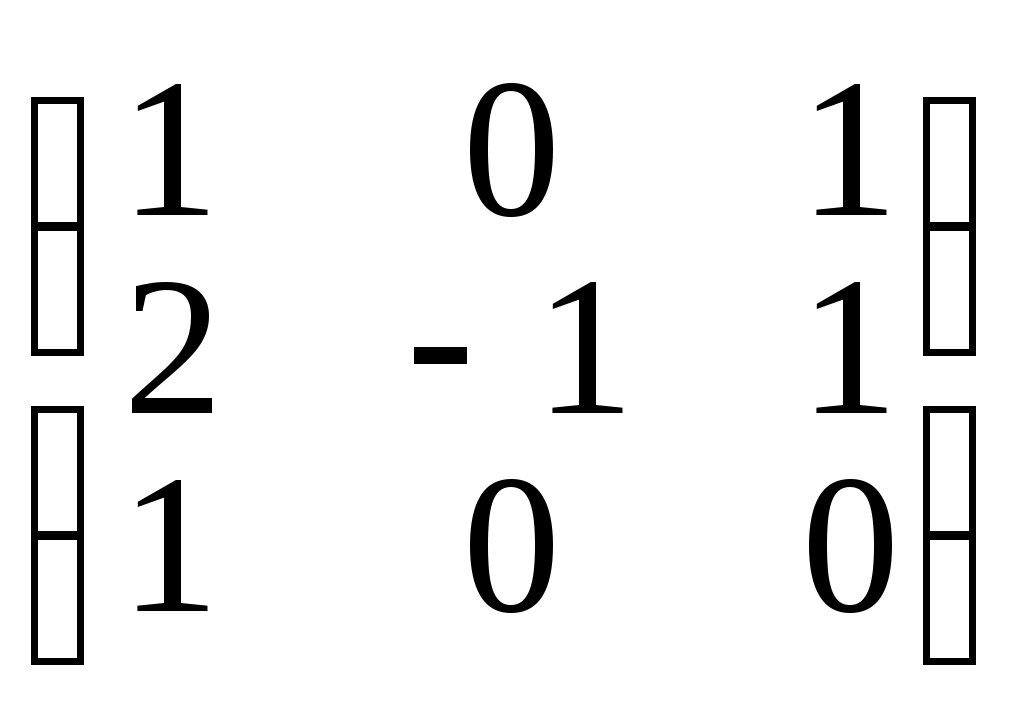
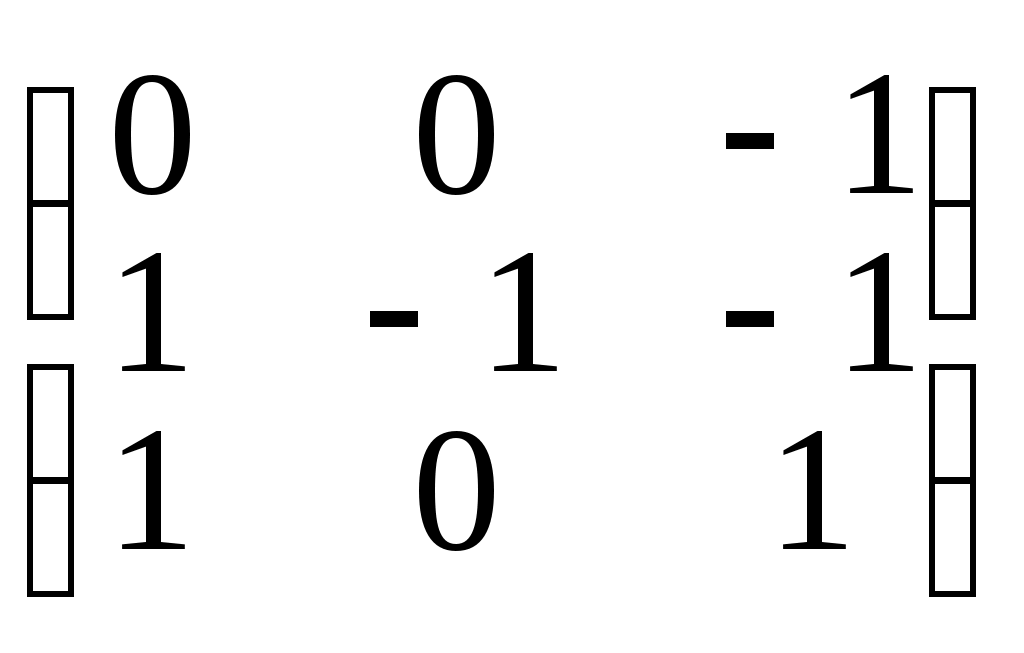 =
= 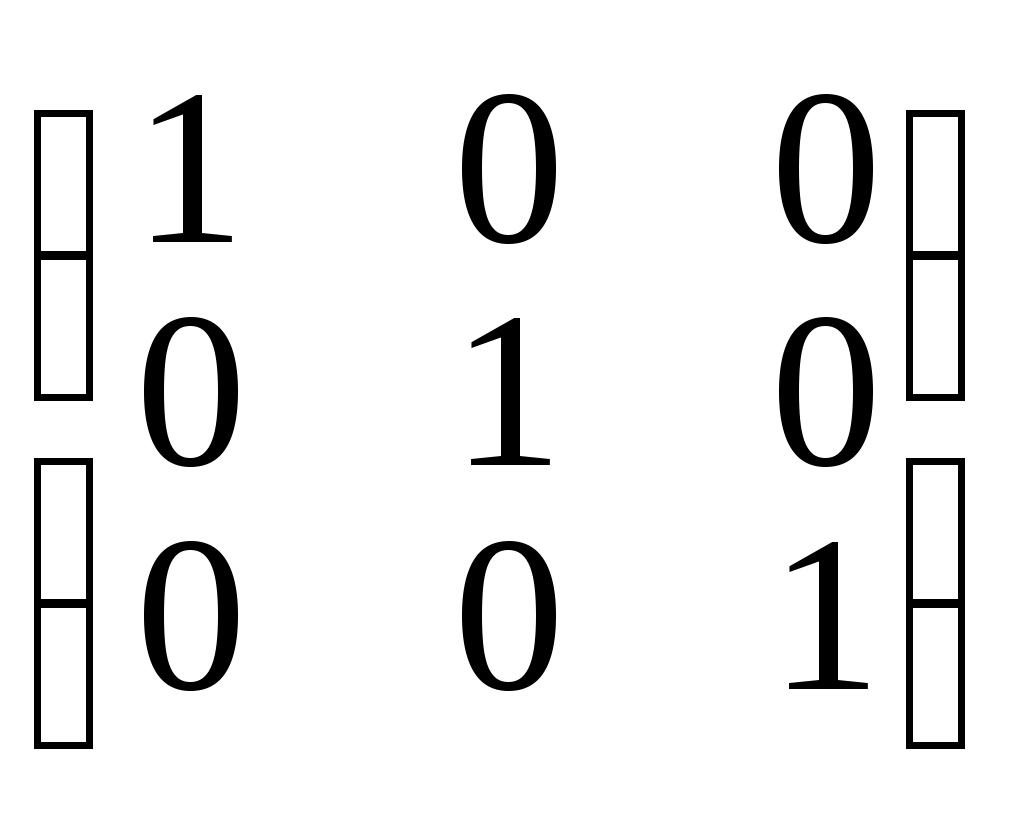
С помощью обратной матрицы можно решать матричные уравнения, в которых роль переменной играет матрица X
Пример 6. Решить в общем виде уравнение. X • A + X = B
Решение.
Чтобы матрицу X можно было вынести за скобки, нужно представить слагаемое X =Е•Х, тогда Х•(А+Е) = В. Нельзя писать, что Х•(А+1) = В, т.к. А+1 не имеет смысла во множестве Rmn(R). Если матрица (А+Е) будет невырожденной, т.е. имеет обратную матрицу (А+Е)-1, то получим уравнение X (А+Е) (А+Е)-1 = В (А+Е)-1 , т.к. умножение матриц некоммутативно, то в этом случае нужно умножать справа, тогда X • Е = В•(А+Е)-1 или Х = В•(А+Е)-1
Если матрица (А+Е) не имеет обратной матрицы, то исходное уравнение таким способом решать нельзя.
Пример 7. Решить матричное уравнение:
Решение.
1. Представим уравнение в виде А•Х•В = С
2. Выразим матрицу X: Х = А-1•С•В-1
3. Найдем А-1 и В-1:
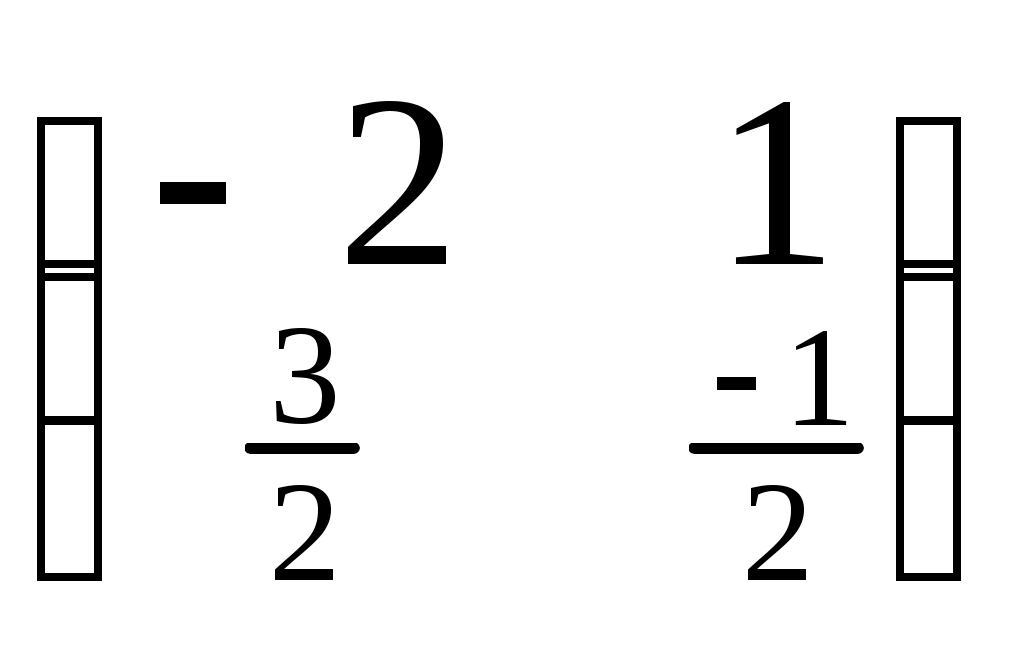
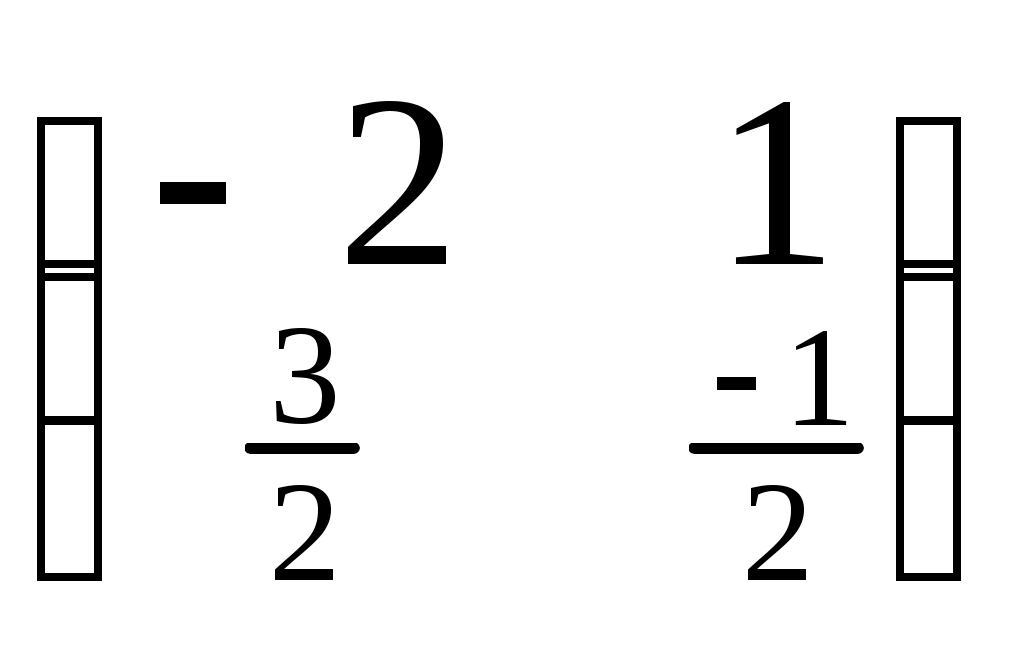 •
•