Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc

§2. Определители, их свойства.

Пусть дано конечное множество М; в качестве такого множества можно взять М = {1,2,..,n}.

Определение 1. Биекция : М  М называется подстановкой n-ой степени.

Обозначим множество всех подстановок на множестве М через .

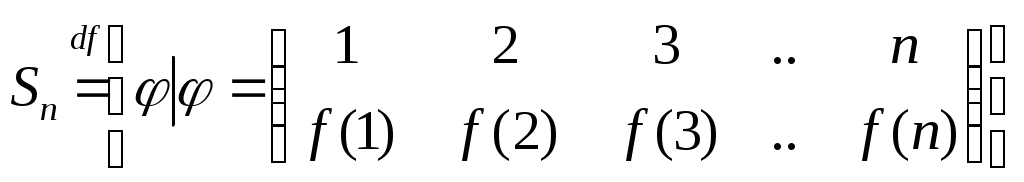Докажите самостоятельно, что |S_n| = n!

Определим на множестве S_n операцию композиции двух подстановок (биекций) xM x(  )=(x).

Замечание 1. Из определения следует, что композиция двух подстановок будет снова подставной, т.е. множество S_n замкнуто относительно операции композиции (по теореме о композиции биекций).

Пример 1. Найти композицию двух подстановок:

, видим, что        , т.е. операция (°) некоммутативна.

Пусть дано множество М={ l,2,..,i ,k,...n}.

Запишем одну из перестановок этого множества, например, (1,2,...i, k…n)

Будем говорить, что пара элементов (i, к) образует инверсию, если:

1. i > k.

2. i стоит впереди (слева) от к.

Определение 2. Перестановка называется четной, если в ней четное число инверсий и нечетной, если в ней нечетное число инверсий.

Пример 2. Пусть М = {1,2,3,4,5}, (3,1,4,2,5) одна из его перестановок.

Определим число инверсий в этой перестановке. Для этого поступаем так:

Находим наименьший элемент (это 1), зачеркиваем его и считаем, сколько элементов стоит впереди 1, которые больше 1. Видим, что это одно число 3, затем зачеркиваем двойку и считаем, со сколькими элементами она находится в инверсии и так продолжаем до последнего числа:

1+2+0+0+0=3. Следовательно, перестановка (3.1,4,2,5) - нечетная.

Определение 3. Подстановка j = называется четной, если перестановка, стоящая в ее нижней строке, будет четной.

Пример 3. j = - нечетная (проверьте!)

Определение 4. Sg n j =

---

Запись: Sgn j =1 читается так: "знак подстановки j равен 1".

Из определения следует, что Sgn  = 1, действительно, подстановка  = - четная.

Sg n j^-1 = Sg n j, j^-1 =
Определение 5.

Подстановка  = называется транспозицией элементов (i, k).

Теорема 1. Sg n = -1 Докажите самостоятельно.

Теорема 2. Алгебра o> конечная группа.

Проверьте самостоятельно аксиомы:

1.  , ,   Sn (  )   =   (  )

2.    Sn:    Sn (   =  = )

3.    Sn  ^-1  Sn:   ^-1 = ^-1   = 

4. |Sn| = n!

Эту некоммутативную группу называют симметрической группой подстановок степени (n) и обозначают _n=

Обозначим через An - множество всех четных подстановок группы _n

Теорема 3. <Аn, > - подгруппа группы _n, ее называют знакопеременной группой подстановок n-ой степени.

Докажите самостоятельно.

Определение 6. Определителем (детерминантом) n-го порядка квадратной матрицы А = ||_ik||, i, к=1, 2, 3, ...,n называют сумму вида:

Sgn  _1(1)  _2(2)  …_n(n) , где Sn =

Sgn j =

Обозначается эта сумма короче символами det A или |А|. Если это определение проговорить словами, то получится следующее:

«Определителем n-го порядка квадратной матрицы А называют алгебраическую сумму всевозможных членов, каждый из которых представляет собой произведение n-элементов, взятых по одному и только одному разу из каждой строки и каждого столбца матрицы А, знак любого члена определяется четностью (нечетностью) подстановки его индексов».

Непосредственно из определения определителя n-го порядка следует истинность следующих утверждений:

1. Определитель n-го порядка имеет n! членов.

Действительно, суммирование введется по всем подстановкам Sn, а множество Sn имеет ровно n! членов, так как на множестве М = {1, 2,...,n} из n элементов можно задать n! подстановок (каждая подстановка является биекцией  : М М).

2. Половина членов определителя будет иметь знак (+), половина - (-), так как половина подстановок будут четными, половина - нечетными.

3. Определитель, в котором какая-то строка или столбец нулевые, будет равен нулю.

Действительно, в этом случае каждый член определителя

_1(1) _2(2) …_n(n) в качестве одного из сомножителей будет содержать ноль.

4. Если все элементы какой-либо строки (столбца) определителя n-го порядка имеют общий множитель, то его можно вынести за знак определителя (суммы).

Действительно, тогда Используя определение детерминанта n-го порядка, найдем разложение определителя 3-го порядка.



Матрица А= 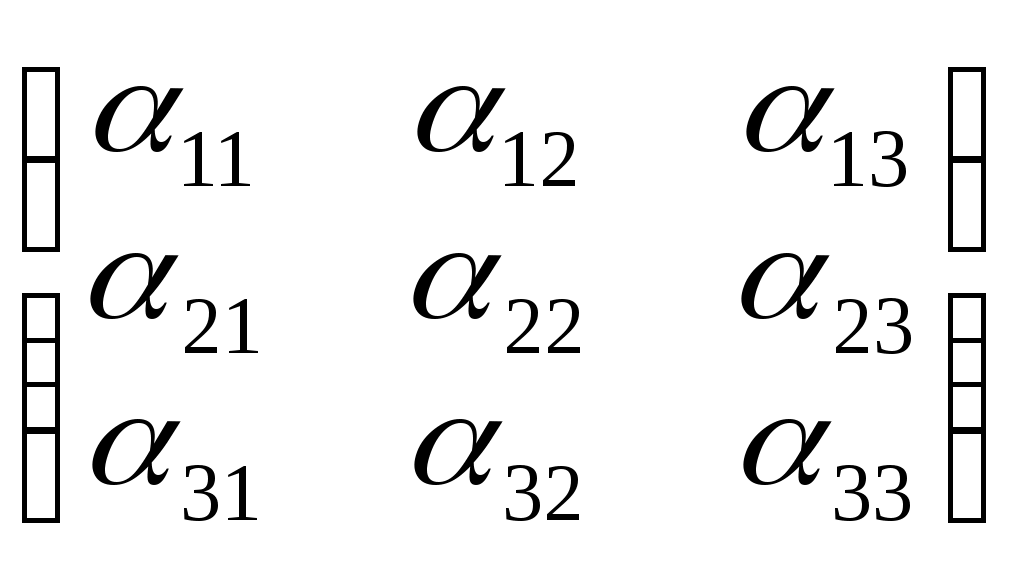S₃ =

Найдем все подстановки из множества S₃ и определим их четность.

- четная; - нечетная;

- нечетная; - четная;

- нечетная; - четная;

Теперь запишем разложение определителя 3-го порядка:

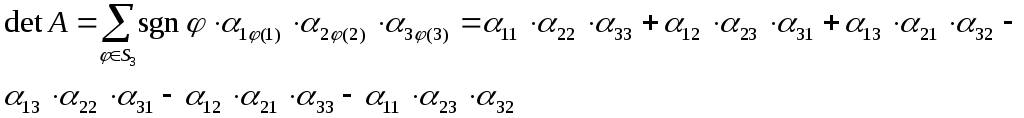Из этого разложения видно, что члены со знаком "+" и со знаком "-" выбираются по схемам, которые носят название "'Правило Саррюса".



Пример 4: Вычислить определитель:

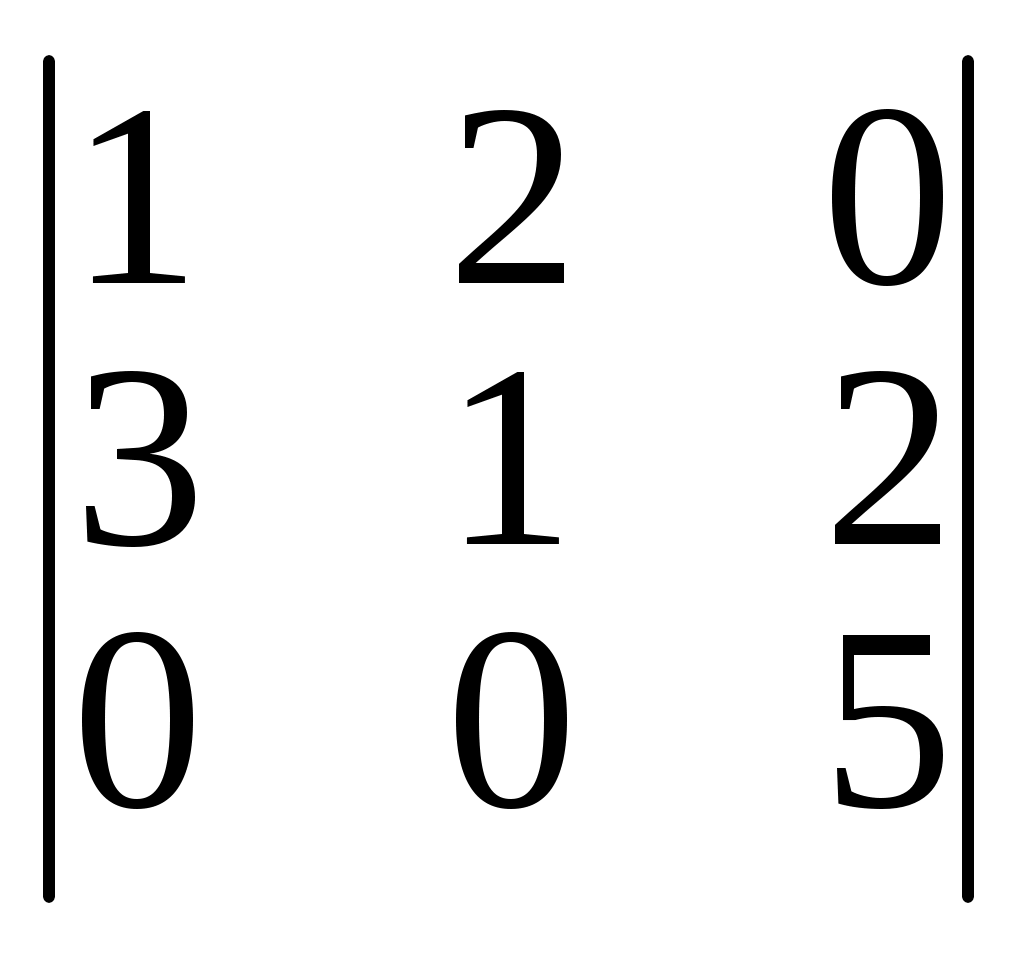=1•1•5 +2•2•0 + 3•0•0 - 0•1•0 -3•2•5 -0•2•1=5 -30= -25

Опираясь на определение детерминанта, можно записать его разложение для порядка n = 4, n = 5, ... Но при этом число членов определителя будет стремительно возрастать.

При n = 4 определитель будет иметь 4! = 1•2•3•4 = 24 члена, при n = 5 уже 5! = 1•2•3•4•5 = 120 членов, при n = 6,

6! = 1•2•3•4•5•6 = 120 • 6 = 720 членов и т.д. Поэтому определители порядка выше n = 3 вычисляют, опираясь не на его определение, а на его свойства.

Основную роль при этом играет такое свойство: элементарные преобразования над строчками (столбцами) определителя n-го порядка не изменяют его значения. Поэтому определитель любого порядка с элементами из поля R может быть приведен к так называемому «треугольному» виду:

Например:

а) det A = =

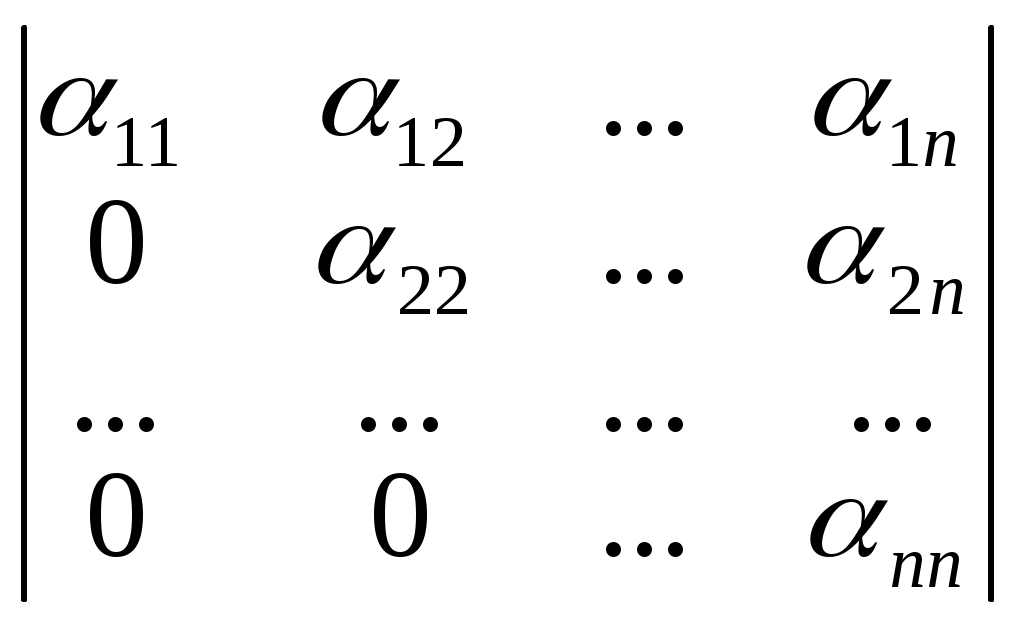б) det A= =

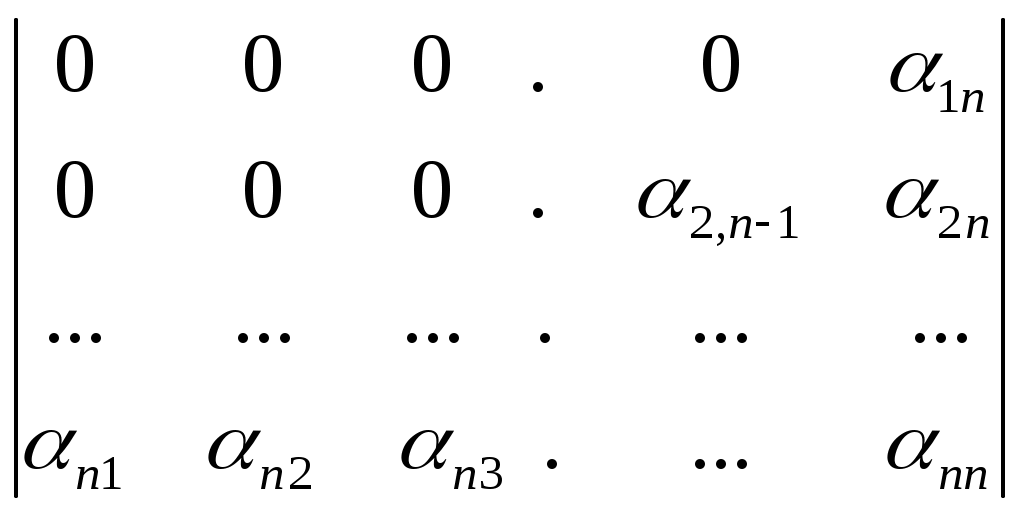в) = = = =

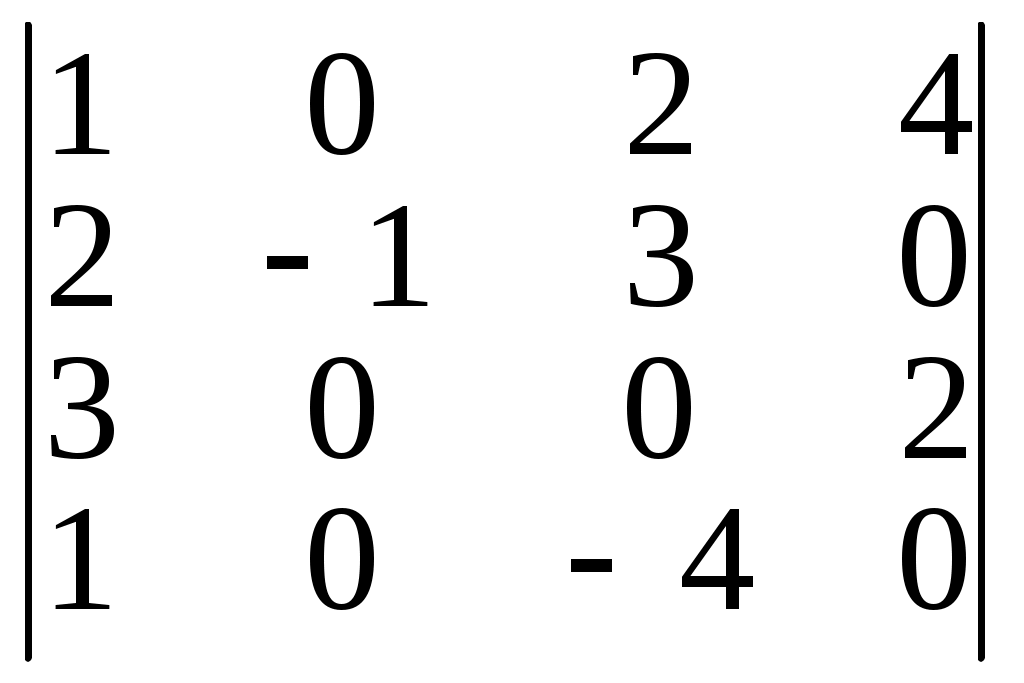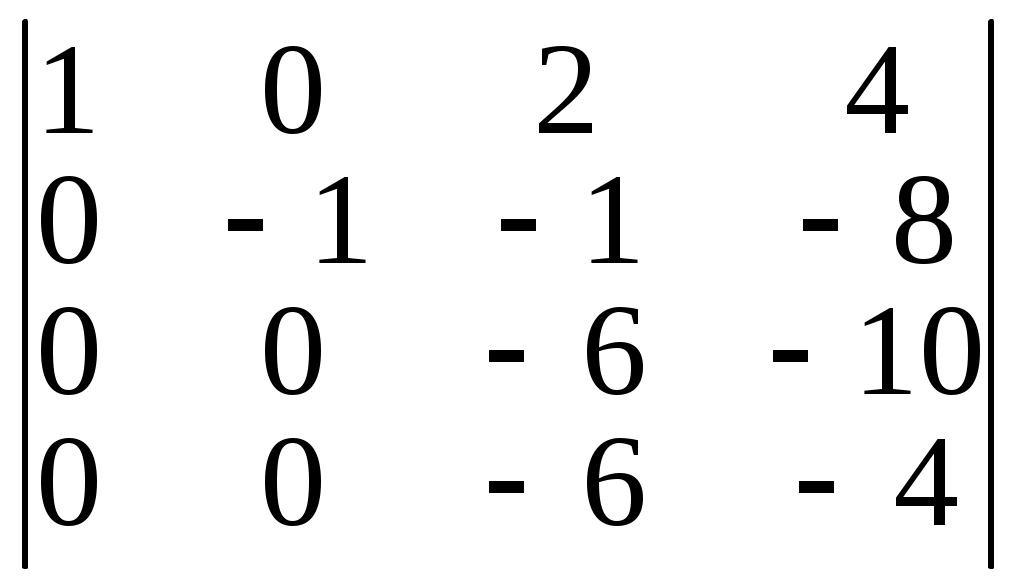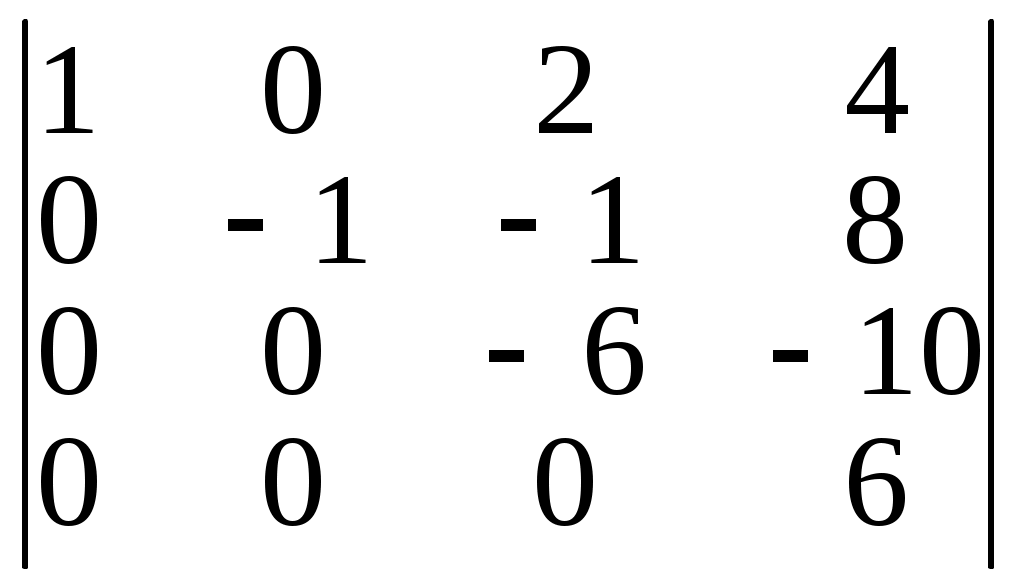Понятия минора и алгебраического дополнения элемента _ik определителя n-го порядка позволяют вычислять определители путем разложения их по строке или столбцу, а так же понижать порядок определителя.

Определение 7. Минором M_ik элемента определителя
n-го порядка называется определитель (n-1) порядка, который получается из данного определителя путем вычеркивания i - й строки и k - гo столбца.

Определение 8. Алгебраическим дополнением A_ik элемента _ik определителя n-го порядка называют минор M_ik, взятый со знаком (-1)^i+к, т.е. А_ik = (-1)^i+к M_ik,

Пример 5. Вычислить А₂₃ элемента ₂₃ определителя |А| = =

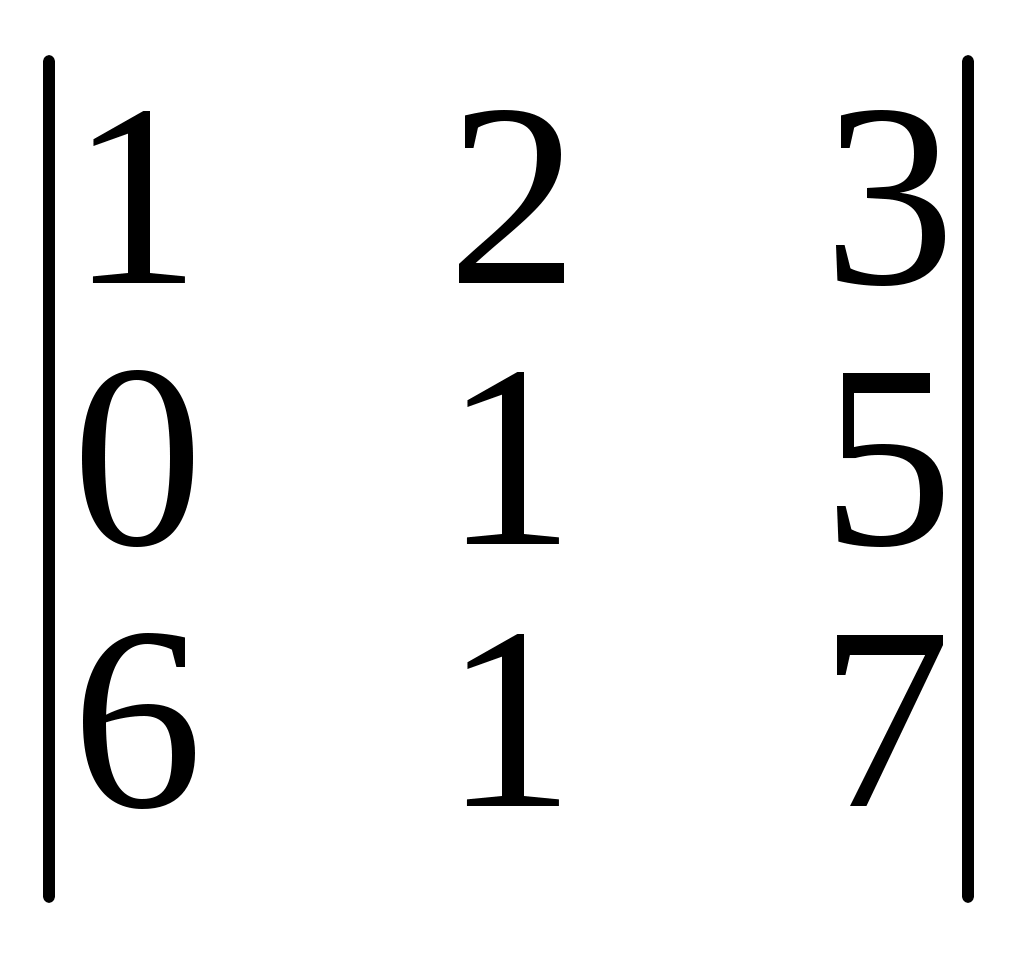
1. Находим минор M₂₃ элемента ₂₃. Дня этого вычеркиваем вторую строчкуи третий столбец, получаем определитель:

= 1 - 12 = -11

2. Итак. М₂₃ = -11. Тогда А₂₃ = (-1)²⁺³М₂₃ = -М₂₃ =11

Теорема 4. Докажите,

что det A =

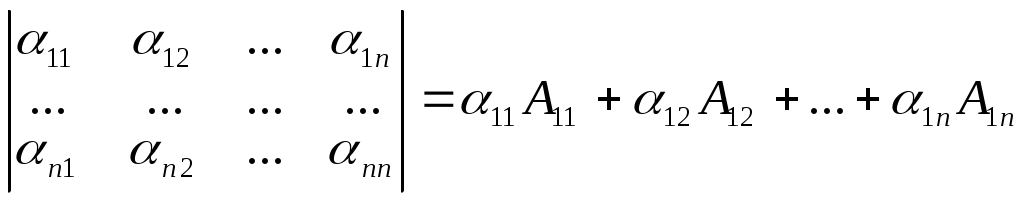
(самостоятельно).

1   2   3   4   5   6   7   8   9   ...   16

---

Глава 3. Системы линейных уравнений, методы их решения.

Основными понятиями этой темы служат понятия: система линейных уравнений, ее расширенная матрица, элементарные преобразования систем и матриц, их взаимосвязь.

Определение 1. Системой (s) линейных уравнений с (n) переменными называется система вида:

1)

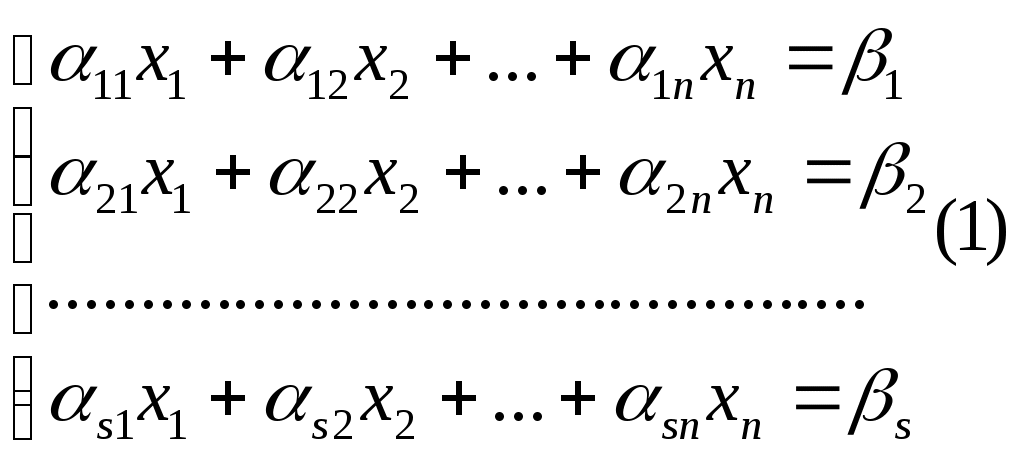
где _ik R (i=1, 2, ..., s) (k=1, 2,..., n)

2) Систему (1) можно записать короче в виде:

i = 1, 2,...,s, _ik называют коэффициентами, x₁,x₂,…,x_n- переменными, _i- свободными членами, ₁₁x₁,…, _snx_n - членами уравнений.

Определение 2. Решением системы уравнений (1) называется набор чисел (₁,₂,...,_n)таких, что при их подстановке соответственно вместо x₁, x₂,.., x_n каждое уравнение системы обращается в верное равенство.

В этом случае говорят, что набор (₁,₂,...,_n) удовлетворяет системе (1). Решить систему - это значит найти все ее решения (или доказать, что их не существует).

Определение 3. Две системы уравнений

и

называются равносильными (эквивалентными), если каждое решение одной системы является решением другой, и обратно: каждое решение второй является решением первой.

Другими словами, можно сказать, что равносильные системы имеют одно и то же множество решений.

Заметим, что эквивалентные системы могут иметь разное число уравнений. Например,



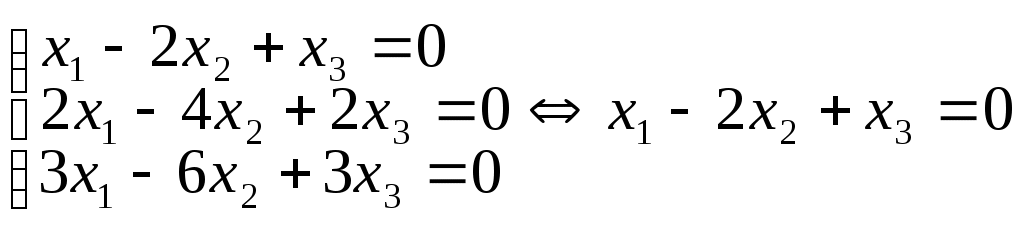
а также то, что две системы, не имеющие решений, будут считаться эквивалентными, исходя из определения 3.

Определение 4. Если система (1) имеет хотя бы одно решение, то она называется совместной, в противном случае - несовместной; если она имеет единственное решение, то она называется определенной

---

, если больше одного решения, то неопределенной.

Определение 5. Элементарными преобразованиями системы линейных уравнений называют следующие преобразования:

1. Перемена местами уравнений системы.

2. Умножение уравнений на число, не равное нулю.

3. Прибавление к одному из уравнений системы другого, умноженного на число.

4. Удаление из системы нулевого уравнения.

Докажите, что всякое элементарное преобразование системы (1) приводит к системе, равносильной данной.

Таблицу А= 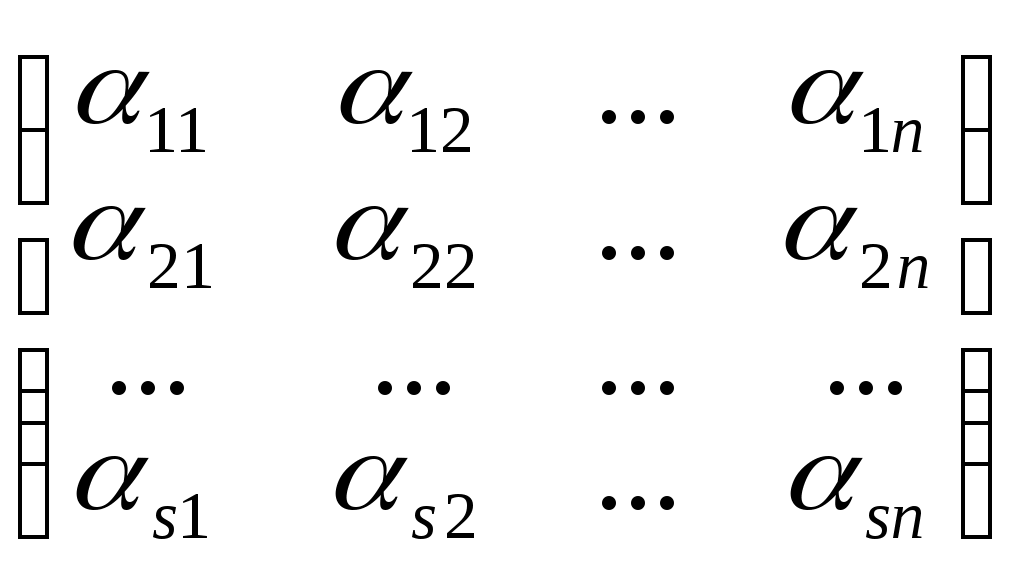называют матрицей системы 1)
Матрицу В= 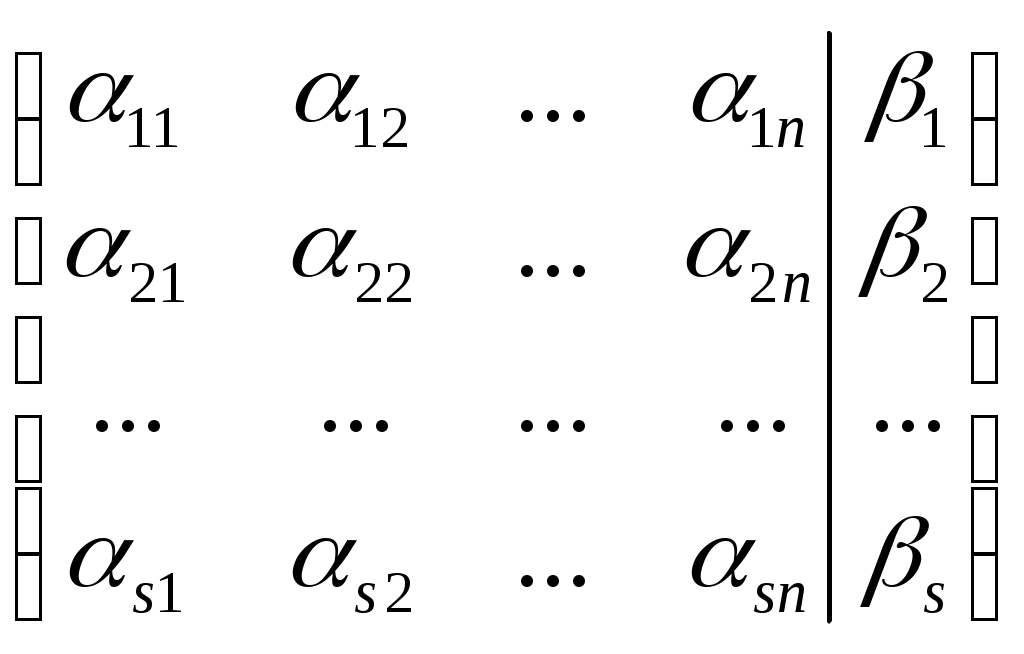называют расширенной матрицей системы 1).
Матрицу В также называют табличной записью системы 1), а запись 1)-полной записью системы. Ясно, что по табличным записям всегда можно воспроизвести полную запись.
Например, пусть

В= 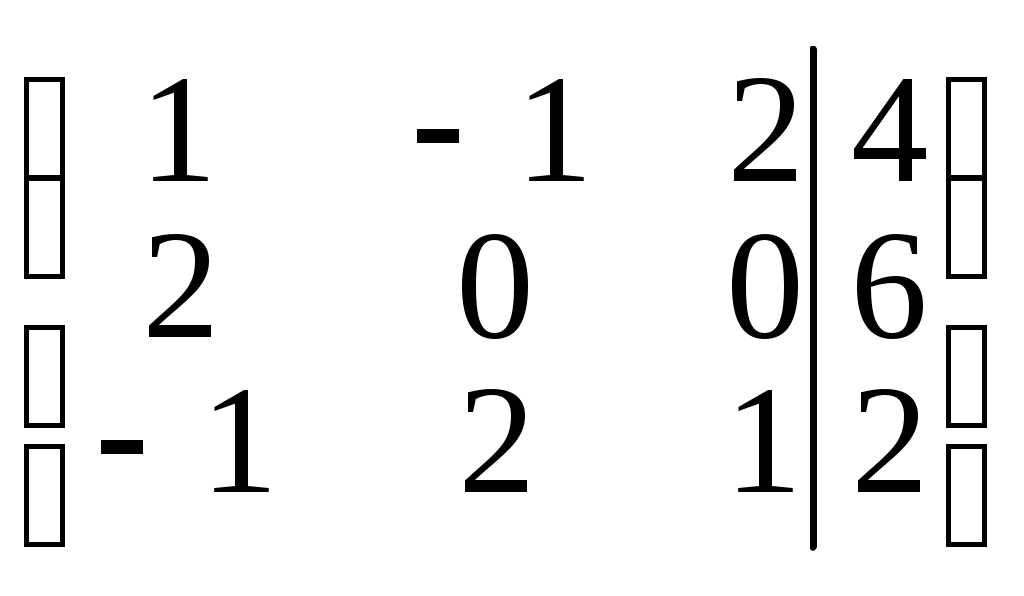, тогда система будет иметь вид: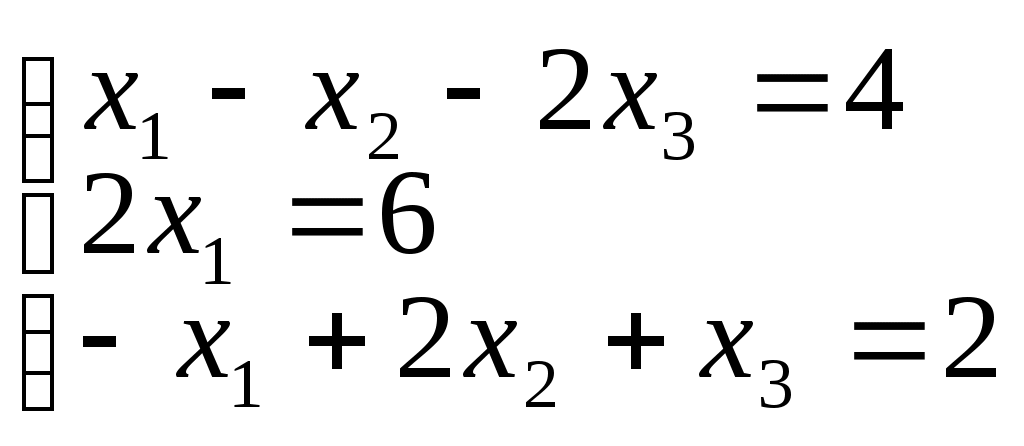

Табличная запись системы 1) более компактна, чем полная запись и более удобна для проведения элементарных преобразований системы линейных уравнений. Например, при умножении уравнения на число все коэффициенты и свободный член умножаются на это число. Следовательно, в табличной записи все элементы соответствующей строки матрицы умножаются на это число. Таким образом, элементарные преобразования системы линейных уравнений можно заменить соответствующими элементарными преобразованиями системы строк расширенной матрицы В.

Теорема 1. Пусть система (1) имеет расширенную ступенчатую матрицу В, ведущие элементы которой , тогда если последний ведущий элемент _rl удовлетворяет условиям:

1) l=n+1 -система будет несовместной,

2) (l=n)&(r=n) - система будет определённой,

3) (r
На этой теореме основан универсальный метод решения любой системы линейных уравнений, который называют методом Гаусса или методом последовательного исключения переменных.

Основные шаги алгоритма этого метода:

I. Записывается расширенная матрица В данной системы.

II. Затем матрица В с помощью элементарных преобразований приводится к ступенчатому виду.

---

III. На основании теоремы определяется решение данной системы.

Пример 1. Решить систему с помощью метода Гаусса.

а)

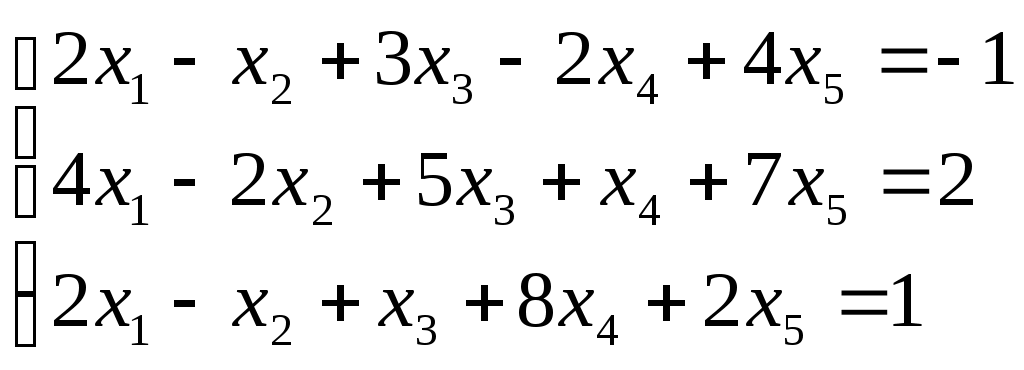
Решение. 1. Записываем матрицу B



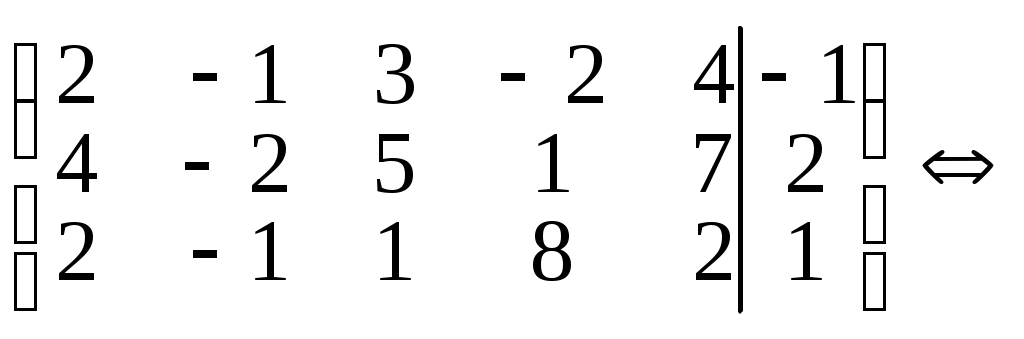
2. Приводим ее к ступенчатому виду



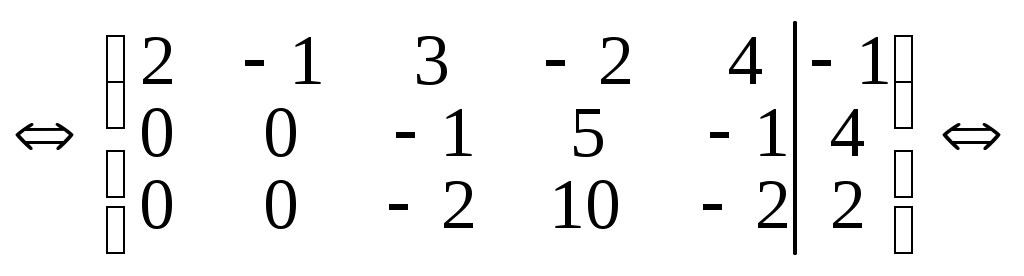
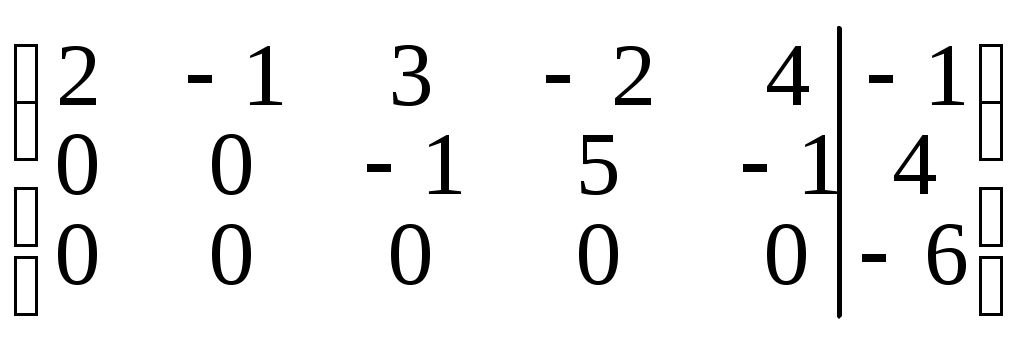
3. Записываем ступенчатую систему на основе полученной ступенчатой матрицы.



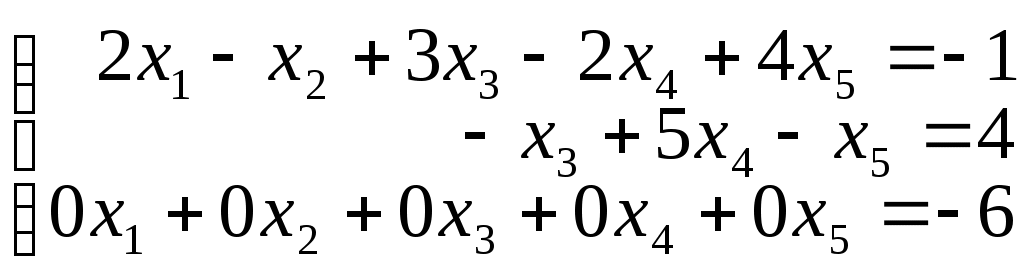
Последнее уравнение системы противоречиво, следовательно, система не имеет решений.

b)

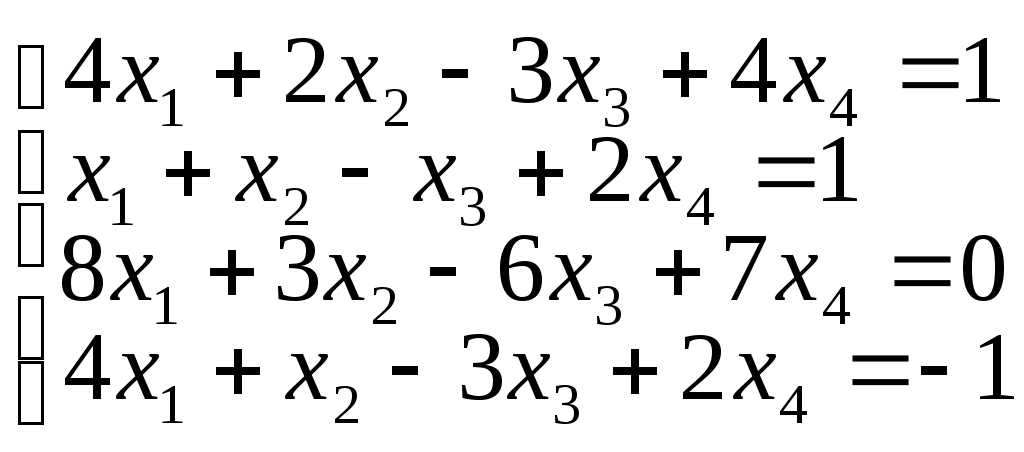
Решение.

Записываем соответствующую данной системе матрицу В и приводим её к ступенчатому виду.

B=



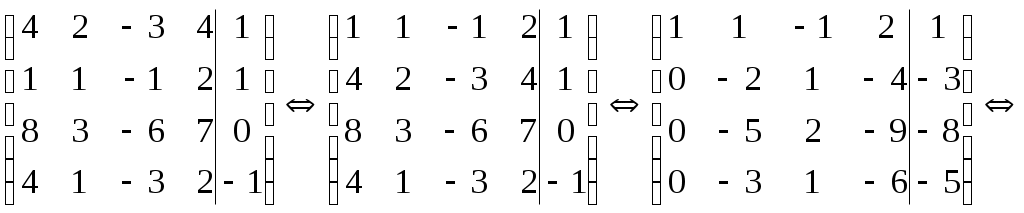
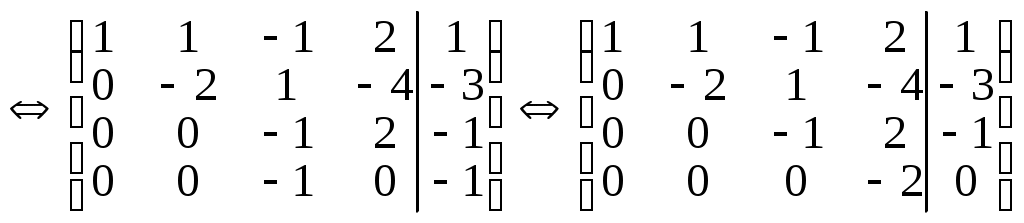
По полученной матрице запишем систему:



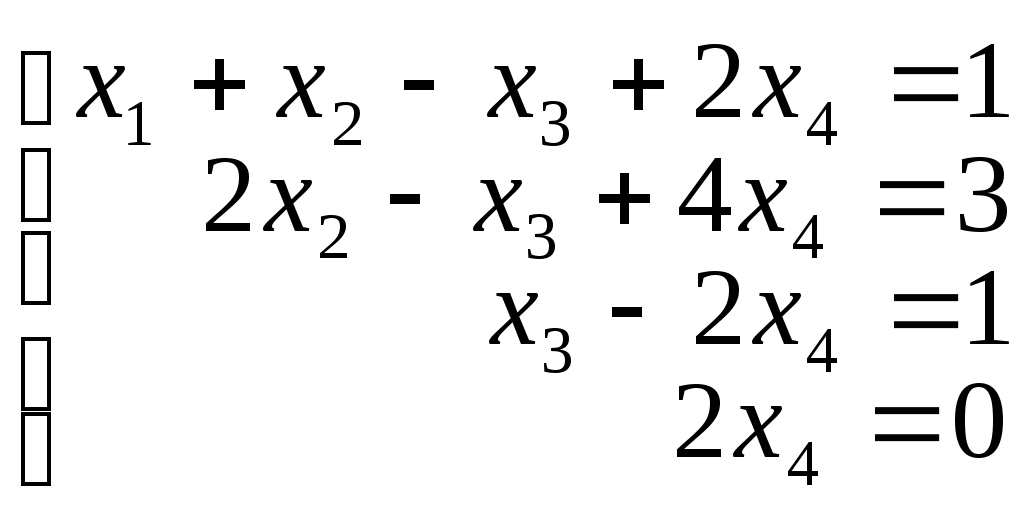
В этом случае система имеет единственное решение (0, 2, 1,0) (проверьте!)

в)

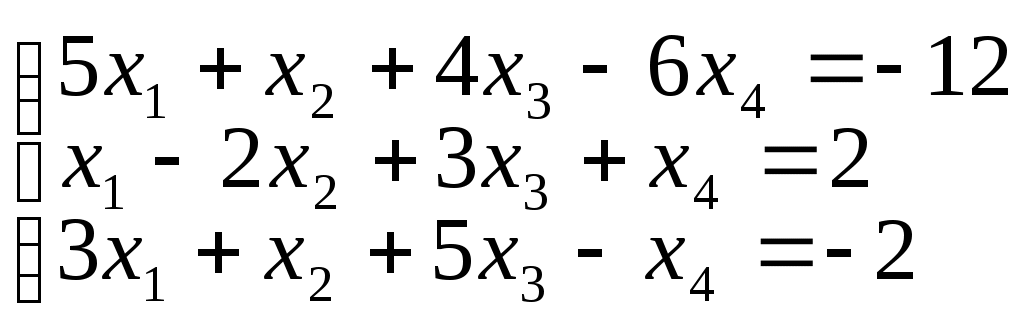
Решение.

B =





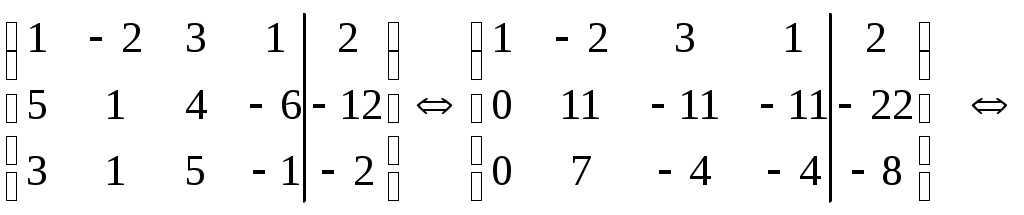
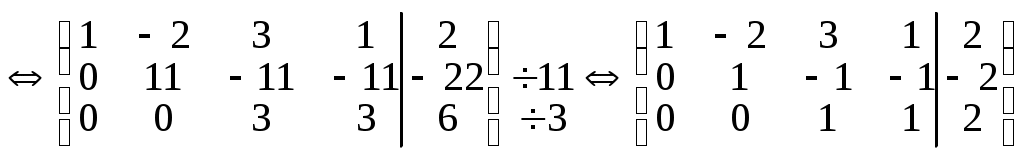
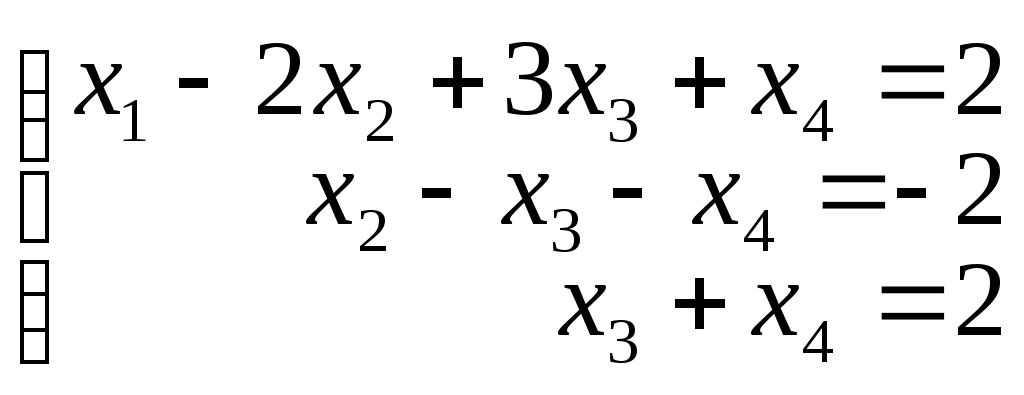
Система имеет множество решений. В этом случае поступают следующим образом: по числу оставшихся уравнений выбирают главные переменные. Пусть это будут х₁ х₂ х₃ . Остальные будут свободными, то есть х₄. Выразим главные переменные через свободные (поднимаясь по системе снизу вверх):

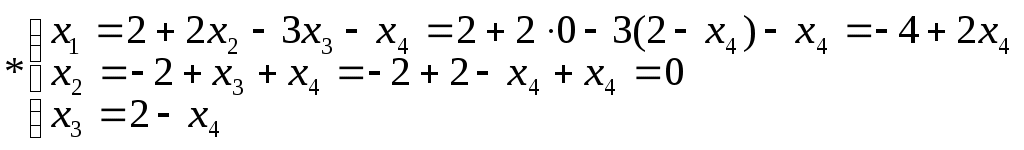
Возьмём для свободного переменного произвольное числовое значение, тогда, снова поднимаясь по системе * снизу вверх, получим однозначно определенные значения для главных переменных. Пусть x

---