ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1441
Скачиваний: 4
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
найменших
квадратів
згоду
з
відповідними
дійсності
значеннями
,
а
невідомі
функції
q
(
τ
)
інтегральних
рівнянь
шукаємо
як
( )
( )
∑
ρ
=
ρ
τ
ω
=
τ
0
j
r
j
j
r
C
Q
,
(20)
де
многочлени
( )
{
}
(
)
ρ
=
τ
ω
,
,
2
,
1
,
0
,
K
j
r
j
ортогональні
на
системі
точок
T
.
Зокрема
,
якщо
(20)
складається
з
цілих
ненегативних
мір
змінної
τ
,
тобто
( )
( )
( )
( )
,
,
,
,
,
,
1
2
2
1
0
K
K
ρ
ρ
τ
=
τ
ω
τ
=
τ
ω
τ
=
τ
ω
=
τ
ω
то
( )
ρ
ρ
ρ
τ
+
+
τ
+
=
τ
C
C
C
Q
K
1
0
є
звичайний
поліном
міри
ρ
.
Для
шуканого
многочлена
( )
r
Q
τ
ρ
повинна
виконуватись
умова
( ) ( )
[
]
∑
=
∗
=
−
=
Ω
n
r
r
r
ρ
ρ
τ
q
τ
Q
0
2
min
. (21)
Замінюючи
і
на
r
q
s
f
( )
τ
ρ
Q
і
( )
s
U
τ
ρ
,
помноживши
обидві
частини
(18)
на
і
проводячи
підсумовування
по
r
від
0
до
n
отримуємо
систему
рівнянь
для
невідомих
коефіцієнтів
:
( )
r
j
τ
ω
j
C
(
∑
ρ
=
ρ
=
=
⋅
0
,
,
,
2
,
1
,
0
,
j
k
j
k
j
k
a
C
A
K
)
,
(22)
( ) ( )
∑∑
=
=
τ
ω
⋅
τ
ω
=
n
r
n
S
r
r
j
S
r
k
j
K
A
0
0
,
,
.
(23)
Її
і
слід
вирішувати
чисельно
.
Вона
має
значно
менший
порядок
,
ніж
початкова
система
,
і
добре
обумовлена
[2, 6].
По
знайдених
з
(8)
визначаємо
невідому
функцію
,
припускаючи
.
j
C
( )
r
r
Q
q
τ
≈
ρ
Міра
ρ
ортогональних
многочленів
,
що
апроксимують
задану
і
шукану
функцію
,
аналогічний
параметру
регуляризації
[2].
Оптимальне
значення
міри
ортогонального
многочлена
,
що
апроксимує
розв
’
язок
інтегрального
рівняння
,
вибираємо
з
умови
мінімуму
функціонала
0
ρ
=
ρ
( )
[
]
ρ
−
−
τ
=
Ω
∑
=
ρ
∗
ρ
n
q
Q
n
r
r
r
0
2
. (24)
Таким
чином
,
у
разі
використання
ортогональних
многочленів
обчислення
параметрів
і
виконується
по
готових
формулах
,
які
позбавляють
від
необхідності
розв
’
язку
системи
нормальних
рівнянь
.
k
a
j
C
8’2012
160
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
Організація
охолодження
конструкції
камер
згоряння
рідинних
ракетних
двигунів
є
одним
із
найважливіших
питань
проектування
та
в
порівнянні
з
іншими
видами
теплових
машин
ускладнюється
тим
,
що
теплові
процеси
протікають
при
високих
температурах
(3000–4000) K
та
тиску
.
Оскільки
високотемпературні
продукти
згоряння
рухаються
по
камері
з
дуже
великою
швидкістю
,
то
різко
зростають
коефіцієнт
конвективної
тепловіддачі
від
гарячих
продуктів
згоряння
до
стінок
камери
та
конвективні
теплові
потоки
q
k
,
що
досягають
в
критичному
перерізі
сопла
до
7·10
7
Вт
/
м
2
.
Крім
того
,
теплообмін
в
конструкції
характеризується
високим
рівнем
радіації
в
камері
,
що
призводить
до
великих
променевих
теплових
потоків
q
л
.
Внаслідок
потужних
сумарних
конвективних
та
променевих
теплових
потоків
до
стінки
камери
її
температура
може
досягати
значень
вище
(1000–1500)
°
С
.
Величина
цих
потоків
визначається
значеннями
режимних
параметрів
,
складом
продуктів
згоряння
у
ядрі
газового
потоку
та
в
пристіночному
шарі
,
а
також
температурою
внутрішньої
поверхні
конструкції
.
Внаслідок
зміни
діаметру
проточної
частини
по
довжині
тепловідвід
від
продуктів
згоряння
виявляється
нерівномірним
.
Нерівномірним
є
також
розподіл
температури
по
периметру
,
що
зумовлено
зміною
складу
продуктів
згоряння
.
Коефіцієнт
тепловіддачі
від
продуктів
згоряння
визначається
з
урахуванням
спільної
дії
конвективного
та
променевого
теплових
потоків
у
відповідному
перерізі
конструкції
вузла
за
значеннями
параметрів
(
тиск
,
склад
і
температура
продуктів
згоряння
у
ядрі
газового
потоку
та
в
пристіночному
шарі
)
на
сталому
режимі
експлуатації
[2, 3].
Час
виходу
розглянутих
конструкцій
на
сталий
тепловий
режим
може
виявитися
навіть
більше
часу
їх
роботи
при
експлуатації
.
В
таких
умовах
задача
визначення
теплового
стану
в
період
роботи
зводиться
до
розрахунку
прогріву
їх
під
впливом
високотемпературних
продуктів
згоряння
[3].
У
частині
сопла
,
що
розширюється
протікає
процес
конвективного
теплообміну
між
газовим
потоком
,
що
має
велику
швидкість
(
М
> 1)
та
стінкою
сопла
.
Для
розрахунку
цього
випадку
тепловіддачі
в
літературі
пропонується
формула
:
11
,
0
2
39
,
0
4
,
0
8
,
0
2
1
1
Pr
Re
029
,
0
Nu
⎟
⎠
⎞
⎜
⎝
⎛
µ
−
+
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
⋅
=
k
r
T
T
r
w
w
wx
wx
.
(25)
У
якості
визначальної
температури
приймається
відповідно
:
–
температура
у
ядрі
,
що
визначається
з
термодинамічного
розрахунку
камери
згоряння
;
–
температура
внутрішньої
стінки
камери
згоряння
;
f
T
w
T
(
)
w
f
m
T
T
T
+
⋅
=
5
,
0
та
(
)
w
r
m
T
T
T
+
⋅
=
5
,
0
;
і
–
відповідно
температура
продуктів
згоряння
та
газової
стінки
в
К
.
r
T
w
T
Безпосередньо
виміряти
значення
температури
(
( )
τ
,
y
T
w
)
та
теплового
потоку
(
)
на
внутрішній
стінки
камери
згоряння
в
більшості
випадків
неможливо
,
тому
необхідно
використовувати
непрямі
методи
їх
визначення
.
Значення
та
(
τ
,
y
q
w
)
)
(
τ
,
y
T
w
( )
τ
,
y
q
w
можливо
визначити
за
вимірюваними
при
експерименті
температурами
усередині
або
на
поверхні
стінки
,
вирішуючи
обернені
задачі
теплопровідності
.
При
стендовій
обробці
камер
згорання
робиться
вимір
температури
поверхні
в
перерізах
відповідних
корпусів
вузлів
(
рис
. 1).
На
поверхні
в
перерізі
розташовується
по
дві
точки
виміру
,
розташованих
в
діаметрально
протилежних
точках
периметру
8’2012
161
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
корпусу
.
Експериментальні
дані
і
результати
розв
’
язку
оберненої
теплової
задачі
для
системи
тришарових
пластин
приведені
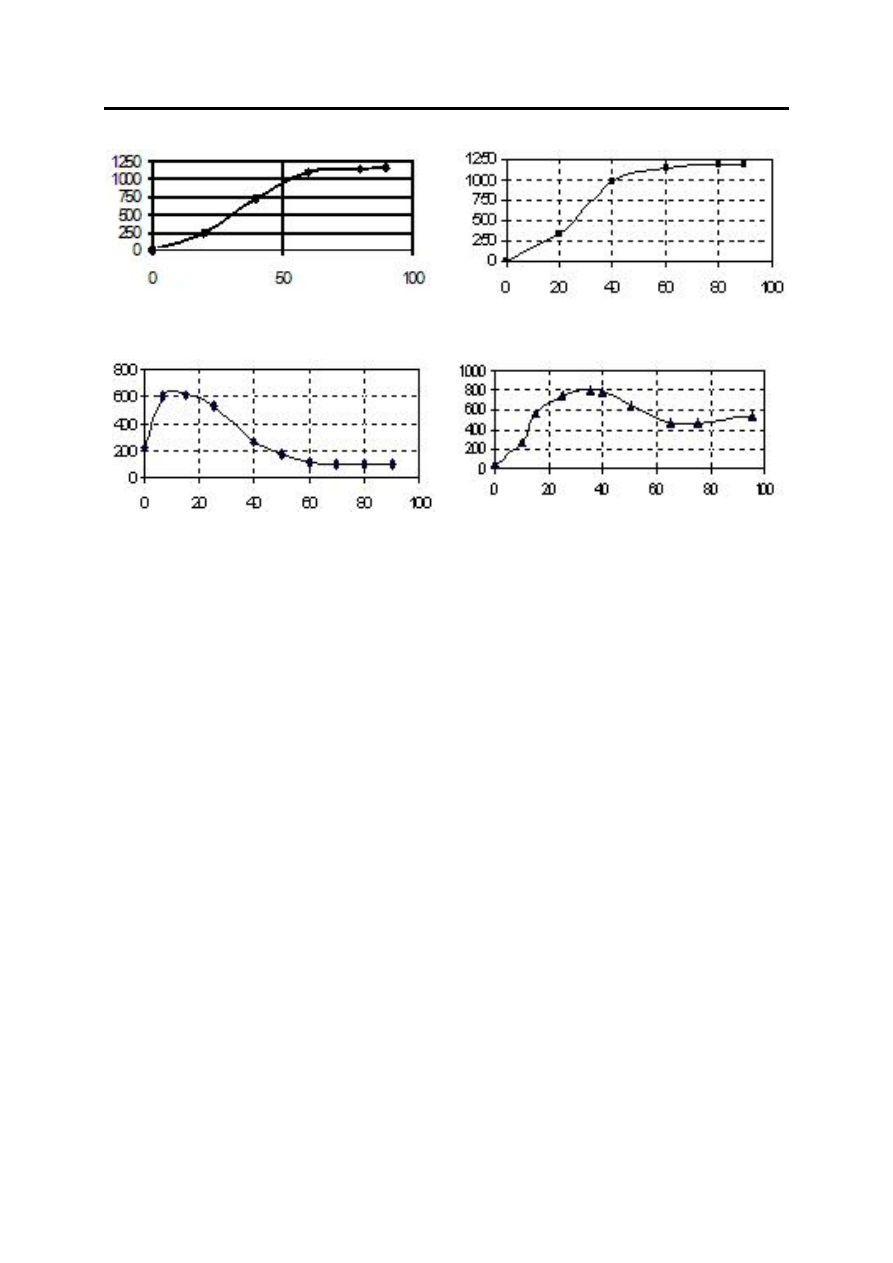
на
рис
. 2
а
–
г
.
Невід
’
ємною
частиною
будь
-
якого
реального
теплового
експерименту
є
стохастичність
спостережуваних
величин
.
Стохастичність
процесу
визначається
різноманітними
факторами
.
Зокрема
,
в
реальних
умовах
механічні
характеристики
,
теплофізичні
та
геометричні
параметри
та
температура
,
що
вимірюється
є
випадковими
величинами
із
-
за
дефектів
виробництва
,
технології
виготовлення
,
забруднення
поверхні
,
погрішності
виміру
та
обробки
експериментальної
інформації
та
інших
факторів
.
Отже
,
ймовірна
природа
величин
,
що
спостерігаються
в
реальному
експерименті
,
призводить
до
випадкового
функціонального
характеру
та
температурного
поля
.
Рис
. 1.
Розрахункова
схема
системи
тришарових
пластин
Розв
’
язок
граничних
ОЗТ
для
багатошарових
конструкцій
є
багато
параметричною
задачею
.
Тут
наряду
з
випадковим
характером
експериментальної
температури
великий
розкид
існує
і
в
інших
параметрах
:
теплофізичні
характеристики
,
геометричні
розміри
системи
та
місце
установки
датчиків
температури
,
характеристики
неідеального
теплового
контакту
.
Відомо
,
що
устаткування
,
що
використовується
при
проведенні
натурних
вимірювань
температур
мають
достатньо
високий
клас
точності
,
а
саме
:
приладова
погрішність
вимірювань
температур
в
діапазоні
їх
коливань
від
0
до
600
°
С
знаходиться
в
межах
3
°
С
,
а
сумарна
погрішність
вимірювань
дорівнює
(1–2) %
температури
,
що
вимірюється
.
В
деяких
випадках
при
організації
спеціальної
системи
регістрації
та
вимірювань
температур
загальна
погрішність
вимірювань
температури
може
бути
зведена
до
мінімуму
(
не
більш
ніж
1
°
С
).
Одним
з
методів
розв
’
язку
оберненої
задачі
теплопровідності
є
метод
статистичних
випробувань
Монте
-
Карло
[3, 4],
котрий
полягає
в
статистичному
моделюванні
аналітичних
розв
’
язків
обернених
задач
теплопровідності
з
урахуванням
випадкового
характеру
вихідних
даних
.
Використовуючи
метод
Монте
-
Карло
можливо
досліджувати
вплив
погрішностей
вихідної
інформації
(
геометричні
розмірі
,
місце
установки
температурного
датчику
,
теплофізичні
характеристики
,
вимірювання
та
обробка
експериментальною
температури
внутрішніх
точок
тіла
)
на
розв
’
язок
оберненої
задачі
теплопровідності
.
Коридор
помилок
відновленого
розв
’
язку
можливо
визначити
по
результатам
статистичної
обробки
отриманих
реалізацій
.
Крім
того
,
процедура
Монте
–
Карло
дозволяє
розглядати
вплив
кожної
вхідної
величини
на
розв
’
язок
оберненої
задачі
теплопровідності
.
Розрахунки
для
тришарової
пластини
показали
,
що
похибка
в
завданні
експериментальної
температури
до
5 %
викликає
максимальні
відхилення
температури
поверхні
до
10 %
на
тимчасовому
інтервалі
0–55
с
,
а
на
іншій
тимчасовій
ділянці
до
5%,
теплового
потоку
– 20 %
і
10 %
відповідно
.
8’2012
162
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
T
,
°
C
τ
, c
T
W
,
°
C
τ
, c
а
)
б
)
q
3
,
Вт
/
м
2
τ
, c
α
,
Вт
/(
м
2
·
°
С
)
τ
, c
в
)
г
)
Рис
. 2.
Відновлені
краєві
умови
:
а
–
експериментальна
температура
f
2,
э
(
τ
);
б
–
температура
поверхні
T
3,
W
(1,
τ
);
в
–
тепловий
потік
q
3,
W
(1,
τ
);
г
–
коефіцієнт
тепловіддачі
α
Список
літератури
: 1.
Карташов
,
Э
.
М
.
Аналитические
методы
в
теории
теплопроводности
твердых
тел
[
Текст
] /
Э
.
М
.
Карташов
. –
М
.:
Высшая
школа
, 2001. – 540
с
.
2.
Алифанов
,
О
.
М
.
Обратные
задачи
как
методологическая
основа
идентификации
тепловых
математических
моделей
[
Текст
] /
О
.
М
.
Алифанов
//
Тепломассообмен
.
ММФ
. –
Минск
:
ИТМО
АНБ
, 2000. –
Т
. 3. –
С
. 3-13.
3.
Веселовский
,
В
.
Б
.
Решение
задач
нестационарной
теплопроводности
для
многослойных
плоских
тел
с
неидеальным
тепловым
контактом
[
Текст
] /
В
.
Б
.
Веселовский
//
Прикладные
вопросы
аэродинамики
летательных
аппаратов
. –
Киев
:
Наук
.
думка
, 1984. –
С
. 140-144.
4.
Веселовский
,
В
.
Б
.
Тепловые
режимы
составных
элементов
конструкций
летательных
аппаратов
[
Текст
] /
В
.
Б
.
Веселовский
//
Тепломассообмен
. –
Вычислительный
эксперимент
в
задачах
тепломассообмена
и
теплопередачи
. –
Минск
:
Институт
тепло
-
и
массообмена
АН
Беларуси
, 1996. –
Т
. 9. ––
С
. 37-41.
5.
Веселовский
,
В
.
Б
.
Температурные
поля
электрических
кабелей
при
воздействии
полей
различной
физической
природы
[
Текст
] /
В
.
Б
.
Веселовский
,
А
.
В
.
Берлов
,
Н
.
И
.
Белый
,
В
.
И
.
Ляшенко
//
Вісник
Дніпропетровського
університету
.
Сер
.
Механіка
. – 2001. –
Вип
. 5,
Т
. 1. –
С
. 73-83.
6.
Веселовский
,
В
.
Б
.
Определение
нестационарных
граничных
условий
на
огневых
стенках
корпусов
по
экспериментальным
замерам
температур
[
Текст
] /
В
.
Б
.
Веселовский
,
И
.
Н
.
Даценко
,
В
.
В
.
Никульникова
,
В
.
И
.
Ляшенко
//
Вісник
Дніпропетровського
університету
.
Сер
.
Механіка
. – 2002. –
Вип
. 6,
Т
. 1. –
С
. 102-110.
7.
Веселовский
,
В
.
Б
.
Нестационарное
температурное
поле
составных
элементов
конструкций
[
Текст
] /
В
.
Б
.
Веселовский
//
Математические
методы
тепломассопереноса
. –
Днепропетровск
:
Днепропетровский
гос
.
университет
, 1986. –
С
. 107-110.
8.
Веселовский
,
В
.
Б
.
Моделирование
влияния
полей
различной
физической
природы
на
тепловые
режимы
составных
элементов
конструкций
[
Текст
] /
В
.
Б
.
Веселовский
,
В
.
Ю
.
Клим
,
Н
.
И
.
Белый
//
Вісник
Дніпропетровського
університету
.
Сер
.
Механіка
. – 2002. –
Вип
. 6.,
Т
. 1. –
С
. 111-119.
©
Біляєва
В
.
В
.,
Берлов
О
.
В
.,
Клім
В
.
Ю
., 2012
Надійшла
до
редколегії
15.02.12
8’2012
163
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
УДК
621.05
Р
.
С
.
ВАРИБРУС
,
магистр
НТУ
«
ХПИ
»
СИНТЕЗ
СХЕМЫ
ПНЕВМОАГРЕГАТА
ПРОМЫШЛЕННОГО
РОБОТА
Предлагается
провести
синтез
схем
пневматического
манипулятора
двумя
методами
:
с
использованием
стандартной
позиционной
структуры
и
методом
полной
минимизации
стандартной
позиционной
структуры
.
Пропонується
провести
синтез
схем
пневматичного
маніпулятора
двома
методами
:
з
використанням
стандартної
позиційної
структури
та
методом
повної
мінімізації
стандартної
позиційної
структури
.
It was proposed to conduct the synthesis of charts of pneumatic manipulator two methods: with the use of
standard position structure and by the method of complete minimization of standard position structure.
В
данной
статье
проводиться
синтез
схем
пневматического
манипулятора
двумя
методами
:
с
использованием
стандартной
позиционной
структуры
и
методом
полной
минимизации
стандартной
позиционной
структуры
[1, 2].
Исполнительными
устройствами
автоматического
манипулятора
являются
пневматические
цилиндры
Ц
1
–
Ц
4
.
Исходное
положение
Ц
1
контролирует
конечный
выключатель
(
ВК
)
X
2
,
а
его
конечное
положение
–
X
3
.
Исходное
положение
Ц
2
контролирует
ВК
X
4
,
а
конечное
положение
–
X
5
.
Конечное
положение
Ц
3
контролирует
ВК
X
7
.
Исходное
положение
Ц
4
контролирует
ВК
X
8
,
а
его
конечное
положение
–
X
9
(
табл
. 1)
Цикл
работи
начинается
с
нажимания
на
кнопку
пуска
X
1
(
X
1
= 1)
при
этом
происходит
захват
заготовки
Z
1
= 1,
в
конечном
положении
цилиндр
Ц
1
воздействувет
на
конечный
выключатель
X
3
= 1
и
происходит
подъем
руки
Z
2
= 1.
Затем
по
сигналу
X
5
= 1
от
ВК
происходит
поворот
руки
(
Z
3
= 1).
В
конце
хода
Ц
3
воздействует
на
ВК
по
сигналу
X
7
= 1
и
корпус
манипулятора
поворачивается
(
Z
4
= 1),
заготовка
устанавливается
на
указанное
место
.
Далее
по
сигналу
X
9
= 1
происходит
разжим
заготовки
1
1
=
Z
.
По
сигналу
ВК
X
2
= 1
корпус
манипулятора
поворачивается
назад
1
4
=
Z
.
Поворот
руки
назад
)
1
(
3
=
Z
осуществляется
по
сигналу
X
8
= 1,
далее
по
сигналу
1
7
=
X
происходит
опускание
руки
1
2
=
Z
.
Кнопка
Р
стоп
устанавливает
все
исполнительный
устройства
и
все
распределители
командоаппарата
в
исходное
положение
.
Таблица
1
Взаимодействие
входных
и
исполнительных
устройств
Входные
сигналы
Наименование
операции
Выходные
сигналы
начальные
конечные
Захват
заготовки
Z
1
X
2
X
3
Подъем
руки
Z
2
–
X
5
Поворот
руки
Z
3
–
X
7
Поворот
корпуса
Z
4
X
8
X
9
Для
построения
схемы
с
использованием
стандартной
позиционной
структуры
(
рис
. 2)
воспользуемся
формулой
:
8’2012
164