ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1439
Скачиваний: 4
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
1
−
=
i
i
i
y
p
S
, (1)
где
S
i
–
сигнал
включения
i
-
го
элемента
памяти
(
ЭП
);
p
i
–
входной
набор
,
который
переводи
систему
из
одного
состояния
в
другое
в
i
-
м
переходе
;
y
i
–1
–
выход
ЭП
в
предыдущем
переходе
i
–1 (
рис
. 1).
Функции
выходов
Z
=
f
(
y
)
зависят
только
от
внутренних
состояний
и
не
зависят
от
входных
наборов
Z
m
=
y
i
,
где
Z
m
–
функция
выхода
m.
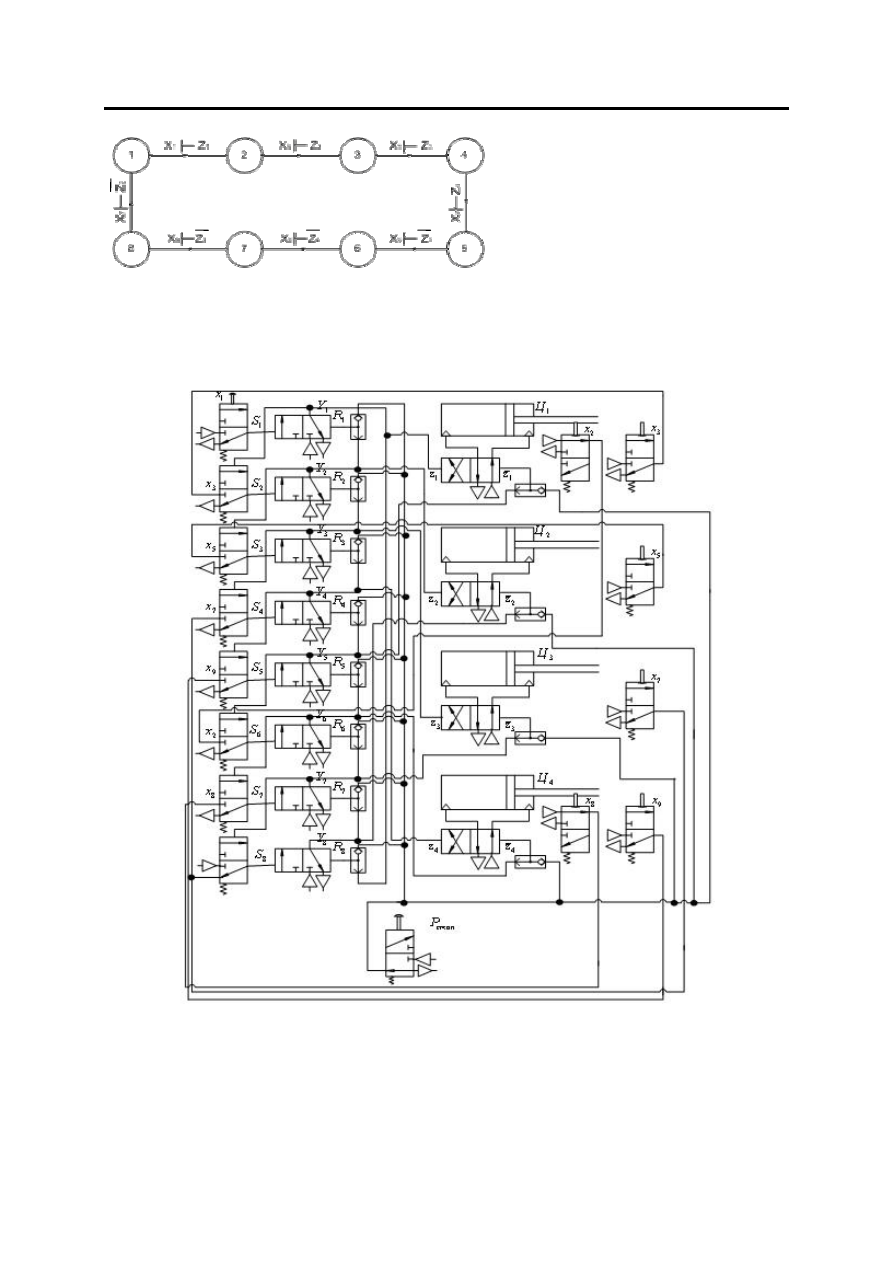
Рис
. 1.
Граф
операций
,
который
описывает
условия
работы
системы
управления
Рис
. 2.
Пневматическая
схема
управления
промышленным
роботом
реализованная
с
использованием
стандартной
позиционной
структуры
Если
входная
последовательность
содержит
одинаковые
наборы
,
то
проводим
её
разбиение
на
π
блоки
,
не
содержащие
одинаковые
входные
наборы
.
Разбиение
8’2012
165
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
осуществляется
по
циклу
с
какого
-
либо
набора
,
с
учетом
,
чтобы
одинаковые
наборы
не
были
последними
в
блоке
.
Если
при
разбиении
получилось
два
блока
,
то
используется
один
элемент
памяти
с
двумя
выходами
–
прямым
и
инверсным
(
y
y
,
)
.
В
случае
отсутствия
одинаковых
наборов
разбиение
не
нужно
.
Дальше
переходим
к
минимизации
логических
уравнений
на
основании
матрицы
соответствий
(
МС
).
Использование
МС
позволяет
синтезировать
систему
уравнений
независимо
от
числа
входов
и
выходов
,
поскольку
размерность
МС
определяется
числом
переходов
системы
управления
.
Строки
МС
соответствуют
входным
наборам
Р
с
учетом
сигналов
у
с
выходов
ЭП
,
а
столбцы
–
сигналам
,
которые
вызывают
переходы
управляющего
аппарата
.
На
пересечении
строки
i
и
столбца
j
ставится
единица
,
если
входные
сигналы
,
которые
соответствуют
столбцу
j
,
входят
во
входной
набор
,
который
соответствует
строке
i
,
в
противном
случае
ставиться
0.
Противоречивые
единицы
обводятся
в
круг
.
Единицы
,
соответствующие
переходам
,
выделяют
«
жирным
»
шрифтом
.
В
общем
случае
для
удаления
противоречивых
единиц
сигналы
сканируемого
столбца
необходимо
удлинить
сигналами
,
присутсвующими
на
данном
переходе
и
отсутствующими
в
переходе
,
где
находиться
противоречивая
единица
.
Таких
сигналов
может
быть
несколько
,
но
нужно
стремиться
к
их
минимальному
числу
.
Логические
уравнения
включения
исполнительных
устройств
и
ЭП
получаем
из
выражений
,
записанных
сверху
МС
,
для
соответственного
«
жирной
»
единице
выхода
.
Таблица
2
Матрица
соответствий
X
1
X
3
X
5
X
3
X
7
X
3
X
9
X
2
X
8
X
2
2
7
X
X
X
2
X
4
X
8
0 0 0 0 0 1 1 1
∅
X
1
X
2
X
4
X
8
1
0 0 0 0 1 1 1
1
Z
X
3
X
4
X
8
0
1
0 0 0 0 1
2
Z
X
5
X
3
X
8
0 1
1
0 0 0
3
Z
X
7
X
3
X
5
X
8
0 1 1
1
0 0
0
4
Z
X
9
X
3
X
5
X
7
0 1 1 1
1
0 0 0
1
Z
X
2
X
5
X
7
X
9
0 0 1
1
1
0 0
4
Z
X
8
X
2
X
5
X
7
0 0
0 1
1
0
3
Z
8
2
5
7
X
X
X
X
0 0
0 0 1 1
1
2
Z
1
1
1
1
1
1
1
1
По
матрице
соответствий
(
табл
. 2)
получаем
систему
уравнений
:
8’2012
166
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
;
;
;
;
;
3
5
3
2
7
2
3
2
9
1
1
1
X
X
Z
X
X
Z
X
Z
X
Z
X
Z
=
=
=
=
=
.
;
;
2
4
3
7
4
8
2
3
X
Z
X
X
Z
X
X
Z
=
=
=
(2)
Таким
образом
,
очевидно
,
что
метод
полной
минимизации
стандартной
позиционной
структуры
является
более
эффективным
,
а
именно
позволяет
минимизировать
число
аппаратов
,
что
способствует
снижению
стоимости
пневмоагрегата
,
повышению
быстродействия
,
упрощению
наладки
и
обслуживания
.
Это
можно
увидеть
на
рисунке
(
рис
. 3).
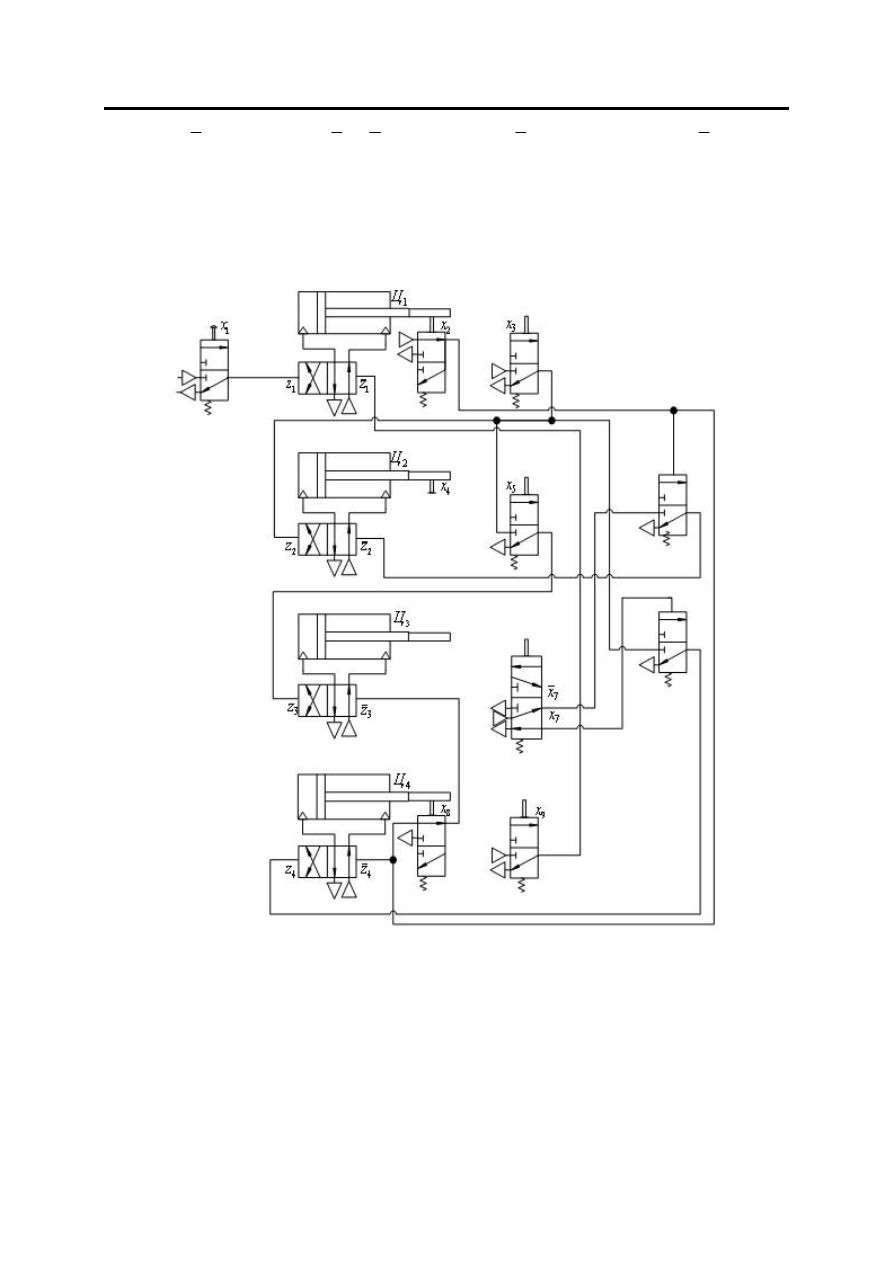
Рис
. 3.
Минимизированная
пневматическая
схема
управления
промышленным
роботом
Список
литературы
: 1.
Черкашенко
,
М
.
В
.
Автоматизац
i
я
проектування
систем
г
i
дро
–
и
пневмопривод
i
в
с
дискретним
управл
i
нням
[
Текст
] /
М
.
В
.
Черкашенко
. –
М
.:
Машиностроение
, 1992.
2.
Черкашенко
,
М
.
В
.
Структурный
синтез
и
анализ
схем
гидропневмоавтоматики
[
Текст
] /
М
.
В
.
Черкашенко
.–
Харк
i
в
:
НТУ
«
ХПИ
», 2007. – 297
с
.
©
Варибрус
Р
.
С
., 2012
Поступила
в
редколлегию
15.02.12
8’2012
167
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
УДК
699.86
В
.
А
.
ВОЛОЩУК
,
канд
.
техн
.
наук
;
доц
.
Національного
Університету
Водного
Господарства
та
Природокористування
,
Рівне
ВПЛИВ
ЗМІННОСТІ
ПОГОДНО
-
КЛІМАТИЧНОГО
ЧИННИКА
НА
НЕВИЗНАЧЕНІСТЬ
ПРИ
ВИБОРІ
ТЕРМІЧНОГО
ОПОРУ
ОГОРОДЖУВАЛЬНОЇ
КОНСТРУКЦІЇ
БУДИНКУ
В
статье
показано
,
что
учет
вероятностного
характера
изменения
количества
градусо
-
суток
в
многолетнем
сечении
может
существенным
образом
повлиять
на
неопределенность
параметров
выбора
сопротивления
теплопередачи
оградительной
конструкции
дома
.
В
статті
показано
,
що
урахування
імовірнісного
характеру
зміни
кількості
градусо
-
діб
у
багаторічному
перерізі
може
істотно
вплинути
на
невизначеність
параметрів
вибору
опору
теплопередачі
огороджувальної
конструкції
будинку
.
It is shown, that consideration of stochastic change of heating degree days over years can substantially affects
the vagueness of parameters of choosing thermal resistance of building envelope.
Зважаючи
на
те
,
що
Україна
характеризується
високим
рівнем
питомих
тепловтрат
існуючих
будинків
,
суттєвого
зменшення
затрат
на
їх
опалення
можна
досягти
,
зокрема
,
шляхом
підвищення
термічного
опору
зовнішнього
огородження
.
Підвищення
теплозахисту
огороджувальних
конструкцій
вимагає
додаткових
капіталовкладень
.
Інвестиційна
привабливість
таких
вкладень
сьогодні
визначається
із
використанням
чотирьох
основних
загальноприйнятих
у
світовій
економічній
практиці
показників
[1]:
чистий
дисконтований
дохід
,
індекс
дохідності
,
внутрішня
норма
дохідності
,
термін
окупності
,
які
є
взаємопов
’
язаними
.
На
вибір
теплозахисту
будинку
впливає
цілий
ряд
факторів
.
Одним
із
них
є
погодно
-
кліматичний
чинник
–
кількість
градусо
-
діб
.
В
існуючих
підходах
,
при
вирішені
задачі
обґрунтування
значення
термічного
опору
огороджувальної
конструкції
будинку
кількість
градусо
-
діб
для
конкретної
території
розміщення
об
’
єкта
приймається
постійною
і
рівною
осередненому
в
багаторічному
перерізі
значенню
даної
величини
[2, 3]
без
урахування
коливань
цих
параметрів
як
в
багаторічному
перерізі
,
так
і
всередині
року
,
що
є
сьогодні
недостатнім
.
Метою
роботи
є
розробка
та
перевірка
методу
визначення
впливу
природної
сезонної
мінливості
погодно
-
кліматичних
чинників
у
багаторічному
перерізі
на
невизначеність
параметрів
вибору
термічного
опору
огороджувальної
конструкції
.
У
літературі
[4]
пропонується
декілька
підходів
,
на
основі
яких
можна
вибирати
оптимальні
рішення
при
управлінні
природно
-
технічними
системами
з
урахуванням
стохастичної
зміни
метеорологічних
режимів
.
Розглянемо
так
званий
байесівський
підхід
.
При
описанні
множин
погодно
-
кліматичних
умов
{ }
D
D
=
Ω
як
і
при
описанні
дій
зі
сторони
,
наприклад
,
системи
теплозабезпечення
будівель
{ }
R
R
=
Ω
може
бути
два
випадки
.
Перший
характеризується
тим
,
що
множини
d
Ω
та
R
Ω
дискретні
і
включають
в
себе
кінцеву
кількість
елементів
,
, ...,
та
,
, ...,
,
що
відповідають
різним
погодним
умовам
та
режимам
роботи
систем
теплозабезпечення
.
Другий
випадок
означає
,
що
множини
та
1
D
2
D
m
D
1
R
2
R
n
R
D
Ω
R
Ω
неперервні
.
8’2012
168
ЕНЕРГЕТИЧНІ
ТА
ТЕПЛОТЕХНІЧНІ
ПРОЦЕСИ
Й
УСТАТКУВАННЯ
Маючи
дані
про
характер
множин
D
Ω
та
R
Ω
,
можна
побудувати
функцію
(
)
R
,
D
u
u
=
, (1)
яка
показує
,
який
буде
ефект
при
прийнятті
деякого
рішення
і
здійсненні
погодних
умов
R
R
Ω
∈
D
D
Ω
∈
.
Ця
функція
може
розглядатися
як
функція
доходу
,
якщо
мова
іде
про
позитивний
ефект
,
функція
витрат
,
якщо
описуються
витрати
тощо
.
Отже
,
для
випадку
довгострокових
рішень
при
управлінні
природно
-
технічними
системами
(
наприклад
,
при
виборі
теплозахисту
огороджувальної
конструкції
),
оптимально
використати
кліматологічну
інформацію
можна
наступним
чином
.
Якщо
через
позначити
кліматологічну
стратегію
управління
,
смисл
якої
полягає
у
прийнятті
одного
і
того
ж
рішення
R
j
cl
s
j
,
то
,
згідно
байесівського
підходу
,
осереднене
значення
функції
(1)
при
вибраній
стратегії
буде
визначатися
за
формулою
j
cl
s
(
)
( )
∑
=
=
m
i
i
j
i
cl
D
P
R
D
u
U
j
1
,
, (2)
де
–
природна
повторюваність
відповідного
метеофактора
або
комплексного
показника
,
що
характеризує
погодно
-
кліматичні
умови
у
багаторічному
перерізі
.
(
i
D
P
)
Процедура
пошуку
кліматологічно
оптимальної
стратегії
заключається
в
розрахунку
величин
j
cl
U
для
всіх
n
j
,
1
=
та
знаходження
серед
них
екстремуму
.
Та
стратегія
,
що
відповідає
екстремальному
значенню
j
cl
U
і
буде
,
згідно
байесівського
підходу
,
кліматологічно
оптимальною
.
Для
неперервних
моделей
задача
пошуку
кліматологічно
оптимальної
байесівської
стратегії
полягає
в
знаходженні
такого
постійного
рішення
R
j
,
що
не
залежить
від
конкретного
стану
погоди
,
при
якому
середнє
в
статистичному
смислі
значення
функції
( )
( )
∫
=
x
,
dx
x
f
R
x
u
U
j
(3)
досягає
екстремального
значення
або
задовольняє
відповідній
умові
.
В
цій
формулі
через
f
(
x
)
позначений
закон
розподілу
метеофактора
(
або
комплексу
метеофакторів
),
що
характеризує
особливості
клімату
території
розміщення
об
’
єкта
.
В
багатьох
випадках
важливо
при
оптимізації
управління
об
’
єкта
(
системи
),
робота
якого
залежить
від
погодно
-
кліматичного
чинника
,
є
коливання
доходів
,
втрат
тощо
,
викликаних
дією
некерованих
метеорологічних
факторів
.
Очевидно
,
що
чим
більші
ці
коливання
,
тим
вища
невизначеність
рішень
,
що
приймаються
,
і
тим
менша
можливість
завчасної
компенсації
наступних
відхилень
.
Для
зниження
«
метеорологічної
»
нестійкості
прийнятих
рішень
можна
вибрати
стратегію
,
при
якій
мінімізується
дисперсія
ефекту
від
прийнятого
рішення
[4]
(
)
(
)
( )
( )
min
,
,
1
2
1
→
⎥
⎦
⎤
⎢
⎣
⎡
−
=
∑
∑
=
=
m
i
i
m
i
i
j
i
j
i
s
D
P
D
P
R
D
u
R
D
u
D
(4)
або
8’2012
169