ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1761
Скачиваний: 2
Р
АЗДЕЛ
5
100
.
/
1
0
1
0
2
0
1
0
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ −
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
σ
σ
σ
σ
x
x
Ф
x
x
Ф
x
x
Ф
x
x
Ф
p
m
Решим
последнее
равенство
относительно
x
m
–
основной
характеристики
прочности
массива
:
(
)
.
1
arg
0
1
0
2
0
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
σ
σ
σ
x
x
p
Ф
x
x
Ф
p
Ф
x
x
m
(5.15)
Полученная
формула
прочности
породного
массива
должна
определиться
относительно
статистических
характеристик
для
усеченного
нормального
зако
-
на
распределения
,
т
.
е
.
в
формуле
(5.15)
вместо
x
0
необходимо
взять
величину
M(x)
из
(5.11),
а
вместо
σ
соответственно
D
из
(5.14).
Получим
( )
(
)
.
1
arg
0
1
0
2
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛ −
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
D
х
х
рФ
D
х
х
Ф
р
Ф
D
x
M
x
m
Поделив
все
члены
полученного
выражения
на
математическое
ожидание
M(x)
,
найдем
формулу
для
определения
коэффициента
структурного
ослабле
-
ния
:
[
]
⎟
⎠
⎞
⎜
⎝
⎛ −
+
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
=
D
х
х
рФ
D
x
x
Ф
p
Ф
k
c
0
1
0
2
1
arg
1
η
.
(5.16)
Таким
образом
,
получены
формулы
,
позволяющие
определить
расчетную
прочность
породного
массива
и
коэффициент
структурного
ослабления
,
пока
-
зывающий
,
насколько
необходимо
уменьшить
прочность
горной
породы
,
най
-
денную
при
испытании
выборки
образцов
как
математическое
ожидание
усе
-
ченного
нормального
закона
,
чтобы
иметь
расчетное
значение
прочности
.
Уро
-
вень
надежности
полученных
оценок
определяется
заданием
вероятности
p
,
ко
-
торая
зависит
от
технической
или
производственной
значимости
проектируе
-
мого
объекта
.
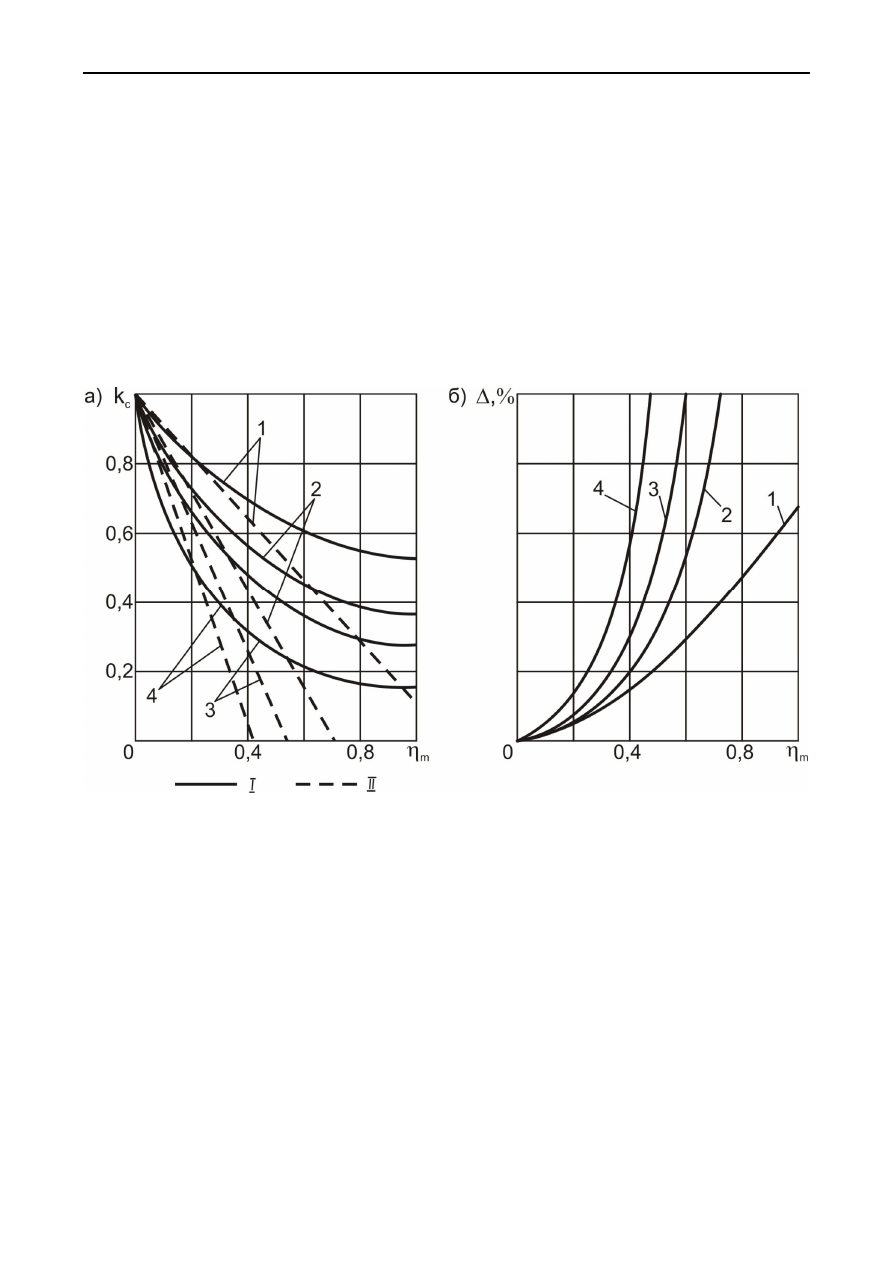
На
рис
. 5.3
приведены
графики
,
показывающие
,
как
зависит
ошибка
,
возникающая
при
использовании
нормального
закона
распределения
вместо
усеченного
нормального
закона
,
более
адекватно
описывающего
реаль
-
О
ПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА СТРУКТУРНОГО ОСЛАБЛЕНИЯ НА ОСНОВЕ ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ МОДЕЛЕЙ
101
ный породный массив. Из графиков следует, что в зависимости от уровня на-
дежности, при коэффициенте вариации, не превышающем 0,2-0,3, ошибка со-
ставляет 10-13% и в этих условиях можно применять нормальный закон рас-
пределения и вытекающие из него более простые зависимости. При более же
высоком уровне неоднородности породного массива ошибка становится суще-
ственной и следует использовать зависимости (5.15), (5.16), полученные на ос-
нове усеченного нормального закона распределения.
Рис. 5.3. Зависимость коэффициента структурного ослабления (а) и относи-
тельной ошибки вычисления (б) от относительной вариации прочности и
уровня надежности: I –усеченный нормальный закон распределения; II – нор-
мальный закон распределения; 1,2,3,4 – р=0,8; 0,9; 0,95; 0,99 соответственно
Практическое использование усеченного нормального распределения свя-
зано только с одним неудобством: для определения параметров теоретического
распределения кроме средней выборочной и выборочной дисперсии (именно
эти величины приводят исследователи как результат статистической обработки
стандартных испытаний образцов) необходимо располагать крайними выбо-
Р
АЗДЕЛ
5
102
рочными значениями
x
1
и
x
2
, которые, будучи полученными только из одной
серии испытаний, не являются несмещенными оценками своих теоретических
аналогов.
Нормальный закон распределения удовлетворительно описывает только те
величины, вариация которых не превышает 33 % (это вытекает из правила
«трех сигм»). Обычно для результатов лабораторного опробования образцов
большой разброс данных не характерен. Вариация прочности образцов при
этом не превосходит 30-35%, а статистическое распределение, построенное по
выборке, близко к нормальному.
Так, большой объем испытаний образцов для углевмещающих пород Дон-
басса был выполнен в лабораториях Национального горного университета. Гис-
тограммы относительных частот значений прочности образцов пород приведе-
ны в Приложении Б.
Для статистических данных были определены эмпирические начальные
k
m
и центральные
k
моменты
распределения:
,
1
1
n
i
k
i
B
k
R
n
m
(5.17)
,
1
1
1
n
i
k
i
B
k
m
R
n
(5.18)
где
B
n
– объем выборки,
k
– порядок момента,
i
R
– значения прочности образ-
цов.
С центральными моментами второго, третьего и четвертого порядков свя-
заны нормированные показатели асимметрии
1
и эксцесса
2
:
;
2
/
3
2
3
1
.
2
2
4
2
(5.19)
Обобщенные результаты обработки статистических данных в виде квадра-
та показателя асимметрии
1
и показателя островершинности
2
, сведены в
таблицу 5.1.
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
103
Таблица
5.1
Параметры
статистического
распределения
Параметры
распределения
Марки
углей
Вмещающие
породы
2
1
β
2
β
Д
-
ДГ
Аргиллит
Алевролит
Песчаник
0,261
0,336
0,213
3,099
2,970
2,421
Г
-
ГЖ
Аргиллит
Алевролит
Песчаник
0,637
0,545
0,470
2,623
2,875
3,123
Ж
,
КЖ
,
ОС
Аргиллит
Алевролит
Песчаник
1,043
0,336
0,514
5,029
2,970
3,003
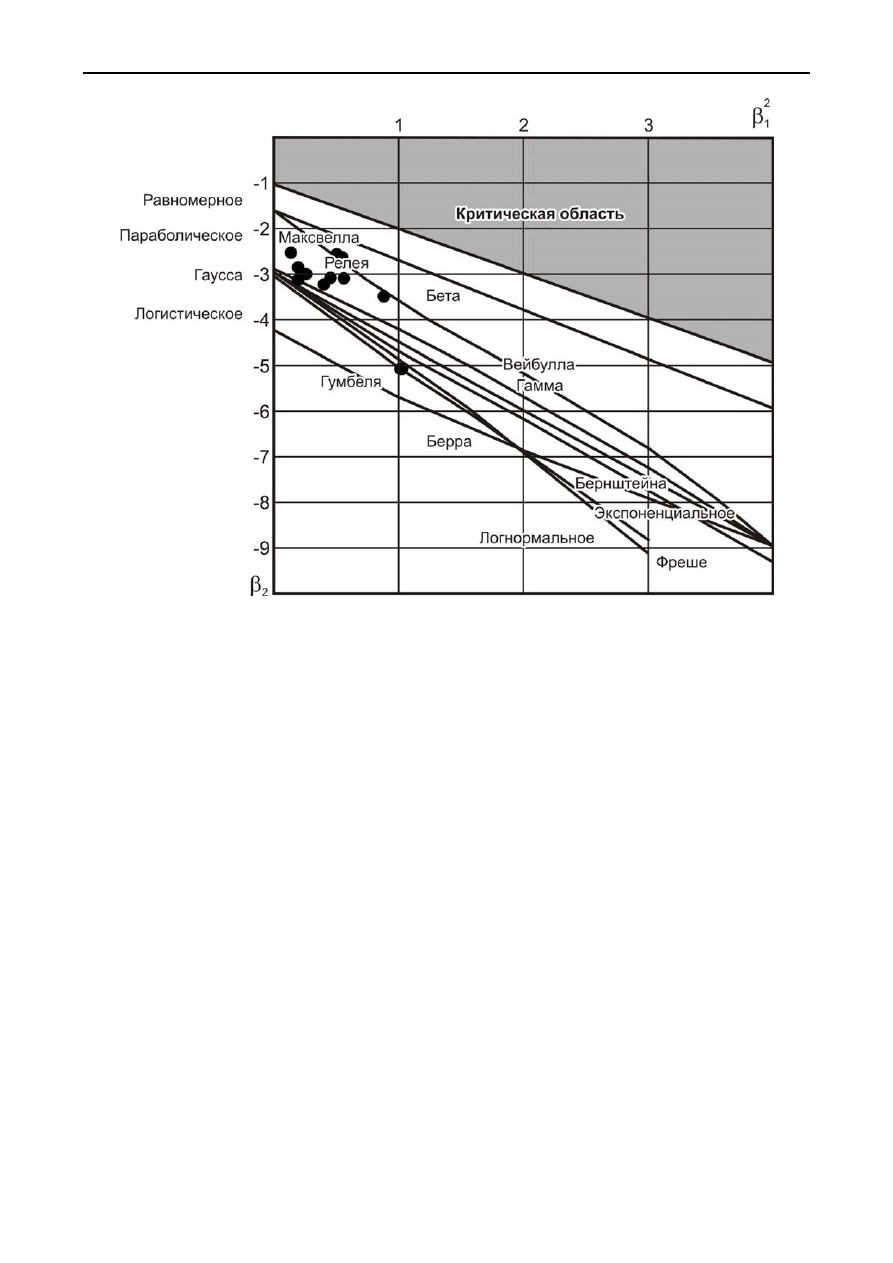
В
[
212]
подбор
распределений
по
экспериментальным
данным
рекоменду
-
ется
осуществлять
с
помощью
графика
Пирсона
,
на
котором
в
осях
координат
2
1
β
,
2
β
построены
кривые
,
соответствующие
различным
теоретическим
рас
-
пределениям
.
В
работе
[
181
]
этот
график
дополнен
точками
и
кривыми
,
пред
-
ставляющими
распределения
:
параболическое
,
логистическое
,
Берра
,
Максвел
-
ла
,
Релея
,
Гумбеля
,
Бернштейна
и
Фреше
.
Распределения
,
имеющие
только
два
параметра
(
положения
и
масштаба
),
изображаются
на
графике
точкой
.
К
ним
относятся
распределения
:
равномерное
,
параболическое
,
нормальное
,
Максвел
-
ла
,
Релея
,
логистическое
,
минимальных
и
максимальных
значений
Гумбеля
.
Кривые
с
тремя
параметрами
(
третий
–
параметр
формы
)
изображены
ли
-
ниями
( )
2
2
1
β
ϕ
β
=
.
К
ним
относятся
распределения
:
минимальных
и
макси
-
мальных
значений
Вейбулла
,
гамма
,
Бернштейна
,
логарифмически
нормальное
(
Гальтона
),
Берра
,
минимальных
и
максимальных
значений
Фреше
.
Бета
-
распределение
,
имеющее
два
параметра
формы
,
занимает
на
этом
графике
оп
-
ределенную
область
.
Точки
с
координатами
(
2
1
β
,
2
β
),
полученные
как
результат
обработки
ис
-
пытаний
образцов
,
нанесены
на
график
Пирсона
(
рис
. 5.4).
Р
АЗДЕЛ
5
104
Рис
. 5.4.
График
Пирсона
для
различных
распределений
случайных
величин
Видно
,
что
большинство
эмпирических
точек
группируются
в
некоторой
области
,
близко
расположенной
к
точке
,
соответствующей
нормальному
рас
-
пределению
(
для
нормального
распределения
2
1
β
=0,
2
β
=3).
На
этом
основании
можно
выдвинуть
гипотезу
о
распределении
прочности
образцов
на
одноосное
сжатие
по
нормальному
закону
.
При
этом
,
очевидно
,
что
кривая
Гаусса
не
вполне
отвечает
физической
природе
тех
величин
,
которые
по
своей
сути
не
могут
быть
отрицательными
.
В
[213]
отмечается
,
что
теоретически
хорошо
обоснованный
нормальный
закон
распределения
является
скорее
исключением
,
чем
правилом
,
которому
следуют
природные
явления
.
Исследуя
прочность
структурных
элементов
породного
массива
,
реальны
-
ми
«
представителями
»
которых
являются
образцы
,
изготовленные
из
отобран
-
ных
проб
,
следует
обратить
внимание
на
следующие
обстоятельства
.