ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1765
Скачиваний: 2
Р
АЗДЕЛ
7
170
к тому, что результаты моделирования
263
, полученные при использовании
алгоритма, построенного на основе этой модели, достаточно хорошо отражают
распределение напряжений в окрестности выработки, но дают существенно за-
ниженные значения перемещений, что не совпадает с данными натурных изме-
рений. В этой связи требуется уточнение описанной в
259
процедуры пошаго-
вого решения и учета в алгоритме численной реализации той части диаграммы
деформирования, которая отвечает объемным деформациям образца при испы-
таниях за пределом прочности и которая ответственна за перемещения в окре-
стности выработки.
Итак, любая произвольно выбранная точка в окрестности выработки нахо-
дится в условиях трехкомпонентного напряженного состояния, уровень которо-
го таков, что вокруг выработки образуется область горных пород с частично
разрушенными вследствие «жесткого» деформирования связями. Объемное на-
пряженное состояние можно заменить эквивалентным одноосным, используя
подходящий критерий прочности
73
. Выдвигается гипотеза соответствия: ха-
рактер изменения эквивалентных напряжений в окрестности выработки в точ-
ности совпадает с кривой разрушения породного образца в режиме заданных
деформаций.
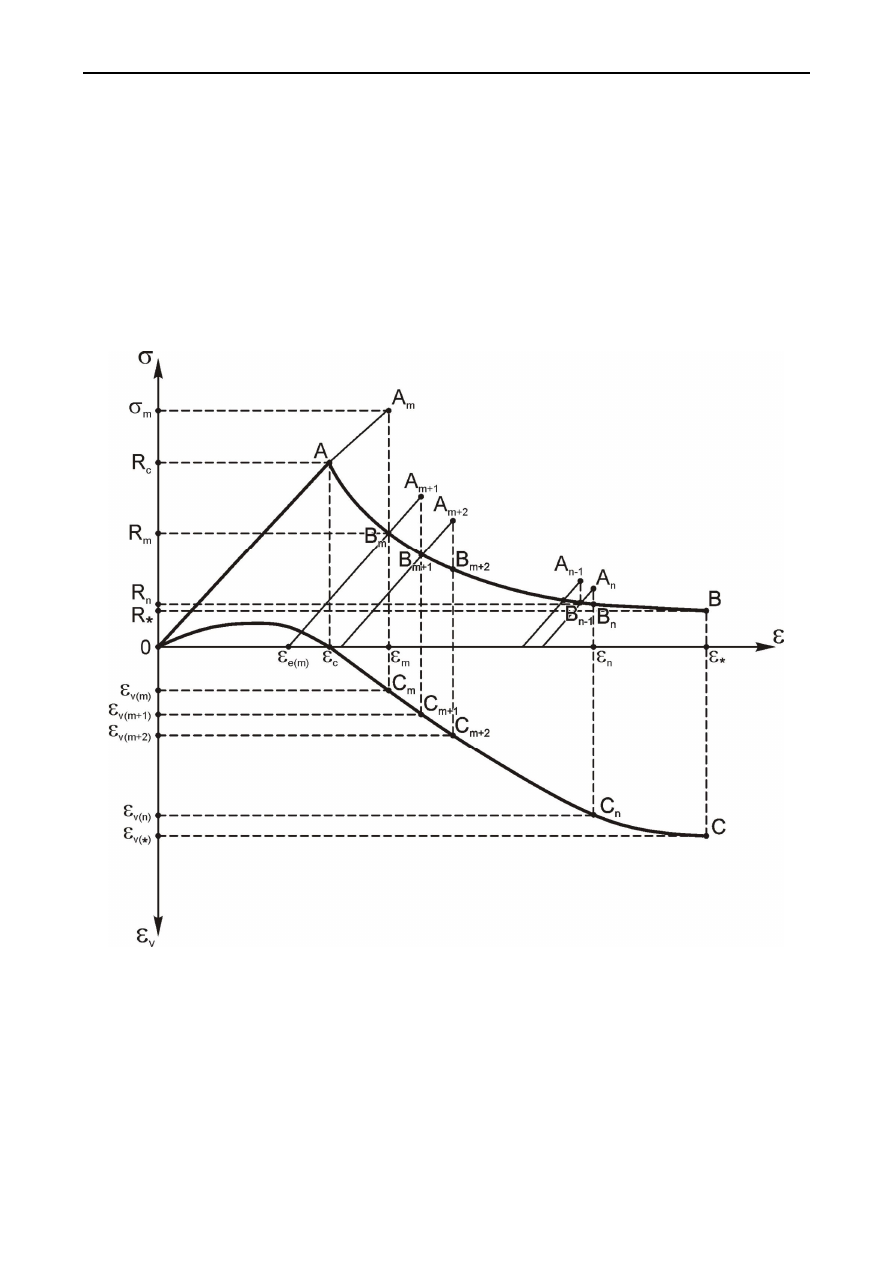
Рассмотрим идеализированную диаграмму деформирования, состоящую из
трех частей (рис. 7.4): линейного участка чисто упругой деформации
OA
, нис-
падающей ветви предельных напряженных состояний
AB
и ветви
OC
, описы-
вающей объемные деформации –
v
. Точка
A
соответствует предельным на-
пряжениям и деформациям упругости
0
,
,
v
c
c
R
, а точки
B
и
C
–
напряжениям и деформациям окончательного разрушения (
*
*
,
R
,
(*)
v
v
).
Пусть задано некоторое количество шагов
n
, за которое должна быть дос-
тигнута некоторая деформация
n
,
*
n
c
. Отметим, что в данной ситуа-
ции задание пути по деформациям является единственно возможным, посколь-
ку любому значению напряжения
, которое находится в пределах
*
R
c
R
,
Ч
ИСЛЕННЫЕ РЕШЕНИЯ УПРУГО
-
ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
171
соответствуют два значения деформации (на упругом и ниспадающем участ-
ках). Это согласуется с выдвинутой гипотезой, в соответствии с которой упруго
деформированная часть породного массива, размеры и жесткость которого
можно считать бесконечно большими, выполняет роль нагружающего устрой-
ства кинематического типа по отношению к зоне (области) неупругих дефор-
маций (ЗНД).
Рис. 7.4. К описанию модели пошагового решения, учитывающего объемные
деформации горной породы за пределом прочности
Пусть также ниспадающая ветвь диаграммы определена некоторым функ-
циональным соотношением [259]
Р
АЗДЕЛ
7
172
( )
0
,
0
0
;
>
=
⎟
⎠
⎞
⎜
⎝
⎛ −
−
=
ε
ε
σ
d
df
f
E
R
f
R
c
c
,
(7.58)
где
E
–
модуль
Юнга
.
Ниспадающая
ветвь
диаграммы
,
в
соответствии
с
предлагаемой
физиче
-
ской
моделью
,
представляет
собой
геометрическое
место
точек
предельных
со
-
стояний
,
эквивалентных
одноосному
нагружению
породного
образца
с
оста
-
точными
упругими
и
частично
разрушенными
структурными
связями
,
что
со
-
ответствует
наличию
в
произвольной
точке
i
B
ЗНД
упругой
и
диссипативной
энергии
.
В
частности
,
функция
f
может
являться
кусочно
-
линейной
аппрокси
-
мацией
результатов
испытаний
на
одноосное
сжатие
.
Предположим
,
что
в
пошаговом
процессе
чисто
упругого
деформирования
на
участке
OA
на
некотором
шаге
m
предельная
величина
напряжения
c
R
была
превышена
таким
образом
,
что
конечной
точкой
шага
является
некоторая
точка
(
)
m
m
m
A
σ
ε
,
.
В
соответствии
с
функциональной
зависимостью
(7.58)
может
быть
определена
точка
(
)
m
m
m
R
B
,
ε
,
лежащая
на
ниспадающей
ветви
AB
диаграммы
деформирования
.
Тогда
величины
m
ε
,
E
R
m
m
e
=
)
(
ε
,
)
(
)
(
m
e
m
m
d
ε
ε
ε
−
=
пред
-
ставляют
собой
соответственно
полную
,
упругую
и
диссипативную
(
остаточ
-
ную
)
деформации
в
точке
m
B
.
Объемную
деформацию
в
точке
m
B
определим
,
используя
кривую
объемных
деформаций
v
ε
.
Так
,
точке
m
B
поставлена
в
соот
-
ветствие
точка
m
C
,
лежащая
на
кривой
объемных
деформаций
,
и
соответст
-
вующее
ей
значение
)
(
m
v
ε
.
Таким
образом
,
используя
ниспадающую
кривую
диаграммы
деформиро
-
вания
,
мы
определяем
предельное
напряженное
состояние
в
точке
m
B
,
при
этом
нижняя
часть
диаграммы
позволяет
получить
объемные
деформации
и
,
при
из
-
вестном
из
экспериментов
соотношении
между
продольными
и
поперечными
составляющими
,
перемещения
в
заданной
точке
приконтурного
пространства
.
Введем
величину
m
m
m
R
σ
σ
−
=
)
(
0
,
которую
назовем
начальным
напряже
-
нием
для
шага
m
в
рассматриваемой
точке
разрыхленной
части
породного
мас
-
сива
.
Начальные
напряжения
будут
играть
существенную
роль
при
конечно
-
элементном
решении
граничной
задачи
.
Ч
ИСЛЕННЫЕ
РЕШЕНИЯ
УПРУГО
-
ПЛАСТИЧЕСКИХ
ЗАДАЧ
ПРИМЕНИТЕЛЬНО
К
УСТОЙЧИВОСТИ
ПОДЗЕМНЫХ
ВЫРАБОТОК
173
На
шаге
1
+
m
вновь
производится
чисто
упругое
решение
задачи
,
но
уже
исходя
из
точки
m
B
.
В
результате
достигается
точка
1
+
m
A
,
в
соответствии
с
уравнением
(7.58)
определяются
точки
1
+
m
B
,
1
+
m
C
(
см
.
рис
. 7.4)
и
аналогично
вышеописанному
–
величины
1
+
m
ε
,
)
1
(
+
m
v
ε
,
1
+
m
R
и
)
1
(
0
+
m
σ
(
на
рисунке
не
пока
-
заны
).
Затем
процесс
повторяется
до
тех
пор
,
пока
на
последнем
шаге
n
не
бу
-
дет
достигнута
конечная
деформация
n
ε
в
точке
(
)
n
n
n
R
B
,
ε
.
Таким
образом
,
на
протяжении
всего
процесса
решения
имеет
место
выход
на
ниспадающие
уча
-
стки
диаграммы
,
которые
являются
геометрическим
местом
точек
предельных
упругих
состояний
материала
[259].
Отметим
,
что
в
методе
упругих
решений
для
упрочняющихся
материалов
[262]
на
каждом
шаге
вместо
упругого
модуля
E
часто
используется
пластиче
-
ский
касательный
модуль
0
~
~
>
=
пл
пл
tg
d
d
E
ε
σ
в
текущей
точке
диаграммы
,
где
σ
~
является
интенсивностью
напряжений
,
а
пл
ε
~ –
интенсивностью
пластических
деформаций
.
Для
разупрочняющихся
материалов
,
одним
из
которых
является
разрыхленная
горная
порода
,
использование
касательного
модуля
не
является
желательным
,
поскольку
0
<
tg
E
.
Для
решения
краевой
задачи
метод
,
описанный
выше
,
следует
обобщить
на
случай
трехосного
напряженного
состояния
.
Здесь
нет
возможности
воспользо
-
ваться
,
например
,
гипотезой
единой
кривой
(
как
в
деформационной
теории
пла
-
стичности
)
или
гипотезой
,
что
касательный
модуль
tg
E
является
универсальной
функцией
интенсивности
пластических
деформаций
пл
ε
~ (
как
в
теории
течения
с
изотропным
упрочнением
).
Это
вызвано
тем
,
что
горные
породы
при
растяже
-
нии
и
сдвиге
ведут
себя
совершенно
иначе
,
чем
при
сжатии
.
В
частности
,
экс
-
периментально
установлено
,
что
для
многих
пород
предельное
напряжение
при
растяжении
c
р
R
R
1
,
0
≈
,
а
при
сдвиге
,
как
было
показано
в
разделе
3.1,
соответ
-
ствующее
предельное
напряжение
составляет
c
р
R
R
R
5
,
0
≈
τ
.
Рассмотрим
сначала
случай
сдвиговых
деформаций
.
Пусть
мы
имеем
неко
-
торую
точку
( )
σ
ε
,
D
,
полученную
из
эксперимента
на
одноосное
сжатие
(
при
Р
АЗДЕЛ
7
174
этом
мы
исходим
из
того
,
что
в
этой
точке
выполняется
равенство
(7.58)).
На
-
шей
задачей
является
поставить
ей
в
соответствие
другую
точку
–
( )
τ
γ
,
S
.
Тогда
всем
точкам
ниспадающей
ветви
диаграммы
одноосного
сжатия
будут
постав
-
лены
в
соответствие
точки
ниспадающей
ветви
диаграммы
сдвига
.
Одной
из
возможностей
является
использование
следующих
равенств
.
,
2
σ
τ
σ
σ
ε
γ
τ
τ
c
c
R
R
G
R
R
E
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
(7.59)
Эти
формулы
означают
,
что
для
диаграммы
«
γ
τ
~ »
модуль
сдвига
равен
G
,
предельное
напряжение
сдвига
равно
τ
R
.
В
первом
из
соотношений
(7.59)
из
полной
деформации
сжатия
вычитается
ее
упругая
составляющая
,
после
чего
добавляется
соответствующим
образом
масштабированная
упругая
деформация
сдвига
.
Множитель
2
присутствует
,
поскольку
деформация
сдвига
равна
удво
-
енной
сдвиговой
компоненте
тензора
деформаций
,
т
.
е
.
(
)
j
i
ij
ij
≠
=
ε
γ
2
в
об
-
щем
случае
.
Аналогично
можно
рассмотреть
и
построение
кривой
«
ε
σ
~
»,
где
3
33
22
11
σ
σ
σ
σ
+
+
=
,
3
33
22
11
ε
ε
ε
ε
+
+
=
есть
среднее
напряжение
и
средняя
де
-
формация
соответственно
.
В
упругой
области
ε
σ
K
=
,
где
K
–
модуль
Брид
-
жмена
.
Рассмотрим
сначала
случай
объемного
расширения
.
При
этом
следует
учесть
,
что
при
растяжении
,
как
уже
упоминалось
,
предельное
напряжение
c
р
R
R
<
.
Тогда
,
по
аналогии
с
выражениями
(7.59),
можно
записать
.
3
1
,
3
1
K
R
R
K
R
R
E
c
р
c
р
σ
σ
σ
σ
ε
ε
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
(7.60)