ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1763
Скачиваний: 2
Ч
ИСЛЕННЫЕ РЕШЕНИЯ УПРУГО
-
ПЛАСТИЧЕСКИХ ЗАДАЧ ПРИМЕНИТЕЛЬНО К УСТОЙЧИВОСТИ ПОДЗЕМНЫХ ВЫРАБОТОК
175
Обозначения компонент, входящих в соотношения (7.60), также аналогич-
ны введенным выше.
В
случае объемного сжатия
можно было бы записать формулы, схожие с
(7.60), но в которых отсутствуют коэффициенты
c
р
R
R
. Однако, более пред-
почтительно использовать приведенное в разделе 2.2 соотношение (2.2), полу-
ченное на основе анализа большого количества результатов экспериментов на
одноосное сжатие. Поскольку в данном случае речь идет об объемном сжатии,
то, в отличие от одноосного нагружения, данная формула может быть обобще-
на путем введения некоторых поправочных коэффициентов, полученных экс-
периментальным путем, и записана в виде
l
c
c
v
R
R
R
R
k
*
(*)
.
(7.61)
Здесь
(*)
v
– предельная величина объемного разыхления, определяемая из ис-
пытаний на одноосное сжатие,
1
k
,
1
l
– поправочные коэффициенты, опре-
деляемые экспериментально. Значения
1
k
,
1
l
соответствуют линейной за-
висимости между предельными эквивалентными напряжениями и величиной
объемной деформации.
Перейдем теперь к рассмотрению
общего напряженного состояния
. Для
сдвиговых компонент напряжений
)
(
,
j
i
ij
ij
можно использовать форму-
лы (7.59), где следует положить
3
,
2
,
1
,
;
,
j
i
j
i
ij
ij
. Что касается
нормальных напряжений и деформаций, то их можно разделить на гидростати-
ческую
,
и девиаторную
ij
ij
e
s
,
части:
,
,
ij
ij
ij
ij
ij
ij
e
s
(7.62)
где
ij
– символ Кронекера. Диаграмма для гидростатических составляющих
может быть построена по формулам (7.60), (7.61). Далее, поскольку именно де-
Р
АЗДЕЛ
7
176
виаторные
составляющие
нормальных
напряжений
ответственны
за
сдвиговые
деформации
,
можно
принять
,
что
для
них
кривая
деформирования
может
быть
определена
в
соответствии
с
диаграммой
испытаний
на
одноосное
сжатие
по
соотношениям
(7.59):
.
,
σ
σ
σ
ε
τ
τ
c
ij
c
ij
R
R
s
G
R
R
E
e
=
+
−
=
(
)
j
i
=
(7.63)
В
отличие
от
формулы
(7.59),
множитель
2
здесь
отсутствует
,
поскольку
речь
идет
о
девиаторных
составляющих
нормальных
деформаций
ij
e
,
но
не
о
деформации
сдвига
(
)
j
i
ij
ij
≠
=
ε
γ
2
.
Кроме
того
,
в
формуле
(7.61)
в
качестве
переменной
R
следует
использо
-
вать
эквивалентное
напряжение
,
определенное
в
соответствии
с
выражением
(3.19),
учитывающее
все
компоненты
тензора
напряжений
в
случае
трехосного
напряженного
состояния
.
7.3.
Конечноэлементная
реализация
алгоритма
решения
упругопла
-
стической
задачи
Рассматривается
достаточно
длинная
выработка
круговой
формы
,
находя
-
щаяся
в
толще
горных
пород
на
заданной
глубине
.
В
таких
случаях
в
сечениях
,
близких
к
середине
выработки
,
имеет
место
плоское
деформированное
состоя
-
ние
(
)
0
=
z
ε
,
поэтому
достаточно
рассмотреть
двумерную
краевую
задачу
.
Дальнейшее
описание
приведено
для
численного
решения
задачи
с
использова
-
нием
в
модели
8-
узловых
плоских
изопараметрических
элементов
с
девятью
точками
интегрирования
по
Гауссу
.
Достаточно
большая
область
,
которая
охва
-
тывает
выработку
,
разбивается
на
множество
таких
элементов
.
Соответствующим
образом
выбираются
закрепления
(
фиксируются
пере
-
мещения
в
характерных
точках
),
а
на
верхней
и
боковой
границах
области
(
рас
-
Ч
ИСЛЕННЫЕ
РЕШЕНИЯ
УПРУГО
-
ПЛАСТИЧЕСКИХ
ЗАДАЧ
ПРИМЕНИТЕЛЬНО
К
УСТОЙЧИВОСТИ
ПОДЗЕМНЫХ
ВЫРАБОТОК
177
сматривается
половина
выработки
в
силу
симметрии
расчетной
схемы
)
задается
равномерное
давление
,
которое
за
определенное
количество
шагов
n
возраста
-
ет
до
величины
,
соответствующей
заданной
глубине
.
Кроме
того
,
на
первом
шаге
учитывается
гравитационная
нагрузка
.
На
каждом
шаге
в
соответствии
с
приращением
внешнего
давления
в
узлах
конечно
-
элементного
разбиения
определяются
приращения
перемещений
,
а
в
точках
интегрирования
Гаусса
каждого
конечного
элемента
–
соответствующие
приращения
деформаций
и
напряжений
.
В
соответствии
с
найденными
прира
-
щениями
перемещений
рассчитываются
текущие
координаты
узлов
,
что
дает
картину
деформированной
области
.
Найденные
приращения
суммируются
с
перемещениями
,
напряжениями
и
деформациями
,
определенными
на
предыду
-
щем
шаге
.
Затем
нормальные
компоненты
напряжений
ij
σ
и
деформаций
ij
ε
разделяются
на
гидростатическую
и
девиаторную
составляющие
.
Для
каждой
из
них
,
так
же
как
и
для
сдвиговых
компонент
,
определяется
,
не
превышено
ли
предельное
значение
по
напряжениям
(
c
R
,
р
R
или
τ
R
).
Если
это
имеет
место
,
то
считается
,
что
данная
точка
интегрирования
Гаусса
претерпела
преобразование
(
т
.
е
.
вошла
в
стадию
неупругого
деформирования
),
и
для
нее
в
дальнейшем
реализуется
алгоритм
,
описанный
выше
–
соответствующая
компонента
(
гид
-
ростатическая
,
девиаторная
или
сдвиговая
) «
усекается
»
таким
образом
,
чтобы
выйти
на
соответствующую
кривую
деформирования
,
построенную
по
форму
-
лам
(7.59), (7.60)
или
(7.63).
После
этого
находятся
«
истинные
»
значения
ком
-
понент
напряжений
ij
R
и
значения
«
начальных
напряжений
»
ij
ij
ij
R
σ
σ
−
=
0
(
только
для
тех
компонент
тензора
напряжений
,
для
которых
предельное
значе
-
ние
было
превышено
).
Эти
«
начальные
напряжения
»
на
следующем
шаге
ре
-
шения
задачи
включаются
в
вектор
узловых
нагрузок
,
тем
самым
учитывая
,
что
в
данной
точке
интегрирования
Гаусса
происходит
не
чисто
упругое
деформи
-
рование
,
а
деформирование
вдоль
ниспадающего
участка
диаграммы
.
На
сле
-
дующем
шаге
описанная
процедура
повторяется
,
с
той
разницей
,
что
для
тех
точек
,
которые
уже
претерпели
преобразование
,
предельным
значением
будет
Р
АЗДЕЛ
7
178
соответствующая
компонента
ij
R
,
найденная
на
предыдущем
шаге
.
При
этом
в
формуле
(7.63)
следует
использовать
именно
компоненты
тензора
ij
R
(
точнее
,
его
главные
значения
).
Если
все
точки
интегрирования
Гаусса
данного
конечного
элемента
пере
-
шли
в
неупругое
состояние
,
то
считается
,
что
весь
элемент
перешел
в
неупру
-
гое
состояние
.
Набор
таких
элементов
представляет
собой
ЗНД
,
окружающую
выработку
.
По
мере
роста
внешней
нагрузки
эта
зона
расширяется
.
Несколько
иначе
реализуется
алгоритм
в
тех
точках
Гаусса
,
в
которых
на
-
блюдается
гидростатическое
сжатие
(
)
0
<
σ
.
Чтобы
избежать
накопления
оши
-
бок
при
пошаговом
решении
,
на
всех
шагах
,
кроме
предпоследнего
(
)
1
−
n
,
по
-
лагается
,
что
гидростатическая
деформация
сжатия
0
=
ε
(
что
верно
для
всех
точек
,
не
входящих
в
ЗНД
).
На
(
)
1
−
n
-
м
шаге
напряжения
σ
в
зоне
неупругих
деформаций
не
«
усекаются
»,
и
,
следовательно
,
начальные
нормальные
напря
-
жения
ij
0
σ
не
определяются
.
Вместо
этого
принято
,
что
на
этом
(
и
только
на
этом
)
шаге
определены
начальные
деформации
ij
0
ε
,
в
которых
гидростатиче
-
ская
составляющая
равна
значению
,
определяемому
формулой
(7.61).
На
по
-
следнем
шаге
n
эти
начальные
деформации
включаются
в
вектор
нагрузок
гло
-
бальной
системы
уравнений
относительно
приращений
узловых
перемещений
.
После
их
определения
,
нахождения
полных
перемещений
i
u
,
напряжений
ij
σ
,
деформаций
ij
ε
и
«
усечения
»
соответствующих
компонент
напряжений
в
ЗНД
до
величины
ij
R
решение
задачи
считается
законченным
.
Адекватность
численного
алгоритма
оценивается
степенью
соответствия
полученного
численного
решения
известным
строгим
аналитическим
решениям
аналогичной
задачи
.
В
качестве
тестовой
задачи
использовалось
аналитическое
решение
,
приведенное
в
параграфе
7.1.
С
использованием
алгоритма
,
описанного
выше
,
определялось
напряжен
-
но
-
деформированное
состояние
однородного
изотропного
породного
массива
,
Ч
ИСЛЕННЫЕ
РЕШЕНИЯ
УПРУГО
-
ПЛАСТИЧЕСКИХ
ЗАДАЧ
ПРИМЕНИТЕЛЬНО
К
УСТОЙЧИВОСТИ
ПОДЗЕМНЫХ
ВЫРАБОТОК
179
ослабленного
одиночной
выработкой
кругового
очертания
и
подверженного
гидростатическому
сжатию
.
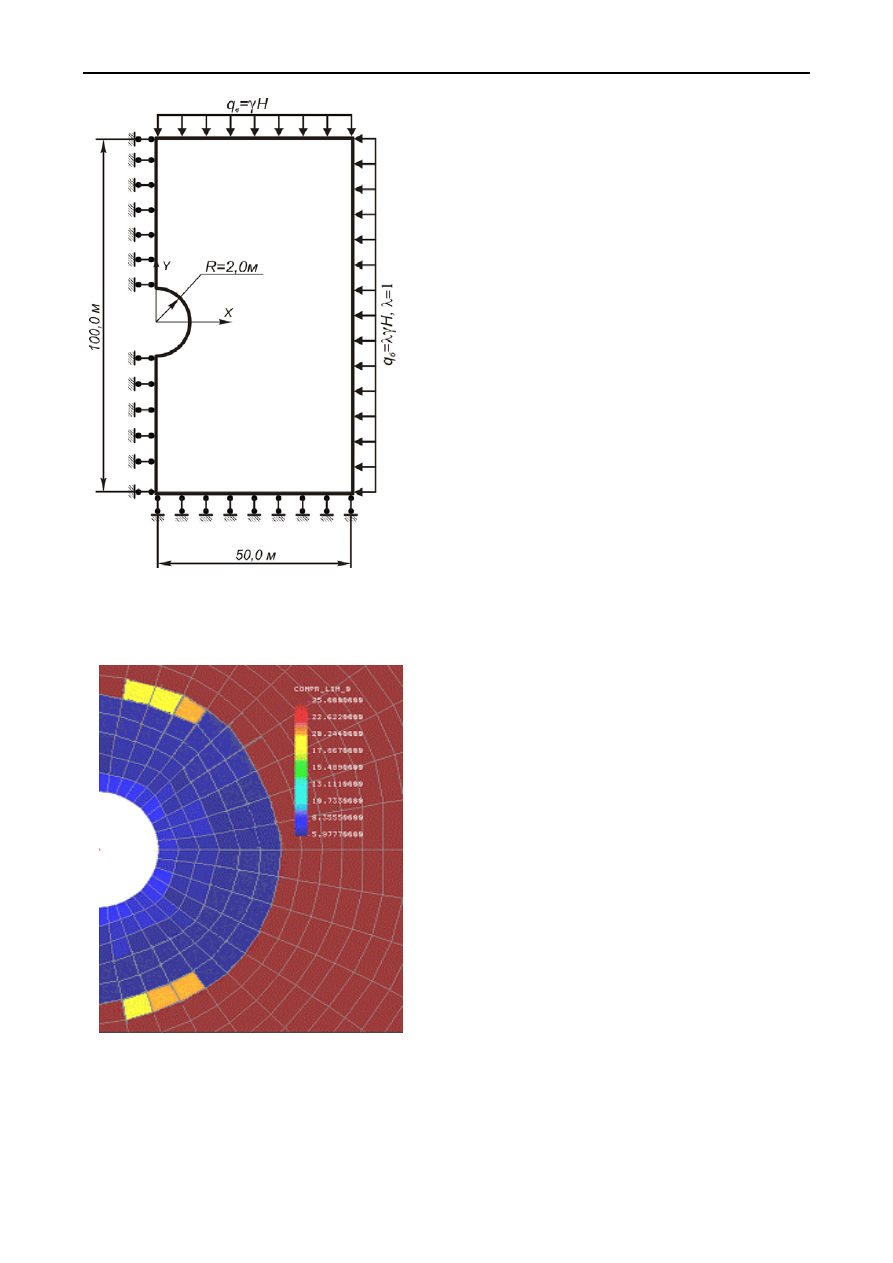
Расчетная
схема
представлена
на
рисунке
7.5.
Сравнение
с
аналитическим
реше
-
нием
проводилось
по
параметрам
L
r
(
от
-
носительный
радиус
ЗНД
)
и
0
u
(
величи
-
на
смещений
на
контуре
выработки
).
Аппроксимация
исследуемой
об
-
ласти
массива
осуществлялась
четырех
-
узловыми
конечными
элементами
,
ис
-
ходные
данные
к
численному
решению
принимались
такими
же
,
как
и
в
анали
-
тическом
решении
(
см
.
параграф
7.1).
Конфигурация
зоны
неупругих
де
-
формаций
,
полученная
в
ходе
упруго
-
пластического
численного
решения
тес
-
товой
задачи
,
представлена
на
рисун
-
ке
7.6.
Совокупность
элементов
,
окру
-
жающих
выработку
и
имеющих
различ
-
ные
оттенки
окраски
,
и
есть
искомая
зо
-
на
неупругих
деформаций
.
Различие
в
оттенках
обусловлено
различной
степе
-
нью
разрушения
материала
в
пределах
этой
зоны
.
Величины
сравниваемых
парамет
-
ров
,
полученные
из
аналитического
и
численного
решения
,
представлены
в
таблице
7.1.
Как
видно
из
таблицы
,
на
-
Рис
. 7.5.
Расчетная
схема
тестовой
задачи
Рис
. 7.6.
Конфигурация
зоны
неупругих
деформаций
(
тестовая
задача
)