ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 364
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
МОДУЛЬ 1. Предметная область метрологии
МОДУЛЬ 2. ШКАЛЫ И ПРИМЕНЕНИЕ ИХ В МЕТРОЛОГИИ
МОДУЛЬ 3. Физические величины, системы единиц физических величин
МОДУЛЬ 4. КЛАССИФИКАЦИЯ ИЗМЕРЕНИЙ. ПОНЯТИЕ О КАЧЕСТВЕ ИЗМЕРЕНИЙ
МОДУЛЬ 5. КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
МОДУЛЬ 6. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ
МОДУЛЬ 7. АНАЛИЗ ТОЧЕЧНЫХ ДИАГРАММ
МОДУЛЬ 8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА И ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
МОДУЛЬ 13. СРЕДСТВА ИЗМЕРЕНИЙ. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
МОДУЛЬ 14. ЭТАЛОНЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН И ПЕРЕДАЧА ЕДИНИЦ ОТ ЭТАЛОНОВ
средства измерений называлась составляющая погрешности, дополнительная к статической, и возникающая при измерении в динамическом режиме. В соответствии с определением
дин = д.р– ст.р ,
где дин – динамическая погрешность средства измерения;
д.р – погрешность средства измерения при использовании его в динамическом режиме;
ст.р – статическая погрешность средства измерения (погрешность при использовании средства измерений в статическом режиме).
Динамический режим измерений встречается не только при измерении изменяющейся величины, но и при измерении величины постоянной. И в том и в другом случаях (рисунок 5.5) возможна слишком высокая скорость «подачи информации» на средство измерений VQ (скорость изменения сигнала измерительной информации на входе средства измерений), которая оказывается соизмерима со скоростью преобразования измерительной информации VQX и/или даже выше ее.

Например, в контрольно-сортировочных автоматах для измерения диаметров тел качения подшипников измеряется постоянная физическая величина – длина. Но из-за необходимости обеспечить высокую производительность автомата скорость изменения входного сигнала измерительной информации может оказаться выше скорости преобразования измерительной информации средством измерения. В таком случае из-за «запаздывания» с преобразованием сигнала возникают динамические погрешности (рисунок 5.6).
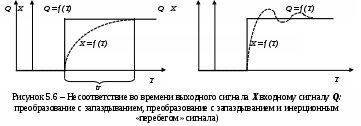
Поскольку речь идет не столько о средствах измерений, сколько об их работе в специфическим режиме, динамическую погрешность не следует считать инструментальной. Эту погрешность нужно рассматривать более широко – как составляющую итоговой (интегральной) погрешности, обусловленную динамическим режимом измерений.
Логически обоснованной представляется следующая укрупненная классификация погрешностей измерений по степени полноты информации об их характере и значениях:
К определенным можно отнести любые известные по числовому значению и знаку погрешности.
Известными могут стать, например те составляющие погрешности измерений, которые имеют достаточно жесткую функциональную связь с вызывающими их аргументами. Такие погрешности по сути совпадают с систематическими и принципиально могут быть выявлены и исключены из результатов измерений, их значения можно прогнозировать. Определенной можно считать также любуюпогрешность (в том числе и уже зафиксированную случайную или даже грубую), числовое значение и знак которой получены экспериментальными методами.
Определенные погрешности при достаточной полноте информации могут быть исключены из результатов измерений. Теоретическая определенность систематических погрешностей делает возможным исключение этих погрешностей до измерений, в процессе измерений, а также при математической обработке результатов измерительного эксперимента после выполнения измерений.
В тех случаях, когда погрешность становится определенной, в результат измерений может быть внесена поправка – значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Знак поправки противоположен знаку погрешности. Иногда поправки вносят, используя поправочный множитель (например, в случаях, когда систематическая погрешность пропорциональна значению величины)
Исключение систематических погрешностей измерения не только из отдельных результатов измерений, но из целых серий, полученных при многократных измерениях одной и той же физической величины, в метрологии принято называть «исправлением результатов», а полученные при этом результаты – исправленными. Статистическая обработка массивов результатов измерений, образующих серии, недопустима без предварительного «исправления результатов», т.е. без исключения по крайней мере, переменных систематических составляющих погрешностей.
К неопределенным погрешностям следует отнести невыявленные систематические погрешности, а также погрешности случайные (собственно случайные) и грубые, значения которых не были определены экспериментально. При исключении определенных погрешностей абсолютная точность невозможна, поэтому приходится относить к неопределенным неисключенные остатки погрешностей.
Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости. (Иногда этот вид погрешности называют неисключенный остаток систематической погрешности).
Наиболее интересна здесь возможность анализа ансамбля неисключенных остатков систематических погрешностей как массива случайно распределенных величин. Парадоксальность ситуации заключается в том, что массив случайно распределенных величин состоит из погрешностей, каждая из которых является систематической. Однако, для того, чтобы получить такой ансамбль, в ряде случаев приходится прибегать к его специальной организации. Такой прием называют рандомизацией систематических погрешностей. Иногда рандомизация получается самопроизвольно, но для того, чтобы использовать для оценки таких погрешностей математический аппарат теории вероятностей и математической статистики, необходимо убедиться, что мы в действительности имеем дело со случайным распределением исследуемых величин.
Как и все другие погрешности, неопределенные систематические погрешности могут быть либо значимыми, либо пренебрежимо малыми. К значимым неопределенным систематическим погрешностям относятся те невыявленные систематические погрешности и неисключенные остатки систематических погрешностей, которые соизмеримы со случайными составляющими погрешности измерений.
Невыявленные систематические погрешности, существенно превосходящие случайные составляющие, могут возникать из-за ошибок, допущенных разработчиками методики измерений вследствие недостаточной метрологической квалификации, либо из-за низкой квалификации операторов, стабильно повторяющих неправильные операции при выполнении измерительной процедуры. Причинами таких погрешностей могут быть также значительные отличия условий измерений от нормальных, не замеченные из-за невнимательного отношения оператора. Невыявленные систематические погрешности, превосходящие случайные составляющие, могут привести к существенному искажению результатов измерений, что особенно опасно при выполнении прецизионных измерений со сравнительно малыми случайными составляющими погрешностей. В грамотно организованных измерениях значимые невыявленные систематические погрешности не имеют права на существование, они подлежат обязательному выявлению
(переводу в определенные погрешности) и оценке либо исключению.
Неисключенные остатки систематических погрешностей имеют место при любом, даже самом тщательном выявлении и исключении систематических составляющих. Поскольку далеко не всегда удается выявить вид зависимости аргумент-погрешность, а в ряде случаев неизвестными остаются и сами значения аргументов, в результатах измерений всегда присутствуют неисключенные систематические погрешности, которые в соответствии с предлагаемой классификацией относятся к погрешностям неопределенным.
В принципе эти погрешности могут быть выявлены и исключены (как систематические), однако иногда они остаются невыявленными из-за сложности технического решения такой задачи (малые значения погрешностей, сложные закономерности их изменения и ограниченность информации). В подобных случаях необходимо оценивать предельные значения этих погрешностей или их порядок. Если измерения характеризуются наличием нескольких неисключенных остатков систематических погрешностей, для расчета результирующего («суммарного») значения неисключенных систематических погрешностей применяют аппарат теории вероятностей и математической статистики, в силу сходства механизмов формирования ансамбля этих погрешностей и случайных величин (допущение о самопроизвольной рандомизации).
Применение этого математического аппарата тем более оправдано в случаях, когда систематическая погрешность отдельной реализации является случайной величиной в ансамбле однородных событий. Например, систематическая погрешность конкретной меры массы (гири) является случайной для партии мер одного номинала и одного класса точности. Предельное значение (граница) такой погрешности может быть определена как граница поля допуска меры.
Проведенный анализ позволяет оценить правомочность применения стохастического подхода к таким детерминированным величинам, как неисключенные систематические погрешности. Статистическая обработка ансамбля неисключенных систематических составляющих приводит к появлению таких парадоксальных оценок, как значение среднего квадратического отклонения систематической составляющей погрешности и связанные с ним предельные значения или доверительные границы неисключенных остатков систематической погрешности с указанием доверительной вероятности, а также качественные оценки (принятая аппроксимация) закона распределения. Методы выявления и оценки таких погрешностей описаны в соответствующем модуле. Если полученные оценки значений неисключенных систематических погрешностей соизмеримы со случайными составляющими, расчет «суммарного» значения неисключенных остатков систематических погрешностей и учет их совместного со случайными составляющими влияния на результаты измерений должен осуществляться с применением специального аппарата математической обработки, который приведен в ГОСТ 8.207.
Неисключенными систематическими составляющими, значения которых существенно меньше случайных погрешностей (s < 0,8), пренебрегают. Такие погрешности относят к пренебрежимо малым составляющим погрешности измерения (правомерно не исключенным остаткам систематических погрешностей). Принято считать, что их наличие не вносит существенных искажений в результаты статистической обработки экспериментальных данных. В подобных случаях результаты измерений, содержащие наряду со случайными составляющими неисключенные остатки систематических погрешностей, часто подвергают обычной статистической обработке, не отделяя погрешности друг от друга.
Общеприняты и практически непротиворечивы классификации погрешностей измерений по используемым формам выражения (рисунок 5.7). Фактически это классификация не самих погрешностей измерений, а именно форм их выражения.
Абсолютные погрешности выражают в единицах измеряемой величины, а относительные, которые представляют собой отношение абсолютной погрешности к значению измеряемой величины, могут быть рассчитаны в неименованных относительных единицах (или в именованных относительных единицах, например в процентах или в промилле). Формальное выражение относительной погрешности (отн) может быть представлено в виде:
отн = /Q,
а при использовании именованной относительной погрешности, выраженной в процентах
отн = (/Q) 100 %.
где – абсолютная погрешность измерения;
Q – истинное значение физической величины.

Либо, принимая во внимание незначительное для данного выражения различие между истинным значением физической величины Q и результатом ее измерения X, можно записать
отн/X,
а также
отн (/X) 100 %.
Для характеристикисредств измерений иногда используют такой специфический класс относительных погрешностей, как приведенные погрешности средств измерений (прив), то есть отношение абсолютной погрешности к некоторой нормирующей величине (Qнорм)
прив = /Qнорм,
В качестве нормирующей величины могут использоваться верхний предел измерений, либо больший из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений, а верхний и нижний пределы не одинаковы по модулю, и другие величины, оговоренные ГОСТ 8.401.
дин = д.р– ст.р ,
где дин – динамическая погрешность средства измерения;
д.р – погрешность средства измерения при использовании его в динамическом режиме;
ст.р – статическая погрешность средства измерения (погрешность при использовании средства измерений в статическом режиме).
Динамический режим измерений встречается не только при измерении изменяющейся величины, но и при измерении величины постоянной. И в том и в другом случаях (рисунок 5.5) возможна слишком высокая скорость «подачи информации» на средство измерений VQ (скорость изменения сигнала измерительной информации на входе средства измерений), которая оказывается соизмерима со скоростью преобразования измерительной информации VQX и/или даже выше ее.

Например, в контрольно-сортировочных автоматах для измерения диаметров тел качения подшипников измеряется постоянная физическая величина – длина. Но из-за необходимости обеспечить высокую производительность автомата скорость изменения входного сигнала измерительной информации может оказаться выше скорости преобразования измерительной информации средством измерения. В таком случае из-за «запаздывания» с преобразованием сигнала возникают динамические погрешности (рисунок 5.6).

Поскольку речь идет не столько о средствах измерений, сколько об их работе в специфическим режиме, динамическую погрешность не следует считать инструментальной. Эту погрешность нужно рассматривать более широко – как составляющую итоговой (интегральной) погрешности, обусловленную динамическим режимом измерений.
Логически обоснованной представляется следующая укрупненная классификация погрешностей измерений по степени полноты информации об их характере и значениях:
-
определенные погрешности, -
неопределенные погрешности.
К определенным можно отнести любые известные по числовому значению и знаку погрешности.
Известными могут стать, например те составляющие погрешности измерений, которые имеют достаточно жесткую функциональную связь с вызывающими их аргументами. Такие погрешности по сути совпадают с систематическими и принципиально могут быть выявлены и исключены из результатов измерений, их значения можно прогнозировать. Определенной можно считать также любуюпогрешность (в том числе и уже зафиксированную случайную или даже грубую), числовое значение и знак которой получены экспериментальными методами.
Определенные погрешности при достаточной полноте информации могут быть исключены из результатов измерений. Теоретическая определенность систематических погрешностей делает возможным исключение этих погрешностей до измерений, в процессе измерений, а также при математической обработке результатов измерительного эксперимента после выполнения измерений.
В тех случаях, когда погрешность становится определенной, в результат измерений может быть внесена поправка – значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Знак поправки противоположен знаку погрешности. Иногда поправки вносят, используя поправочный множитель (например, в случаях, когда систематическая погрешность пропорциональна значению величины)
Исключение систематических погрешностей измерения не только из отдельных результатов измерений, но из целых серий, полученных при многократных измерениях одной и той же физической величины, в метрологии принято называть «исправлением результатов», а полученные при этом результаты – исправленными. Статистическая обработка массивов результатов измерений, образующих серии, недопустима без предварительного «исправления результатов», т.е. без исключения по крайней мере, переменных систематических составляющих погрешностей.
К неопределенным погрешностям следует отнести невыявленные систематические погрешности, а также погрешности случайные (собственно случайные) и грубые, значения которых не были определены экспериментально. При исключении определенных погрешностей абсолютная точность невозможна, поэтому приходится относить к неопределенным неисключенные остатки погрешностей.
Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости. (Иногда этот вид погрешности называют неисключенный остаток систематической погрешности).
Наиболее интересна здесь возможность анализа ансамбля неисключенных остатков систематических погрешностей как массива случайно распределенных величин. Парадоксальность ситуации заключается в том, что массив случайно распределенных величин состоит из погрешностей, каждая из которых является систематической. Однако, для того, чтобы получить такой ансамбль, в ряде случаев приходится прибегать к его специальной организации. Такой прием называют рандомизацией систематических погрешностей. Иногда рандомизация получается самопроизвольно, но для того, чтобы использовать для оценки таких погрешностей математический аппарат теории вероятностей и математической статистики, необходимо убедиться, что мы в действительности имеем дело со случайным распределением исследуемых величин.
Как и все другие погрешности, неопределенные систематические погрешности могут быть либо значимыми, либо пренебрежимо малыми. К значимым неопределенным систематическим погрешностям относятся те невыявленные систематические погрешности и неисключенные остатки систематических погрешностей, которые соизмеримы со случайными составляющими погрешности измерений.
Невыявленные систематические погрешности, существенно превосходящие случайные составляющие, могут возникать из-за ошибок, допущенных разработчиками методики измерений вследствие недостаточной метрологической квалификации, либо из-за низкой квалификации операторов, стабильно повторяющих неправильные операции при выполнении измерительной процедуры. Причинами таких погрешностей могут быть также значительные отличия условий измерений от нормальных, не замеченные из-за невнимательного отношения оператора. Невыявленные систематические погрешности, превосходящие случайные составляющие, могут привести к существенному искажению результатов измерений, что особенно опасно при выполнении прецизионных измерений со сравнительно малыми случайными составляющими погрешностей. В грамотно организованных измерениях значимые невыявленные систематические погрешности не имеют права на существование, они подлежат обязательному выявлению
(переводу в определенные погрешности) и оценке либо исключению.
Неисключенные остатки систематических погрешностей имеют место при любом, даже самом тщательном выявлении и исключении систематических составляющих. Поскольку далеко не всегда удается выявить вид зависимости аргумент-погрешность, а в ряде случаев неизвестными остаются и сами значения аргументов, в результатах измерений всегда присутствуют неисключенные систематические погрешности, которые в соответствии с предлагаемой классификацией относятся к погрешностям неопределенным.
В принципе эти погрешности могут быть выявлены и исключены (как систематические), однако иногда они остаются невыявленными из-за сложности технического решения такой задачи (малые значения погрешностей, сложные закономерности их изменения и ограниченность информации). В подобных случаях необходимо оценивать предельные значения этих погрешностей или их порядок. Если измерения характеризуются наличием нескольких неисключенных остатков систематических погрешностей, для расчета результирующего («суммарного») значения неисключенных систематических погрешностей применяют аппарат теории вероятностей и математической статистики, в силу сходства механизмов формирования ансамбля этих погрешностей и случайных величин (допущение о самопроизвольной рандомизации).
Применение этого математического аппарата тем более оправдано в случаях, когда систематическая погрешность отдельной реализации является случайной величиной в ансамбле однородных событий. Например, систематическая погрешность конкретной меры массы (гири) является случайной для партии мер одного номинала и одного класса точности. Предельное значение (граница) такой погрешности может быть определена как граница поля допуска меры.
Проведенный анализ позволяет оценить правомочность применения стохастического подхода к таким детерминированным величинам, как неисключенные систематические погрешности. Статистическая обработка ансамбля неисключенных систематических составляющих приводит к появлению таких парадоксальных оценок, как значение среднего квадратического отклонения систематической составляющей погрешности и связанные с ним предельные значения или доверительные границы неисключенных остатков систематической погрешности с указанием доверительной вероятности, а также качественные оценки (принятая аппроксимация) закона распределения. Методы выявления и оценки таких погрешностей описаны в соответствующем модуле. Если полученные оценки значений неисключенных систематических погрешностей соизмеримы со случайными составляющими, расчет «суммарного» значения неисключенных остатков систематических погрешностей и учет их совместного со случайными составляющими влияния на результаты измерений должен осуществляться с применением специального аппарата математической обработки, который приведен в ГОСТ 8.207.
Неисключенными систематическими составляющими, значения которых существенно меньше случайных погрешностей (s < 0,8), пренебрегают. Такие погрешности относят к пренебрежимо малым составляющим погрешности измерения (правомерно не исключенным остаткам систематических погрешностей). Принято считать, что их наличие не вносит существенных искажений в результаты статистической обработки экспериментальных данных. В подобных случаях результаты измерений, содержащие наряду со случайными составляющими неисключенные остатки систематических погрешностей, часто подвергают обычной статистической обработке, не отделяя погрешности друг от друга.
Общеприняты и практически непротиворечивы классификации погрешностей измерений по используемым формам выражения (рисунок 5.7). Фактически это классификация не самих погрешностей измерений, а именно форм их выражения.
Абсолютные погрешности выражают в единицах измеряемой величины, а относительные, которые представляют собой отношение абсолютной погрешности к значению измеряемой величины, могут быть рассчитаны в неименованных относительных единицах (или в именованных относительных единицах, например в процентах или в промилле). Формальное выражение относительной погрешности (отн) может быть представлено в виде:
отн = /Q,
а при использовании именованной относительной погрешности, выраженной в процентах
отн = (/Q) 100 %.
где – абсолютная погрешность измерения;
Q – истинное значение физической величины.

Либо, принимая во внимание незначительное для данного выражения различие между истинным значением физической величины Q и результатом ее измерения X, можно записать
отн/X,
а также
отн (/X) 100 %.
Для характеристикисредств измерений иногда используют такой специфический класс относительных погрешностей, как приведенные погрешности средств измерений (прив), то есть отношение абсолютной погрешности к некоторой нормирующей величине (Qнорм)
прив = /Qнорм,
В качестве нормирующей величины могут использоваться верхний предел измерений, либо больший из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений, а верхний и нижний пределы не одинаковы по модулю, и другие величины, оговоренные ГОСТ 8.401.