Файл: Лекции по теоретической метрологии.doc

Формы оценок погрешностей, используемые в метрологии и в технических измерениях, весьма разнообразны. Они включают качественные характеристики и количественные оценки погрешностей измерений.

Качественные характеристики погрешностей в простейшем случае ограничиваются указанием их детерминированного или стохастического характера. Для систематических погрешностей дополнительно может быть указан характер зависимости (постоянная, прогрессирующая, периодическая), а при более полной информации – функция, описывающая изменение погрешности.

Для случайных погрешностей качественной характеристикой может быть аппроксимация функции плотностей распределения вероятностей. В метрологии приняты и наиболее часто применяются для аппроксимации нормальное распределение (распределение Гаусса), равновероятное, трапециевидное и распределение Релея. При необходимости используют и другие аппроксимации.

Случайная составляющая погрешности вызывает рассеяние результатов измерений, которое обычно обусловлено проявлением множества случайных причин и носит вероятностный характер. Рассеяние результатов в ряду измерений – несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей. Количественными оценками рассеяния результатов в ряду измерений могут быть:

• 
  размах результатов,
  
• 
  средняя арифметическая погрешность (по модулю),
  
• 
  средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение),
  
• 
  доверительные границы погрешности (доверительная граница или доверительная погрешность).
  

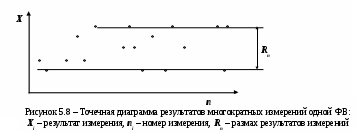
Размах результатов измерений (размах) – оценка Rn рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из п измерений). Размах результатов измерений Rn (рисунок 5.8) определяют из зависимости

R_n = X_max – X_min,

где X_maxи X_min – наибольшее и наименьшее значения результатов измерений в серии.

Размах отклонений R_e от среднего или произвольно выбранного значения, который равен размаху результатов измерений определяют из зависимости

---

R_e = e_max – e_min,

гдеe_maxи e_min – наибольшее и наименьшее отклонения результатов от некоторого фиксированного значения.

Более строгими в математическом смысле оценками погрешностей можно считать среднее арифметическое значение погрешности в серии результатов, значение средней квадратической погрешности (среднее квадратическое отклонение результата измерения от фиксированного значения точечной оценки), границы погрешности.




Средняя квадратическая погрешность результатов единичных измерений в ряду измерений(средняя квадратическая погрешность измерений; средняя квадратическая погрешность; СКП) – оценка рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения. В метрологической практике широко распространен термин среднее квадратическое отклонение (СКО) единичных результатов в ряду измерений от их среднего арифметического значения. Это отклонение иногда называют стандартной погрешностью измерений. Если в результаты измерений введены поправки для устранения систематических погрешностей, то отклонения от среднего арифметического значения можно рассматривать как случайные погрешности. В РМГ 29 – 99 предлагается для упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», применять термин «средняя квадратическая погрешность». При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО представляют собой одну и ту же оценку рассеяния результатов единичных измерений.

Границы погрешности могут быть определены как предельные значения или как доверительные границы с указанием вероятности попадания погрешности в указанный интервал. В качестве предельных значений или границ могут рассматриваться нижняя и верхняя границы (н и в либо – и +), значение модуля погрешности  (в случае если – = +) или значение модуля погрешности, равное большему из абсолютных значений – и +.

Доверительные границы погрешности результата измерений(доверительные границы погрешности; доверительные границы) – наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

---

Доверительные границы результата измерений при симметричном распределении вычисляются как , , где , – средние квадратические погрешности, соответственно, единичного и среднего арифметического результатов измерений; t – коэффициент, зависящий от доверительной вероятности Р и числа измерений п. При симметричных границах термин может применяться в единственном числе – доверительная граница. Иногда вместо термина доверительная границаприменяют термин доверительная погрешностьили погрешность при данной доверительной вероятности.

Термин средняя квадратическая погрешность результата измерений среднего арифметического (средняя квадратическая погрешность среднего арифметического; средняя квадратическая погрешность; СКП) введен вместо ранее применявшегося термина среднее квадратическое отклонение результата измерений. Значение этой оценки погрешности рассчитывается как СКО случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений по формуле



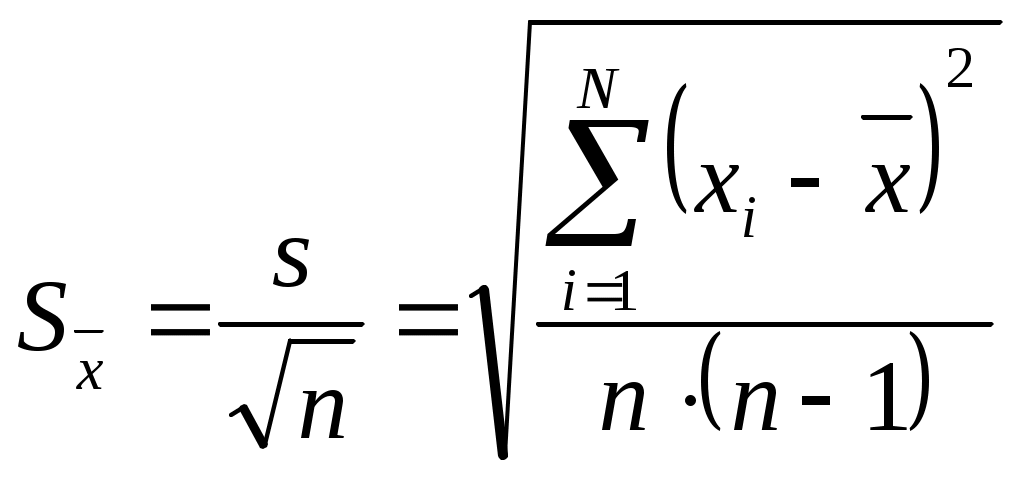
где S — средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; п — число единичных измерений в ряду.

Предельная погрешность измерения в ряду измерений (предельная погрешность) – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи. За предельную погрешность часто принимают значение 3S, то есть пр= ±3S.

Для оценки погрешности с учетом неисключенных систематических составляющих погрешностей их оценки объединяют с оценками случайных составляющих. Комплексную оценку называют суммарная средняя квадратическая погрешность результата измерений (суммарная погрешность результата; суммарная погрешность) – погрешность результата измерений, состоящая из суммы случайных и неисключенных систематических погрешностей, принимаемых за случайные.

---

Комплексную оценку вычисляют по формуле



где – средняя квадратическая погрешность суммы неисключенных систематических погрешностей при равновероятном распределении (принимаемых за случайные).

Доверительные границы суммарной погрешности (x)_могут быть вычислены по формуле



где ;

 – граница суммы неисключенных систематических погрешностей результата измерений, вычисляемая по формулам



при числе неисключенных систематических погрешностей слагаемых N ≤ 3, или, при числе слагаемых погрешностей N ≥4



где К –коэффициент зависимости отдельных неисключенных систематических погрешностей от выбранной доверительной вероятности Р при их равновероятном распределении.

Одной из современных характеристик точности измерений является неопределенность измерений (неопределенность) – параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине. К определению по РМГ 99, которое взято из VIM—93, приведены примечания, из которых следует, что параметром может быть стандартное отклонение (или число, кратное ему) или половина интервала, имеющего указанный доверительный уровень. Неопределенность, по мнению авторов документа, состоит (в основном) из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментальными стандартными отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются, на данных эксперимента или другой информации. Проблемы неопределенности измерений рассмотрены в отдельном модуле.

---

МОДУЛЬ 6. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ

Выявление и оценка погрешности измерения физической величины («суммарной погрешности» или интегральной погрешности) и ее составляющих являются традиционными задачами метрологии. Все методы выявления и оценки погрешностей можно разделить на аналитические (теоретические), экспериментальные и смешанные. Кроме того, в ряде случаев успешно используют оценки погрешностей, взятые из информационных источников. Очевидно, что данные о погрешностях, включенные в эти источники, получены с помощью теоретических расчетов или экспериментов.

Нахождение значения погрешности в информационных источниках применимо как к погрешности измерения в целом, так и к отдельным составляющим. Инструментальные погрешности средств измерений приведены в документации (включая стандарты, паспорта, аттестаты) и в справочниках. Источниками информации о погрешностях измерений могут быть такие документы, как стандартизованные или аттестованные методики выполнения измерений. Можно использовать в качестве информационных источников также отчеты о научно-исследовательских работах, монографии и другую научно-техническую литературу при достаточной степени доверия к ее авторам.

Базой аналитических методов выявления и оценки погрешностей является функциональный анализ методики выполнения измерений. Для расчетов погрешностей строят специальные аналитические модели. Моделирование обычно применяют для расчета составляющих инструментальных и методических погрешностей, а также погрешностей из-за несоответствия условий измерений нормальным. Возможно также моделирование некоторых субъективных составляющих погрешности.

Аналитические расчеты средств измеренийна точность (расчет инструментальных погрешностей) могут проводиться для оценки теоретических погрешностей преобразования измерительной информации, а также для нахождения допустимых технологических погрешностей изготовления и сборки деталей. При проектировании средств измерений такие расчеты обязательны.

Погрешности из-за отличия условий измерений от номинальных в общем случае должны учитывать воздействие влияющих величин и на средства измерений, и на измеряемые объекты. Рассмотрим, например, температурные погрешности. Для расчета воздействия влияющей величины  на объект измерения, нужно знать функцию

---