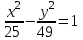Файл: Методические рекомендации по выполнению домашней контрольной работы 1 методические рекомендации по выполнению домашней контрольной работы 2.docx
Добавлен: 29.10.2023
Просмотров: 158
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ВАРИАНТ №2
Задание №1 Решить систему линейных уравнений матричным методом, методом Крамера, методом Гаусса.
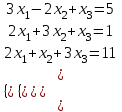
Задание №2 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
-
длину стороны АВ; -
общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых; -
косинус внутреннего угла при вершине В; -
уравнение медианы АЕ; -
уравнение и длину высоты СD; -
уравнение прямой, проходящей через точку Е параллельно стороне АВ; -
площадь треугольника АВС.
А (1,1); В (-3,3); С (-5,-2) .
Задание №3 Найти матрицу С, если: С=АВТ-АТ, А=
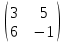 , В=
, В= 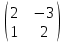
Задание №4 Построить кривые по заданным уравнениям
а) (х + 3)2 + (у – 5)2 = 4; б)
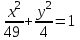 ; в)
; в) 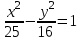 ; г) у2 = 7х.
; г) у2 = 7х.Задание №5 Вычислить пределы:
а)
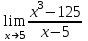 ; б)
; б) 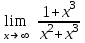 ; в)
; в) 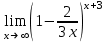
Задание №6 Найти производные функций: а)
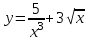 ; б)
; б) 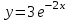 .
. Задание№7 Исследовать функцию и построить график:
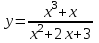 .
.Задание №8 Найти экстремумы функций двух переменных
z = x3 – y3.
ВАРИАНТ №3
Задание №1 Решить систему линейных уравнений матричным методом, методом Крамера, методом Гаусса.
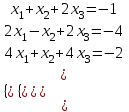
Задание №2 Найти матрицу С, если: С=АТВ-ВАТ, А=
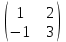 , В=
, В= 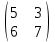 .
.Задание №3
На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
-
длину стороны АВ; -
общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых; -
косинус внутреннего угла при вершине В; -
уравнение медианы АЕ; -
уравнение и длину высоты СD; -
уравнение прямой, проходящей через точку Е параллельно стороне АВ; -
площадь треугольника АВС.
А (1,2); В (-2,3); С (-2,-3).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 1)2 + (у – 2)2 = 16; б)
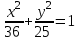 ; в)
; в) 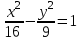 ; г) у2 = 5х.
; г) у2 = 5х.Задание №5 Вычислить пределы:
а)
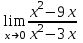 ; б)
; б) 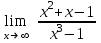 ; в)
; в) 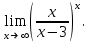
Задание №6 Найти производные функций: а)
 ; б)
; б) 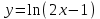 .
.Задание№7 Исследовать функцию и построить график:
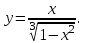
Задание №8 Найти экстремумы функций двух переменных
z = 6x2у + 2у3 – 24х – 30у.
ВАРИАНТ №4
Задание №1 Решить систему линейных уравнений матричным методом, методом Крамера, методом Гаусса.
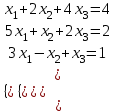
Задание №2 Найти матрицу С, если: С=АВТ-3В, А=
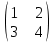 , В=
, В= 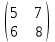 .
. Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
-
длину стороны АВ; -
общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых; -
косинус внутреннего угла при вершине В; -
уравнение медианы АЕ; -
уравнение и длину высоты СD; -
уравнение прямой, проходящей через точку Е параллельно стороне АВ; -
площадь треугольника АВС.
А (2,1); В (-3,2); С (-1,-4) .
Задание №4 Построить кривые по заданным уравнениям
а) (х − 3)2 + (у + 4)2 = 25; б)
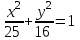 ; в)
; в) 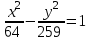 ; г) у
; г) у
2 = 16х.
Задание №5 Вычислить пределы:
а)
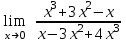 ; б)
; б) 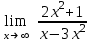 ; в)
; в) 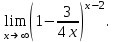
Задание №6 Найти производные функций: а)
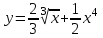 ; б)
; б) 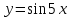
Задание№7 Исследовать функцию и построить график:
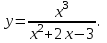
Задание №8 Найти экстремумы функций двух переменных
z = x3 – 8у3 – 6ху + 1.
ВАРИАНТ №5
Задание №1 Решить систему линейных уравнений матричным методом, методом Крамера, методом Гаусса.
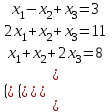
. Задание 2 Найти матрицу С, если: С=2АТВ-ВАТ, А=
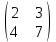 , В=
, В= 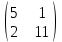 .
.Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
-
длину стороны АВ; -
общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых; -
косинус внутреннего угла при вершине В; -
уравнение медианы АЕ; -
уравнение и длину высоты СD; -
уравнение прямой, проходящей через точку Е параллельно стороне АВ; -
площадь треугольника АВС.
А (1,3); В (-2,2); С (-3,-5).
Задание №4 Построить кривые по заданным уравнениям
а) (х + 3)2 + (у + 3)2 = 4; б)
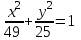 ; в)
; в) 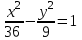 ; г) у2 = 3х.
; г) у2 = 3х.Задание №5 Вычислить пределы:
а)
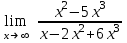 ; б)
; б) 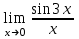 ; в)
; в) 
Задание №6 Найти производные функций: а)
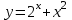 ; б)
; б) 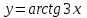
Задание№7 Исследовать и построить график:
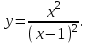
Задание №8 Найти экстремумы функций двух переменных
z = x3 – ху2 + 3х2 + у2 – 1.
ВАРИАНТ №6
Задание №1 Решить систему линейных уравнений матричным методом, методом Крамера, методом Гаусса.
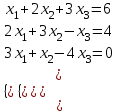
Задание №2 Найти матрицу С, если: С=(В+АВ)Т, А=
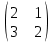 , В=
, В=  .
.Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
-
длину стороны АВ; -
общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых; -
косинус внутреннего угла при вершине В; -
уравнение медианы АЕ; -
уравнение и длину высоты СD; -
уравнение прямой, проходящей через точку Е параллельно стороне АВ; -
площадь треугольника АВС.
А (3,1); В (-3,1); С (2,-3).
Задание №4 Построить кривые по заданным уравнениям
а) (х − 1)2 + (у + 2)2 = 1; б)
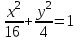 ; в)
; в) 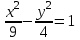 ; г) у2 = 4х.
; г) у2 = 4х.Задание №5 Вычислить пределы:
а)
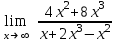 ; б)
; б) 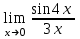 ; в)
; в) 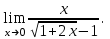
Задание №6 Найти производные функций: а)
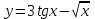 ; б)
; б) 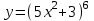 .
. Задание№7 Исследовать функцию и построить график:
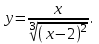
Задание №8 Найти экстремумы функций двух переменных
z = x2у –
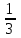 у3 + 2х2 + 3у2 – 1.
у3 + 2х2 + 3у2 – 1.ВАРИАНТ №7
Задание №1 Решить систему линейных уравнений матричным методом, методом Крамера, методом Гаусса.
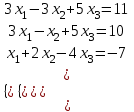
Задание №2 Найти матрицу С, если: С=(А-ВА)Т, А=
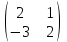 , В=
, В=  .
. Задание №3 На плоскости даны три точки А, В, С. Найти методами векторной алгебры:
-
длину стороны АВ; -
общие уравнение сторон АВ и ВС и угловые коэффициенты этих прямых; -
косинус внутреннего угла при вершине В; -
уравнение медианы АЕ; -
уравнение и длину высоты СD; -
уравнение прямой, проходящей через точку Е параллельно стороне АВ; -
площадь треугольника АВС.
А (2,2); В (-1,3); С (0,-5).
Задание №4 Построить кривые по заданным уравнениям
а) (х − 3)2 + (у – 2)2 = 9; б)
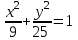 ; в)
; в)