Файл: Формирование у младших школьников представлений о площади фигуры.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 270
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Елецкий государственный университет имени И.А. Бунина»
Институт психологии и педагогики
Кафедра начального образования и социальных технологий
ФОРМИРОВАНИЕ У МЛАДШИХ ШКОЛЬНИКОВ ПРЕДСТАВЛЕНИЙ О ПЛОЩАДИ ФИГУРЫ
Выпускная квалификационная работа
обучающегося 4 курса
по программе бакалавриата: 44.03.01 Педагогическое образование
направленность (профиль): Начальное образование
(очной формы обучения)
Федяниной Анастасии Сергеевны
Руководитель – старший преподаватель
Елец – 2017
Оглавление
| Введение……………………………………………………………......... | 3 |
| Глава 1. Общие вопросы методики формирования у младших школьников представлений о величинах………………………….. | 6 |
| 6 |
| 11 |
| 16 |
| Глава 2. Формирование у младших школьников представлений о площади фигуры…………………………………………………….. | 27 |
| 2.1. Методика изучения площади фигуры в начальных классах…………………………………………………………………... | 27 |
| 2.2. Характеристика знаний и способов действий учащихся по теме «Площадь фигуры» …………………………………………………….. | 33 |
| 2.3. Методические рекомендации по формированию у учащихся представлений о площади …...…………………………………………. | 44 |
| Заключение……………………………………………………………… | 57 |
| Литература.………………………………………………………………. | 60 |
| Приложение №1. Протоколы уроков………………………………... | 65 |
| Приложение №2. Анкеты для учителей…………………………….. | 66 |
| Приложение №3. Проверочные контрольные работы……………. | 67 |
| | |
Введение
Актуальность вопросов методики изучения величин в курсе математики начальной школы обусловлена, во-первых, тем, что понятие «величина» наряду с понятием «число» является ключевым понятием, и формирование представлений о величинах имеет огромное значение для умственного развития младших школьников, усвоения ими полноценных знаний об окружающей действительности и приобретения практических умений и навыков, необходимых человеку в его повседневной деятельности.
Во-вторых, величина – это общепредметное понятие, которое находит свое применение в различных образовательных областях: «Информатика», «Человек», «Общество», «Природа», «Технология» и др. В связи с этим работа с величинами становится общеучебным универсальным умением, необходимой компетенцией.
Кроме того, знания и умения, связанные с величинами и полученные в начальной школе, становятся основой для дальнейшего изучения математики.
В соответствии с требованиями Федерального государственного образовательного стандарта НОО второго поколения в программу начального курса математики включен не только раздел «Числа и величины», но и раздел «Геометрические величины». Это делает особо актуальными вопросы, связанные с формированием у школьников представлений о длине и площади.
Основные аспекты проблемы формирования у младших школьников представлений о величинах рассмотрены в работах М.А. Бантовой, А.М. Пышкало, С.А. Альперович, М.В. Богданович, Н.Б. Истомина, А.В. Тихоненко, Ю.В. Трофименко и других ученых - методистов.
Однако, как свидетельствует анализ изученных нами работ, вопрос о разработке методик, направленных не только на формирование четких и осознанных представлений учащихся о такой величине как «площадь фигуры», но и активизирующих их учебную деятельность, был решен недостаточно полно. Кроме того, в практике работы начальной школы имеет место факт некорректного использования соответствующей терминологии, использования однообразных по характеру познавательной деятельности заданий.
Учитывая необходимость развития у младших школьников интереса к изучаемому предмету, понимания математики как части общечеловеческой культуры, целесообразно, на наш взгляд, включать в учебный процесс элементы истории математики, которые помогут учителю начальных классов полнее и глубже раскрыть содержание изучаемых понятий, законов, математических фактов.
Исходя из этого, необходимо искать эффективные пути совершенствования методики изучения величин, в том числе и площади, в процессе не только урочной, но и внеурочной деятельности.
Все вышеизложенное обусловило выбор темы нашего исследования, позволило выявить проблему и наметить пути ее решения.
Проблема исследования: каковы педагогические условия эффективного формирования у младших школьников представлений о величине.
Цель: изучить процесс формирования у младших школьников представлений о площади фигуры и выявить пути повышения его эффективности.
Объект исследования: процесс формирования у младших школьников представлений о величинах.
Предмет исследования:деятельность учителя по формированию у младших школьников представлений о площади фигуры и деятельность учащихся в этом процессе.
Гипотеза исследования состояла в предположении: использование в процессе формирования у младших школьников представлений о площади исторических сведений, заданий практического и развивающего характера будет способствовать расширению математического кругозора учащихся и обеспечит повышение качества их знаний и способов действий.
Задачи:
1) изучить психолого-педагогическую литературу по проблеме;
2) раскрыть математические основы изучения величин в начальном курсе математики;
3) изучить практику работы школы по формированию у младших школьников представлений о площади;
4) разработать методические рекомендации по повышению эффективности процесса формирования у младших школьников представлений о площади фигуры.
Методы: анализ научно-методической литературы и письменных работ обучающихся, педагогическое наблюдение, анкетирование, педагогический эксперимент, обобщение.
База исследования: 4 г класс МБОУ «Лицей №5 г. Ельца», учитель Алешина Галина Николаевна.
Структура дипломной работы включает в себя две главы, выводы по ним, заключение, литература, приложение.
Глава 1. Общие вопросы методики формирования у младших школьников представлений о величинах
-
Математические основы изучения величин
в начальных классах
Существенная особенность окружающей нас действительности – беспрерывные и многообразные ее изменение. Меняется погода, возраст человека, изменяются условия жизни людей, животный и растительный мир. Для того чтобы дать научное объяснение этим процессам, нужно знать их определенные свойства, например, такие, как время, масса, площадь. Все названные свойства - это величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием.
Величины – это особые свойства реальных объектов или явлений. Например, свойство предметов иметь протяженность называется длиной. Это же слово мы употребляем, когда говорим о протяженности конкретных объектов. Поэтому про длины конкретных объектов говорят, что это величины одного рода. Вообще однородные величины выражают одно и тоже свойство объектов некоторого множества. Разнородные величины выражают различные свойства объектов. Например, длина и площадь — это разнородные величины.
Представление о площади фигуры имеет любой человек: мы говорим о площади комнаты, площади земельного участка, о площади поверхности, которую надо покрасить, и т.п. При этом мы понимаем, что если земельные участки одинаковы, то площади их равны; что у большего участка площадь больше; что площадь квартиры слагается из площади комнат и площади других ее помещений.
Это обыденное представление о площади используется при ее определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют особый класс фигур. Например, рассматривают площади многоугольников и других ограниченных выпуклых фигур, или площадь круга, или площадь поверхности тел вращения и т.д. Мы будем говорить только о площади многоугольников и ограниченных выпуклых плоских фигур.
Площадью фигуры называется неотрицательная величина, определенная для каждой фигуры так, что:
1) равные фигуры имеют равные площади;
2) если фигура составлена из конечного числа фигур, то ее площадь равна сумме их площадей [38, с. 278].
Величины – длина, площадь, масса и другие обладают рядом свойств:
-
Любые две величины одного рода сравнимы: они либо равны, либо одна меньше другой. Иными словами, для величин одного рода имеют место отношения «равно», «меньше», «больше» и для любых величин a, b справедливо одно и только одно из отношений: a>b, a<b, a=b. Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем длина любого катета этого треугольника, масса яблока меньше массы арбуза, а длины противоположных сторон равны. -
Величины одного рода можно складывать, в результате сложения получится величина того же рода. Другими слова, для любых двух величин а и bоднозначно определяется величина a + b, ее называют суммой величин a и b. Например, если а - длина отрезка AB, b - длина отрезка ВС (рис.1), то длина отрезка АС есть сумма длин отрезков АВ и ВС [38, с. 280]. -
Величину умножают на действительное число, получаю в результате величину того же рода. Другими словами, для любой величины а любого неотрицательного действительного числа x существует единственная величина b = ха; величину b называют произведением величины а на число х. Например, если длину а отрезка АВ умножить на х = 2, то получим длину 2а нового отрезка АС (рис.2). -
Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и bназывается такая величина с, что а=b+с. Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а = b + с. Например, если а - длина отрезка АС, b - длина отрезка АВ, то длина отрезка ВС есть разность длин отрезков АС и АВ. -
Величины одного рода делят, определяя частное через произведение величины на число: частным величин а и b называется такое неотрицательное действительное число х, что а = хb. Чаще это число х называют отношением величин а и b и записывают в таком виде: а:b = х. Например, отношение длины отрезка АС к длине отрезка АВ равно 2 (рис.2).
A B C А В С

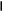
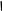
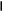

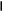
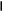
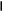
Рис.1 Рис.2
Сравнивая величины непосредственно, мы можем установить их равенство или неравенство. Чтобы получить более точный результат сравнения, например, узнать, насколько масса одного тела больше массы другого, необходимо величины измерить. Измерение заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей – другой, для массы – третий и т.д. Но каким бы не был этот процесс, в результате измерения величина получает определенное численное значение при выбранной единице.
Вообще если дана величина а и выбранная единица величины е, то в результате измерения величины а находят такое действительное число х, что а= хe. Это число х называют численным значением величины a при единице величины e.
Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, за единицу площади принимают площадь квадрата со стороной, равной единичному отрезку е, т.е. отрезку, выбранному в качестве единицы длины. Площадь квадрата со стороной е обозначают е2. Измерение площади состоит в сравнении площади данной фигуры с площадью единичного квадрата е2. Результатом этого сравнения является такое число х, что S (F) = xe2. Число х называют численным значением площади при выбранной единице площади.
Одним из приемов, опирающихся непосредственно на определение площади, является измерение площади при помощи палетки — сетки квадратов, нанесенной на прозрачный материал.
Согласно определению, любую величину можно представить в виде произведения некоторого числа и единицы этой величины. Например, 7кг = 7 х 1кг, 12см = 12 х 1см, 3ч= 3 х 1ч.
Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной величины к другой.