На вопрос о повышении познавательного интереса посредством знакомства учащихся с историей измерений все учителя дали положительный ответ.

Учитывая вышесказанное, полагаем, что знакомство с историей измерений при отсутствии или небольшом количестве подобного материала в учебниках математики для начальной школы целесообразно реализовать во внеклассной работе.

Анализ результатов проверочных работ учащихся (см. Приложение №3) позволил выявить следующие пробелы в знаниях учащихся при изучении данной темы:

- дети путают единицы площади и длины;

-имеют слабые представления об измерениях площадей, осуществляемых в повседневной жизни;

- практически не имеют понятия об исторических единицах измерения площади и длины;

- не имеют четкого представления о том, какие единицы измерения площади целесообразно применить в конкретных условиях;

- не умеют вычислять площадь прямоугольника при решении задач;

- не до конца выполняют задание.

Результаты проверочной работы показали (см. Диаграмма 1), что с заданием №1 справилось 22 ученика (91%), не справились – 2 (9%). Кочеткова Д. не правильно записала величины в порядке возрастания, а Чурсин Д. вовсе не смог выполнить данное задание.

Задание №2 без ошибок выполнили 22 учащихся (91%), с ошибками – 2 учащихся (9%). Башкатова А. и Кочеткова Д. перепутали единицы измерения для дома и футбольного поля.

Умение, проверяемое при выполнении задания №3, не сформировано у 11 учащихся (46%). Эти дети не смогли «на глаз» определить, какова примерно площадь объектов (Марных Д. определила площадь класса в 42 км², у Коротеевой Е. площадь тетради равна 15 см², у Иванова А. площадь школьной доски – 300 см²), 13 детей успешно справились с заданием (54%).

С заданием №4 справилось 6 учащихся (25%), не справилось – 18 (75%). Большинство детей не знают исторические единицы измерения длины и площади, поэтому допустили ошибку в этом задании.

Задание №5 без ошибок выполнили 9 учеников (38%), с ошибками – 15 учащихся (62%). В данном задании необходимо было продолжить ряд величин. Некоторые дети продолжили лишь, дописав по одной величине, часть учащихся дополнили с ошибками (мм, см², м²).

Умение, проверяемое при выполнении задания №6, не сформировано у 6 учащихся (25%), в основном у этих школьников плохо сформированы вычислительные навыки (например, у Бахаевой Е. произведение 15 и 15 равно 205, а Марных Д. при умножении 15 на 15 получила 155), 18 человек справились (75%).

С заданием №7 справилось 23 учащихся (96%), не справилось – 1 (4%).

---

Задание №8 без ошибок выполнили 18 учащихся (75%), с ошибками – 6 учащихся (25%). Некоторые учащиеся класса допускают вычислительные ошибки (например, Наумов Н. при вычислении (7 х 7 + 7 х 7) получил 96).

Таким образом, мы видим, что в изучении данной темы учитель уделяет большее внимание развитию вычислительных навыков детей, упуская развитие умений практического применения знаний о площади, связи этих знаний с повседневной жизнью и бытовыми предметами (об этом свидетельствуют ошибки учащихся при выполнении заданий №2, №3 проверочной работы), развитие логического мышления (№4, №7), умение вычислять площадь прямоугольника по известным сторонам квадратов, из которых составлен прямоугольник (№8).

Кроме того, у учащихся исследуемого класса вызывают затруднения задания, в которых необходимо использовать не только приобретенные знания и умения, но и способы умственных действий.
Диаграмма 1

Результаты проверочной работы учащихся

экспериментального класса



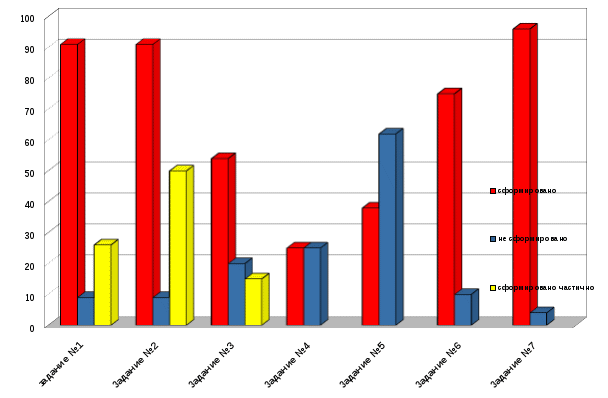
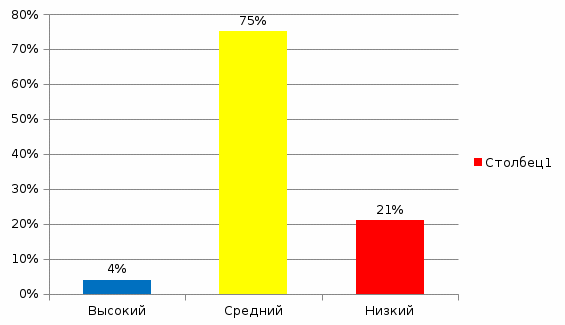
Диаграмма 2

Уровнь обученности учащихся экспериментального класса


Для определения продуктивности обучения по теме «Площадь фигуры» мы использовали показатель усвоения (продуктивности обучения), предложенный И.П. Подласым:

О = (Ф / П) · 100 %, где О – оценка обученности (продуктивности), Ф – фактический объем усвоенных знаний, умений, П – полный объем знаний, умений, предложенных для усвоения [28, с. 548].

По результатам выполненных проверочных работ учащимися экспериментального класса мы выделили уровни их обученности по теме (см. Диаграмму 2) и получили следующую общую оценку обученности:

О = (238 / 408) · 100 % = 58,33%

Для исправления этого положения необходимы, на наш взгляд, задания развивающего и практического характера на сравнение площадей окружающих предметов (книг, крышки стола и т.п.); задачи, которые помогут учащимся установить взаимосвязь между геометрическими фигурами, их построением и вычислением площади геометрических фигур; задания, связанные с историческими единицами измерения площади и длины.

Некоторые рекомендации по повышению эффективности процесса формирования представлений о площади фигуры мы предлагаем в следующем параграфе работы.

---

2.3. Методические рекомендации по формированию

у учащихся представлений о площади фигуры

Для преодоления выявленных трудностей, с которыми сталкиваются учащиеся при изучении площади фигуры, необходимо работать не только над формированием представлений о данной величине, но и над осознанием практической значимости изучаемых понятий, расширять кругозор младших школьников. Следует чаще обращать внимание детей на взаимосвязь математики с практической деятельностью людей, учить видеть не только абстрактность математики, но и ее практическую востребованность в повседневной жизни.

Решению указанных задач будут способствовать задания развивающего характера:

1. Д орисуй фигуру так, чтобы получился прямоугольник, площадь которого равна 15 см²

2. 
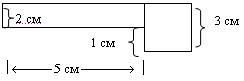
   Найди площадь квадрата АВСD_______ см².
   

Закрась 20 см² - синим цветом, 5 см² - красным цветом, 30 см² - зеленым цветом. Какая площадь осталась не закрашенной?



3. Во сколько раз увеличится площадь прямоугольника, если его длина увеличится в 2 раза, а ширина не изменится? Во сколько раз уменьшится площадь прямоугольника, если его ширина уменьшится в 4 раза, а длина не изменится? Во сколько раз площадь одного квадрата больше площади другого квадрата?

4. В прямоугольнике АВСD закрась красным цветом фигуры, площади которых равны площади треугольника МКЕ:



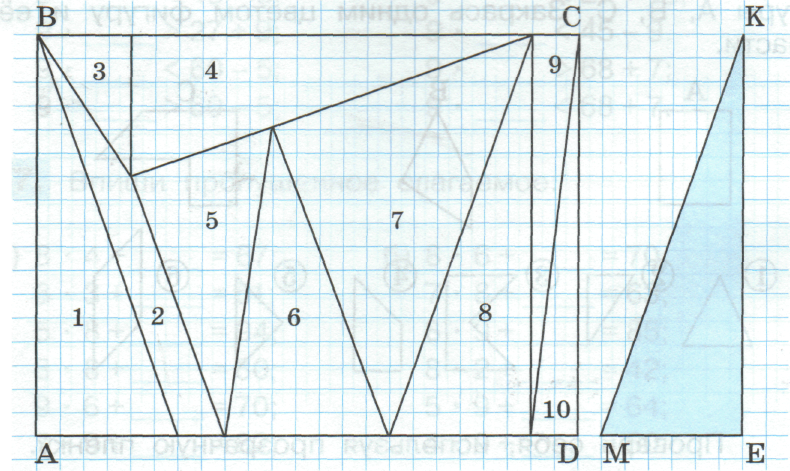
5. Заполни таблицу:

Длина	7 см	6 см		4 см
Ширина		2 см	3 см
Площадь	7 см²		15 м²	16 см²

---

- Могут ли разные прямоугольники иметь равные периметры?

- У какого из таких прямоугольников самая большая площадь?

- Могут ли разные прямоугольники иметь равные площади?

- Если могут, то начерти разные прямоугольники, площадь которых будет равна 16 см².

Необходимо уделять время на уроках заданиям творческого характера, связанных с геометрическими фигурами, периметром и площадью. Такие задания помогают развивать логическое мышление, внимание и сообразительность, а также формируют интерес к геометрии.

К таким заданиям можно отнести:

1. 
   Посчитай и запиши в клетки соответствующее количество квадратов, треугольников и прямоугольников.
   

2. 
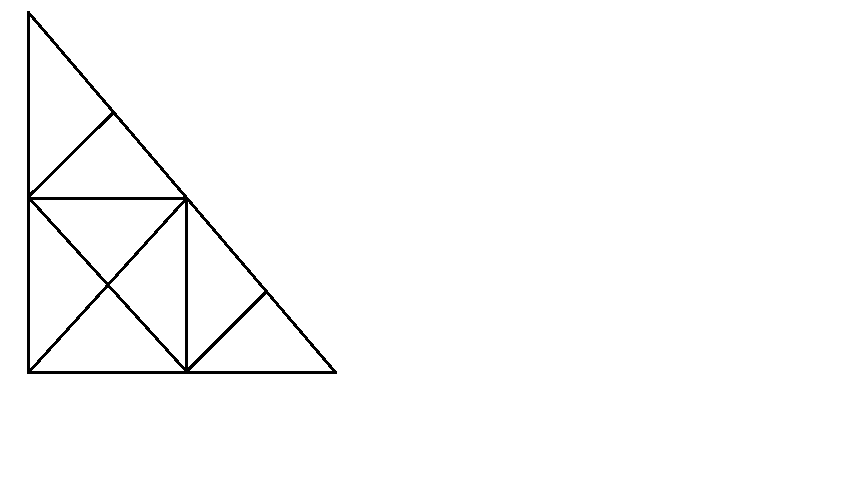
   Объясни, почему от перестановки фигур образовалось пустая клетка?
   

3. 
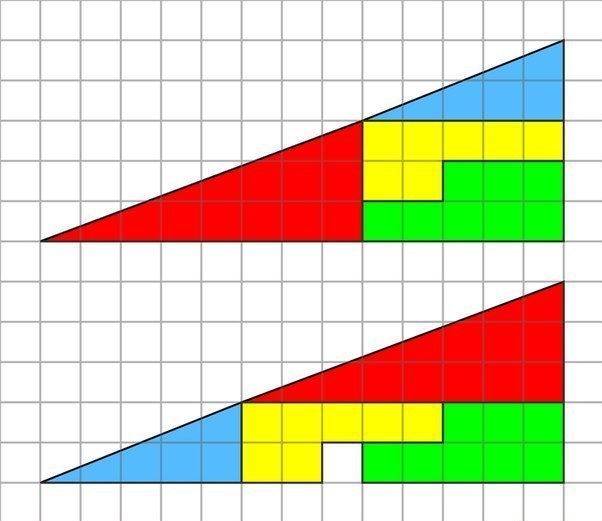
   Какая фигура имеет большую площадь?
   

а) б) в)


Закрепить знания наименований единиц площади и соотношений между ними помогут задания практического характера:

1. Допиши единицы измерения: площадь оконного стекла 8400…; площадь поверхности карты 4500…, площадь поверхности обложки книги 340… .

2. Ученик правильно выполнил измерения, но не записал соответствующих единиц. Допиши их.

А) площадь классной комнаты 24…;

Б) площадь поверхности стола 84…;

В) площадь поверхности обложки тетради 320…

3. Найди ошибки в обозначении единиц измерения:

А) площадь комнаты 14 м²;

Б) площадь школьного коридора 37 м²;

В) площадь школьного двора 200 дм².

4. Измерение площадей моделей прямоугольников.

5. Практиковать определение площадей фигур прямоугольной формы «на глаз», с последующей проверкой.

6. Выберите единицы измерения для площади поля, пенала, крыши дома, города и крышки стола.

7. Площадь одной из комнат трехкомнатной квартиры равна 20 м², а площадь второй – на 4 м² меньше. Площадь первых двух комнат на 17 м² больше площади третьей комнаты. Какова площадь третьей комнаты?

---

8. Длина стороны зеркала квадратной формы 10 дм. Скольким квадратным метрам будет равна площадь отражения лица царевны Несмеяны, если, когда она любуется собой, это отражение занимает как раз всю площадь зеркала?

9. Зал, где находится Коля, имеет форму прямоугольника, длина которого 22 м, а ширина в 2 раза меньше. Площадь второго зала в 2 раза больше первого зала. Найдите площадь всего дворца.

При работе над темой «Площадь» учитель может использовать систему упражнений, раскрывающую некоторые свойства понятия площади фигуры, а также подтверждающая справедливость математических законов и для данной величины.

I. Упражнения, которые иллюстрируют упорядоченность множества площадей фигур отношением «иметь меньшую площадь».

- Площадь какой фигуры, изображенных на рис. 1, меньше? Площадь квадрата меньше площади круга, так ли это? (Свойство асимметричности отношения «меньше» на множестве площадей геометрических фигур.)

- Верно ли, что площадь круга (рис. 2) меньше площади прямоугольника? (Свойство антирефлексивности отношения «меньше» на множестве площадей геометрических фигур).

- Сравните площади фигур.



Рис.1 Рис.2

При помощи наложения фигур ученики устанавливают, что площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника. Дети убеждаются, что площадь квадрата меньше площади прямоугольника. Педагог, подводя итоги этой работы, говорит: «Площадь квадрата меньше площади прямоугольника, так как площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника».

II. Упражнения, приводящие к понятию площади фигуры.

• 
  На сколько квадратных сантиметров площадь квадрата со стороной 4 см меньше площади квадрата со стороной 7 см? (Существование разности площадей.)
  

III. Упражнения, которые иллюстрируют переместительное свойства сложения площадей фигур.

• 
  Найдите площадь данной фигуры.
  

---

Смотрите также файлы

• Практическая работа по Основы экологическго права дисциплине Выполнил(а) студент(ка).docx

• Практическая работа 1 Выполнил(а) Укажите фамилию, инициалы, место работы.docx

• Долгосрочная цель Увеличить доходность бизнеса до 1 млн в месяц к концу 5 лет.docx

• Урока. Тема урока Нравственные уроки сказки К. Г. Паустовского Теплый хлеб. ( Чему учит сказка К. Г. Паустовского Тёплый хлеб ).docx

• Актуальные проблемы теории и методики дошкольногообразования.pdf