Учитель вместе с учащимися составляет выражения:

1. 
   2 х 5 + 3 х 3 (см²) – площадь данной фигуры;
   
2. 
   3 х 3 + 2 х 5 (см²) – площадь этой же фигуры. В результате вычислений устанавливается, что 2 х 5 + 3 х 3 = 3 х 3 + 2 х 5.
   

Решение таких заданий еще раз подтверждает переместительное свойство сложения во множестве площадей фигур.

IV. Упражнения, которые иллюстрируют сочетательное свойство сложения площадей фигур.



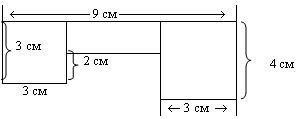
Необходимо найти площадь фигуры различными способами. Дети вместе с учителем составляют выражения:

1. 
   (3 х 3 + 3 х 1) + 4 х 3 (см²)
   
2. 
   3 х 3 + (3 х 1 + 4 х 3) (см²)
   

Ученики устанавливают, что сложение величин ассоциативно, вычисляя значения этих выражений.

V. Задания, неоткрыто вводящие свойство площади фигуры: площадь фигуры можно разделить на некоторое число n одинаковых частей.

Измерение площади при помощи палетки доказывает то, что всякую площадь можно разделить на несколько одинаковых частей.

Площадь определяется как свойство плоских предметов среди других свойств. Ученики начальной школы уже до исследования темы сопоставляют объекты по площади и верно устанавливают отношения «>», «<», «=», если сравниваемые предметы резко отличаются друг от друга или совершенно одинаковые.

При продумывании содержания начального курса математики надо помнить, что необходимо формировать целостное мировоззрение, определяющее сущность внутреннего мира личности. Именно целостность мировоззрения позволяет ученику чувствовать себя достойным представителем своей культуры.

Целесообразно строить обучение таким образом, чтобы содержательно имелась связь с принципом: мой край, моя Родина, весь мир. Можно использовать задания, где используются числовые характеристики своего края, других регионов России и разных стран. Обращаясь к краеведческому и историческому аспекту величин, можно давать краткие исторические справки и факты:

1. В Риме мерой полей служила единица югер. Это ярмо, т.е. деревянная рама, которую надевали на шеи двум волам. Югер означал участок земли, вспаханный за день плугом, в который впряжена пара волов. Аналогичная мера земли существовала и на Руси в XI – XIII в.в. – плуг (примерно 8 – 9 гектаров)». Для измерения площади в дореволюционной России использовали десятину. 1 десятина = 10930 м² или примерно 1,1 гектара».

---

2. Великий русский писатель Лев Николаевич Толстой (1828 – 1910) проявлял особый интерес к математике и ее преподаванию, много лет преподавал начала математики в основанной им же Яснополянской школе. Написал оригинальную «Арифметику» и «Руководство для учащихся». Своим гостям Л.Н. Толстой нередко предлагал интересные задачи, среди которых находится следующая: «Косцы должны выкосить два луга. Начав с утра косить большой луг, они после полудня разделились: одна половина осталась на первом лугу и к вечеру его докосила, а другая перешла косить на второй луг, площадью вдвое меньше первого. Сколько было косцов, если известно, что в течение следующего дня, оставшуюся часть работы выполнил один косец?

Сведения краеведческого характера также могут способствовать развитию интереса детей к величине площади.

Например, можно познакомить детей с фактами истории Липецка, связанными с деятельностью Петра I. Так, из документов известно, что для преобразования поселка Липецкие Заводы в г. Липецк был составлен генеральный план. На месте запутанной сетки улиц была запроектирована совершенно новая сетка совершенно одинакового размера прямоугольных кварталов, размещенных по обе стороны речки Липовки. Единственная центральная площадь города размером 300 х 300 метров размещалась на правом берегу Липовки.

Полагаем, что для повышения интереса детей к изучению темы, можно воспользоваться более подробной информацией по истории края и положить информацию о размерах старинной застройки города, площади и т.п. в основу занимательных задач, которые могут быть включены в урок, во внеурочную деятельность (например, игра-путешествие, интегрирующая математику и краеведение).

Например, известен также факт о существовании в Липецких заводах деревянной конторы Петра I. В архивах имеются ее чертежи и размеры: 23 аршина длины, 10 аршин ширины, 4 высоты. Для образования водохранилища с достаточным устойчивым запасом воды перехватываются воды речки Студенки, Монастырские ключи, Липовки – создается огромная плотина – «длина 1100 сажен, ширина 11 ½ сажен, вышина 5 ½ аршина, от воды биты сваи сосновые; ко оным сваям прибиты пласты сосновое железным гвоздем» [33, с. 46].

Эти данные могут быть использованы для различных упражнений на уроках изучения площади: перевода старинных мер в современные единицы измерения; для нахождения площади исторической постройки. Например,

---

1. 
   Вознесенский Собор построен в 1888 году на Красной площади - центральной части г. Ельца. Ширина равна 34 м, а длина на 50 м больше. Найдите периметр и площадь Собора.
   

2) Стройка высоководного Каракумовского моста началась в 1931 году. Его ширина составила 3 м, а длина в 66 раз больше. Найдите площадь моста.

3) Дом Т.Н. Хренникова в Ельце упоминается с 1901 года, площадь которого равна 221 м². Найдите периметр и длину, если ширина равна 13 м.

4) Площадь территории США 9 млн. км². На сколько она меньше территории России, если площадь России равна 17млн. км²?

5) Найдите длину дороги, которая равна 5 верстам. Если 1 верста = 1 км 60 м.

6) Вычеркни лишнюю единицу измерения: соха, плуг, гектар, верста, колодец. Объясни почему.

Такие задачи, безусловно, расширяют кругозор учащихся, а также воспитывают патриотизм и любовь к Родине. Целесообразно предложить детям самостоятельно составить подобные задачи и наиболее удачно составленные решить в классе со всеми детьми.

Кроме того, исторические сведения о площади и других величинах могут использоваться при организации внеурочной деятельности младших школьников, например, при проведении внеклассных мероприятий по математике (конкурс, турнир, викторина или игра-путешествие). В качестве примера приведем примерные задания для математического турнира.

Тур 1 «Разминка»

Назовите общий признак фигур. (Каждой команде дается по три варианта)

а) (Незамкнутые)

б)

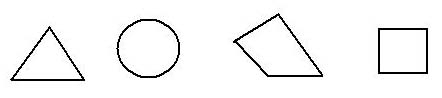
(Наличие углов и сторон)

в)

(Геометрические фигуры)

Тур 2 «Реши ребус»

Участникам каждой группы даются ребусы. Выигрывает та команда, которая справиться быстрее и правильно.

---

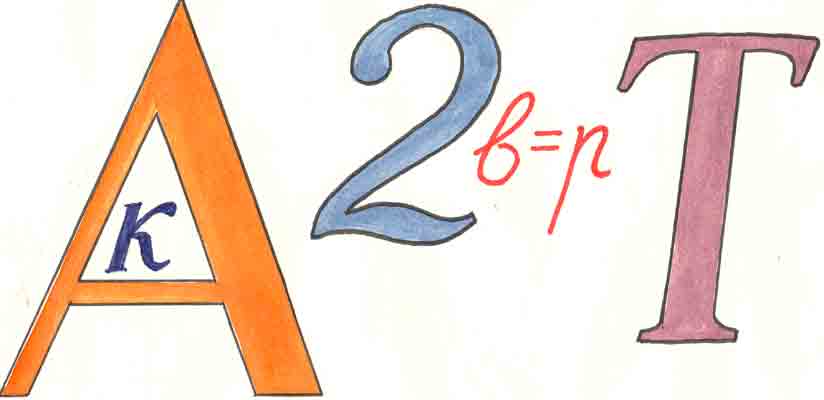
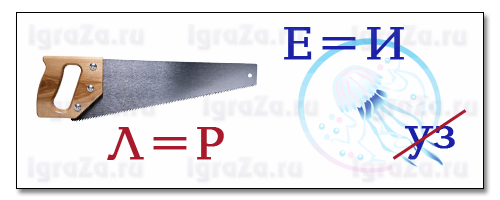
Тур 3 «Посчитай»

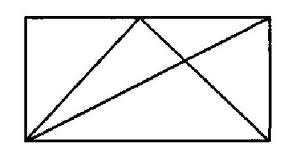
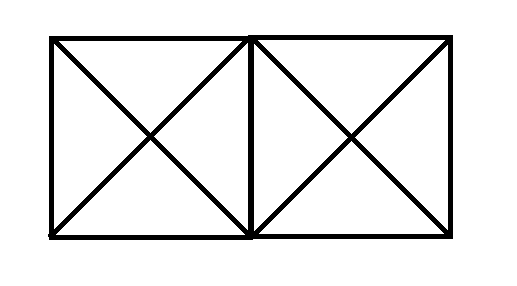
Командам дается рисунок, на котором изображены геометрические фигуры. Необходимо посчитать сколько на нем геометрических фигур. А затем показать сумма площадей каких фигур равна площади каждого прямоугольника.



Тур 4 «Задачка»

1. 
   8 июня 1915 года была закончена знаменитая картина Казимира Малевича «Черный квадрат». Найдите площадь и периметр квадрата, если его сторона равна 80 см. (Площадь – 6400 кв. см, периметр – 320 см)
   
2. 
   В 1936 году был построен стадион «Динамо» в Ельце, А позднее переименован в стадион «Труд». Найдите его площадь, если ширина поля 62 м, а длина – 103 м. (6386 кв. м)
   
3. 
   Кафедральный соборный храм Христа Спасителя в Москве построен в 1990 году. Он имеет длину 80 м, а ширину 55 м. Найдите площадь храма. (4400 кв. м)
   

Тур 5 «Кроссворд»



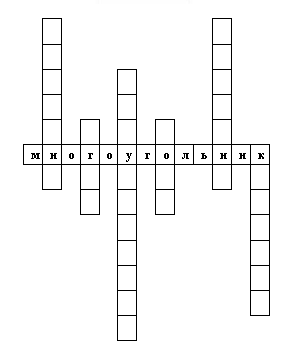
Вопросы к кроссворду:

1. 
   Точка, из которой исходят лучи.
   
2. 
   Уголь, без “ь”.
   
3. 
   Фигура, у которой 3 угла, 3 стороны, 3 вершины.
   
4. 
   Фигура, у которой 4 стороны и противоположные углы равны.
   
5. 
   Как называются лучи, образующие угол?
   
6. 
   Фигура, у которой все стороны равны.
   

Тур 6 «Изобрази фигуру»

Командам даются одинаковые наборы геометрических фигур. Учащиеся должны из них сложить какое-либо изображение и рассказать, что это.

Необходимо постоянно проводить межпредметные связи на уроках. Так, например, на уроках технологии можно предложить детям сделать аппликацию из плоских геометрических фигур или групповой проект картины из объемных фигур. На уроках информатики с помощью геометрического редактора создать рисунок. На уроках окружающего мира во время экскурсии обратить внимание на площади окружающих предметов и определить ее «на глаз».

Для закрепления целесообразно давать детям задания для самостоятельного выполнения дома. А после их выполнения сравнивать с выполненными заданиями других учащихся и исправлять допущенные ошибки. Например, можно предложить детям найти и рассказать информацию об исторических единицах измерения, определить без помощи линейки площадь каких-либо предметов (стула, мобильного телефона и т.д.), придумать творческое или развивающее задания для других учащихся класса, раздать небольшие самостоятельные с вариантами ответов и т.д.

---

Описанная выше работа отвечает, на наш взгляд, формированию нового мировоззрения в контексте гуманизации, общечеловеческой и национальной культур, обеспечивает выстраивание системы ценностей и жизненных смыслов личности, способов самовыражения, а прочность сформированного мировоззрения личности порождает устойчивый интерес к собственной культуре и культуре других народов. Кроме того, такая работа расширяет кругозор младших школьников и положительно влияет на качество формируемых знаний и способов действий.

---

Смотрите также файлы

• Практическая работа по Основы экологическго права дисциплине Выполнил(а) студент(ка).docx

• Практическая работа 1 Выполнил(а) Укажите фамилию, инициалы, место работы.docx

• Долгосрочная цель Увеличить доходность бизнеса до 1 млн в месяц к концу 5 лет.docx

• Урока. Тема урока Нравственные уроки сказки К. Г. Паустовского Теплый хлеб. ( Чему учит сказка К. Г. Паустовского Тёплый хлеб ).docx

• Актуальные проблемы теории и методики дошкольногообразования.pdf