Файл: Методические указания и контрольные задания для студентовзаочников инженернотехнических и технологических специальностей вузов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 258
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
-
Квантовое состояние
Задание состояния микрочастиц; волновая функция; ее статистический смысл. Суперпозиция состояний в квантовой теории. Амплитуда вероятностей. Объяснение поведения макрочастицы в интерферометре. Объяснение дифракции нейтронов на кристалле. Вероятность в квантовой теории.
-
Уравнение Шредингера
Временное уравнение Шредингера. Стационарное уравнение Шредингера; стационарное состояние. Частицы в одномерном и трехмерном ящиках. Частица в одномерной прямоугольной яме. Прохождение частицы над и под барьером. Гармонический осциллятор.
-
Атом
Частица в сферически симметричном поле. Водородоподобные атомы. Энергетические уровни. Потенциалы возбуждения и ионизации. Спектры водородоподобных атомов. Пространственное распределение электрона в атоме водорода. Ширина уровней. Структура электронных уровней в сложных атомах. Типы связи электронов в атомах. Принцип Паули. Периодическая система элементов Д. И. Менделеева.
-
Молекула
Молекула водорода. Обменное взаимодействие. Физическая природа химической связи. Ионная и ковалентная связи. Электронные термы двухатомной молекулы. Колебания и вращения двухатомной молекулы. Колебательная и вращательная структура термов. Колебания многоатомных молекул. Молекулярные спектры.
-
Атомное ядро
Строение атомных ядер. Феноменологические модели ядра. Ядерные реакции. Механизмы ядерных реакций. Радиоактивные превращения атомных ядер. Реакция ядерного деления. Цепная реакция деления. Ядерный реактор. Проблема источников энер- 18
гии. Термоядерные реакции. Энергия звезд. Управляемый термоядерный синтез.
-
Элементы квантовой электроники
Коэффициенты Эйнштейна для индуцированных переходов в двухуровневой системе. Принцип работы квантового генератора. Твердотельные и газоразрядные лазеры. Радиоспектроскопия. Первый мазер. Метод трех уровней. Открытый резонатор. Первые лазеры.
-
Элементы квантовой статистики
Статистическое описание квантовой системы, различие между квантовомеханической и статистической вероятностями. Теорема Нернста и ее следствия. Симметрия волновой функции многих одинаковых частиц. Квантовые идеальные газы; распределения Бозе и Ферми.
-
Конденсированное состояние
Строение кристаллов. Исследование кристаллических структур методами рентгено-, электроно-, нейтронографии. Точечные дефекты в кристаллах: вакансии, примеси внедрения, примеси замещения. Краевые и винтовые дислокации. Дислокация и пластичность.
Акустические и оптические колебания кристаллической решетки. Экспериментальное исследование колебательного спектра: звук, поглощение инфракрасного излучения в ионных кристаллах, комбинационное рассеяние, неупругое рассеяние нейтронов.
Понятие о фононах. Теплоемкость кристаллов при низких и высоких температурах. Решеточная теплопроводность. О квазиимпульсе фонона. Процессы переброса. Размерный эффект в теплопроводности кристаллов. Эффект Мессбауэра и его применение.
Электропроводность металлов. Носители тока в металлах. Недостаточность классической электронной теории. Электронный ферми-газ в металле. Носители тока как квазичастицы. Электронная теплоемкость. Элементы зонной теории кристаллов. Зонная структура энергетического спектра электронов. Уровень Ферми. Поверхность Ферми. Число электронных состояний в зоне. Заполнение зон; металлы, диэлектрики, полупроводники. Понятие дырочной проводимости. Собственные и примесные полупроводники.
Явление сверхпроводимости. Термодинамика сверхпроводников. Куперовское спаривание как необходимое условие сверхпроводимости. Кулоновское отталкивание и фононное притяже-
ние. Поверхностная энергия на границе между нормальной и сверхпроводящей фазами. Сверхпроводники первого и второго рода. Роль примесей. Высокотемпературная сверхпроводимость. Захват и квантование магнитного потока. Туннельный контакт. Эффект Джозефсона и его применение.
Магнетики. Пара-, диа-, ферро- и антиферромагнетики. Теория ферромагнетизма. Обменное происхождение молекулярного поля. Доменная структура. Техническая кривая намагничивания. Теория молекулярного поля антиферромагнетиков. Ферриты.
-
Жидкие кристаллы
Типы жидких кристаллов: нематики, холестирки, смектики. Примеры жидких кристаллов. Фазовые диаграммы. Упругие свойства нематиков. Поведение в электрическом и магнитном полях.
-
Вещество в экстремальных условиях
Вещество при сверхвысоких температурах и сверхвысоких плотностях. Металлический водород. Уравнение состояния вещества при больших плотностях. Карликовые белые звезды. Нейтронное состояние вещества. Пульсары. Вещество в сверхсильных электромагнитных полях.
-
1 2 3 4 5 6 7 8 9 ... 12
СОВРЕМЕННАЯ ФИЗИЧЕСКАЯ КАРТИНА МИРА
Вещество и поле. Атомно-молекулярное строение вещества. Атомное ядро. Кварки. Элементарные частицы, лептоны, адроны. Взаимопревращения частиц. Сильное, электромагнитное, слабое и гравитационное взаимодействия. Иерархия взаимодействий. О единых теориях материи. Физическая картина мира как философская категория.
ПРИМЕНЕНИЕ МИКРОКАЛЬКУЛЯТОРА
ПРИ РЕШЕНИИ ЗАДАЧ
Важнейшим средством совершенного научного исследования является математическое моделирование физических явлений и исследование этих моделей с помощью ЭВМ. Совершенные ЭВМ позволяют проводить сложнейшие расчеты. В некоторых областях науки, например астрофизике, проведение реальных экспериментов практически невозможно, поэтому исследователями проводится вычислительный эксперимент. ЭВМ нужны не только для проведения машинного эксперимента, но и для обработки результатов реальных экспериментов. Совершенный фи- 20
зический эксперимент часто дает столько информации, что обработать ее без ЭВМ практически невозможно.
Для решения любой задачи необходим алгоритм. Под алгоритмом понимают понятное и точное предписание ЭВМ совершать последовательность действий для достижения указанной цели или решения конкретной задачи. Всякий алгоритм строится в расчете на конкретного исполнителя. Таким исполнителем для проведения инженерных и студенческих расчетов различного вида заданий являются микрокалькуляторы семейства «Электроника». Это электронно-вычислительное устройство миниатюрных размеров индивидуального пользования. Оно может быть успешно использовано при решении задач, предлагаемых в контрольных работах. Выполняя вычисления с помощью микрокалькулятора, вы экономите время, освобождая его для изучения теоретических основ курса физики.
Прежде чем пользоваться микрокалькулятором, внимательно ознакомьтесь с руководством по эксплуатации:
-
изучите общие сведения об устройстве;
-
ознакомьтесь с правилами подготовки его к работе.
Рассмотрим решение следующих задач с применением микрокалькулятора.
-
Вычислить эффективный диаметр молекул азота, если его критическая температура 126 К, критическое давление 3,40 МПа.
Дано: 7^=126 К; ^ = 3,40 106 Па.
Найти: d.
Решение. Азот, согласно условию задачи, должен подчиняться уравнению Ван-дер-Ваальса:
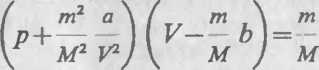
Постоянную b в уравнении Ван-дер-Ваальса с достаточной степенью точности считают равной учетверенному собственному объему 1 моль газа. В 1 моль газа находится 6,02 102 молекул (Аа=6,02 ■ 1023 моль), следовательно, объем одной молекулы равен nd3l6 = b (4Л\), откуда ^=л/36/(2яАд). Постоянная b=RTip/(&prJ, тогда
t
/ IRT^ I 3.8 31 Дж K-i моль1 . 126 к
d= / = л / — * •
х/ V 16 • 3,14 ■ 3,40 • 106 Па • 6,02 1023 моль"1
Вычисляем на калькуляторе выражение
3 / 3 126 8,31
16 • 3,14 3,40 10б 6,02 1023


по программе
3 0 126 0 8,31 0 16 0 3,14 R13,40 [вп| 6 0
| 6,02 [ВП
Показания индикатора: 3,126—10, т. е. 3,126 • 10 *°.
Так как данное выражение состоит только из произведения и частного, то, согласно правилам округления, его надо округлить до такого числа значащих цифр, которое имеет наименьшее точное исходное данное.
Ответ'. 3,13 • 10“10 м.
-
Определить, сколько ядер в 1 г радиоактивного fgSr распадается в течение одного года.
Дано: /и=10-3 кг; Т—21 лет; f=l год.
Найти: N.
Решение. Для определения числа атомов, содержащихся в 1 г 3gSr, используем соотношение

(1)
N0=vNA = ^NAl
м
где Na — постоянная Авогадро; v — число молей, содержащихся в массе данного элемента; Л/ — молярная масса изотопа. Между молярной массой изотопа и его относительной массой существует соотношение


М = 10 3 А кг/моль.
(2)
Для всякого изотопа относительная атомная масса весьма близка к его массовому числу Л, т. е. для данного случая М—103 • 90 кг/моль=9 ’ 10 2 кг/моль.
Используя закон радиоактивного распада

13)
#=#оехр(-2/),
где Nq — начальное число нераспавшихся ядер в момент /=0; N — число нераспавшихся ядер в момент /; 2 — постоянная радиоактивного распада, определим количество распавшихся ядер з8 Sr в течение 1 года:

(4)
N'=NO-N=NO[1 —exp (—2/)].
Учитывая, что постоянная радиоактивного распада связана с периодом полураспада соотношением 2=1п2/Г, получаем
 (5)
(5)







Подставляя (1) с учетом (2) в выражение (5), имеем 1п2 V
1 — exp
10
3 А
Произведя вычисления по формуле (6), найдем
__ 10
3 кг
#= X
10 3 90 кг/моль
1п2
27 лет
x 6,02 1023 моль
1 —exp
• 1 год .
(6)


10’3
• 6,02 • 1023
10
3 90
1—exp
Вычислим на калькуляторе выражение 1п2 '
— • 1 27
по программе

x 6,02 ВП
2 In[х] 1[7] 27[3(ZE3 F е* I*-4111
Показания индикатора: 1,69532 20, т. е. 1,69532 1О20.
Ответ: 1,70 Ю20.
ФУНДАМЕНТАЛЬНЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ*
Гравитационная постоянная — коэффициент пропорциональности, входящий в закон тяготения Ньютона:
F= Gmxm2lr2,
где F — сила притяжения двух материальных точек массами тх и т2, находящихся на расстоянии г.
Постоянная Авогадро определяет число структурных элементов (атомов, молекул, ионов или других частиц) в единице количества вещества (в одном моле). Названа в честь итальянского ученого А. Авогадро.
Универсальная (молярная) газовая постоянная, входящая в уравнение состояния одного моля идеального газа: pVm=RT, где р — давление газа, Ут — молярный объем газа, Т — термодинамическая температура газа. Физический смысл газовой постоянной — это работа расширения одного моля идеального газа под постоянным давлением при нагревании на 1 К. С другой сторо-
•Значения некоторых фундаментальных физических постоянных приведены в Приложении 1.
ны, газовая постоянная — разность молярных теплоемкостей при постоянном давлении и при постоянном объеме Ср — Cv—R.
Постоянная Больцмана равна отношению молярной газовой постоянной к постоянной Авогадро: k=R/NA.
Постоянная Больцмана входит в ряд важнейших соотношений физики: в уравнение состояния идеального газа, в выражение для средней энергии теплового движения частиц, связывает энтропию физической системы с ее термодинамической вероятностью. Названа в честь австрийского физика Л. Больцмана.
Молярный объем идеального газа, т. е. объем, приходящийся на количество вещества газа 1 моль при нормальных условиях (р0= 101,325 кПа, Т0=273,12 К), определяется из соотношения
Vm=RTq/p0.
Элементарный электрический заряд (е), наименьший электрический заряд, положительный или отрицательный, равный по значению заряду электрона. Почти все элементарные частицы обладают электрическим зарядом +е или — е или являются незаряженными.
Постоянная Фарадея — равна произведению постоянной Авогадро на элементарный электрический заряд (заряд электрона) F—NAe. Названа в честь английского физика М. Фарадея.
Скорость света в вакууме (скорость распространения любых электромагнитных волн) представляет собой предельную скорость распространения любых физических воздействий, инварианта при переходе от одной системы отсчета к другим.
Постоянная Стефана — Больцмана входит в закон, определяющий полную (по всем длинам волн) испускательную способность черного тела: R = aT4\ где R — испускательная способность черного тела, Т — термодинамическая температура. Закон сформулирован на основании экспериментальных данных австрийским физиком И. Стефаном (1879), теоретически получен австрийским физиком Л. Больцманом (1884).
Постоянная Вина входит в закон смещения Вина, утверждающий, что длина на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна термодинамической температуре Т излучающего тела:
Постоянная Планка (квант действия) определяет широкий круг физических явлений, для которых существенна дискретность величин с размерностью действия. Введена в 1900 г. немецким физиком М. Планком при установлении закона распределения энергии в спектре излучения черного тела.
Постоянная Ридберга входит в выражения для уровней энер
гии и частот излучения атомов (спектральные серии): /1 Л
v=7< I ——- ), где nt и пк — числа, определяющие начальный \п: nJ
и конечный уровни энергии. Для каждой спектральной серии nt постоянно, а лЛ=л,+ 1, и,+2, ... . Введена шведским физиком И. Р. Ридбергом.
Радиус первой воровской орбиты (в теории датского физика Н. Бора) — радиус ближайшей к ядру (протону) электронной орбиты. В квантовой механике определяется как расстояние от ядра, на котором с наибольшей вероятностью можно обнаружить электрон в невозбужденном атоме водорода.
Комптоновская длина волны определяет изменение длины волны электромагнитного излучения при комптоновском рассеянии
1 Л / ГТ
на электроне —, где h — постоянная Планка, те — масса покоя электрона, с — скорость света в вакууме. Эффект открыт американским физиком А. Комптоном (1892).
Атомная единица массы применяется в атомной и ядерной физике для выражения масс элементарных частиц атомов и молекул; 1 а. е. м. равна 1/12 массы нуклида углерода 12С.
Электрическая и магнитная постоянные — физические посто- v 1 янные, входящие в формулы электромагнетизма: £0/20=—, где с1
с — скорость света в вакууме.
УЧЕБНЫЕ МАТЕРИАЛЫ ПО РАЗДЕЛАМ КУРСА
ФИЗИКИ
1 2 3 4 5 6 7 8 9 ... 12
СОВРЕМЕННАЯ ФИЗИЧЕСКАЯ КАРТИНА МИРА
Вещество и поле. Атомно-молекулярное строение вещества. Атомное ядро. Кварки. Элементарные частицы, лептоны, адроны. Взаимопревращения частиц. Сильное, электромагнитное, слабое и гравитационное взаимодействия. Иерархия взаимодействий. О единых теориях материи. Физическая картина мира как философская категория.
ПРИМЕНЕНИЕ МИКРОКАЛЬКУЛЯТОРА
ПРИ РЕШЕНИИ ЗАДАЧ
Важнейшим средством совершенного научного исследования является математическое моделирование физических явлений и исследование этих моделей с помощью ЭВМ. Совершенные ЭВМ позволяют проводить сложнейшие расчеты. В некоторых областях науки, например астрофизике, проведение реальных экспериментов практически невозможно, поэтому исследователями проводится вычислительный эксперимент. ЭВМ нужны не только для проведения машинного эксперимента, но и для обработки результатов реальных экспериментов. Совершенный фи- 20
зический эксперимент часто дает столько информации, что обработать ее без ЭВМ практически невозможно.
Для решения любой задачи необходим алгоритм. Под алгоритмом понимают понятное и точное предписание ЭВМ совершать последовательность действий для достижения указанной цели или решения конкретной задачи. Всякий алгоритм строится в расчете на конкретного исполнителя. Таким исполнителем для проведения инженерных и студенческих расчетов различного вида заданий являются микрокалькуляторы семейства «Электроника». Это электронно-вычислительное устройство миниатюрных размеров индивидуального пользования. Оно может быть успешно использовано при решении задач, предлагаемых в контрольных работах. Выполняя вычисления с помощью микрокалькулятора, вы экономите время, освобождая его для изучения теоретических основ курса физики.
Прежде чем пользоваться микрокалькулятором, внимательно ознакомьтесь с руководством по эксплуатации:
-
изучите общие сведения об устройстве;
-
ознакомьтесь с правилами подготовки его к работе.
Рассмотрим решение следующих задач с применением микрокалькулятора.
-
Вычислить эффективный диаметр молекул азота, если его критическая температура 126 К, критическое давление 3,40 МПа.
Дано: 7^=126 К; ^ = 3,40 106 Па.
Найти: d.
Решение. Азот, согласно условию задачи, должен подчиняться уравнению Ван-дер-Ваальса:
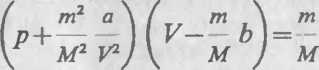
Постоянную b в уравнении Ван-дер-Ваальса с достаточной степенью точности считают равной учетверенному собственному объему 1 моль газа. В 1 моль газа находится 6,02 102 молекул (Аа=6,02 ■ 1023 моль), следовательно, объем одной молекулы равен nd3l6 = b (4Л\), откуда ^=л/36/(2яАд). Постоянная b=RTip/(&prJ, тогда
t
/ IRT^ I 3.8 31 Дж K-i моль1 . 126 к
d= / = л / — * •
х/ V 16 • 3,14 ■ 3,40 • 106 Па • 6,02 1023 моль"1
Вычисляем на калькуляторе выражение
3 / 3 126 8,31
16 • 3,14 3,40 10б 6,02 1023


по программе
3 0 126 0 8,31 0 16 0 3,14 R13,40 [вп| 6 0
| 6,02 [ВП
Показания индикатора: 3,126—10, т. е. 3,126 • 10 *°.
Так как данное выражение состоит только из произведения и частного, то, согласно правилам округления, его надо округлить до такого числа значащих цифр, которое имеет наименьшее точное исходное данное.
Ответ'. 3,13 • 10“10 м.
-
Определить, сколько ядер в 1 г радиоактивного fgSr распадается в течение одного года.
Дано: /и=10-3 кг; Т—21 лет; f=l год.
Найти: N.
Решение. Для определения числа атомов, содержащихся в 1 г 3gSr, используем соотношение

(1)
N0=vNA = ^NAl
м
где Na — постоянная Авогадро; v — число молей, содержащихся в массе данного элемента; Л/ — молярная масса изотопа. Между молярной массой изотопа и его относительной массой существует соотношение


М = 10 3 А кг/моль.
(2)
Для всякого изотопа относительная атомная масса весьма близка к его массовому числу Л, т. е. для данного случая М—103 • 90 кг/моль=9 ’ 10 2 кг/моль.
Используя закон радиоактивного распада

13)
#=#оехр(-2/),
где Nq — начальное число нераспавшихся ядер в момент /=0; N — число нераспавшихся ядер в момент /; 2 — постоянная радиоактивного распада, определим количество распавшихся ядер з8 Sr в течение 1 года:

(4)
N'=NO-N=NO[1 —exp (—2/)].
Учитывая, что постоянная радиоактивного распада связана с периодом полураспада соотношением 2=1п2/Г, получаем
 (5)
(5)







Подставляя (1) с учетом (2) в выражение (5), имеем 1п2 V
1 — exp
10
3 А
Произведя вычисления по формуле (6), найдем
__ 10
3 кг
СОВРЕМЕННАЯ ФИЗИЧЕСКАЯ КАРТИНА МИРА
Вещество и поле. Атомно-молекулярное строение вещества. Атомное ядро. Кварки. Элементарные частицы, лептоны, адроны. Взаимопревращения частиц. Сильное, электромагнитное, слабое и гравитационное взаимодействия. Иерархия взаимодействий. О единых теориях материи. Физическая картина мира как философская категория.
ПРИМЕНЕНИЕ МИКРОКАЛЬКУЛЯТОРА
ПРИ РЕШЕНИИ ЗАДАЧ
Важнейшим средством совершенного научного исследования является математическое моделирование физических явлений и исследование этих моделей с помощью ЭВМ. Совершенные ЭВМ позволяют проводить сложнейшие расчеты. В некоторых областях науки, например астрофизике, проведение реальных экспериментов практически невозможно, поэтому исследователями проводится вычислительный эксперимент. ЭВМ нужны не только для проведения машинного эксперимента, но и для обработки результатов реальных экспериментов. Совершенный фи- 20
зический эксперимент часто дает столько информации, что обработать ее без ЭВМ практически невозможно.
Для решения любой задачи необходим алгоритм. Под алгоритмом понимают понятное и точное предписание ЭВМ совершать последовательность действий для достижения указанной цели или решения конкретной задачи. Всякий алгоритм строится в расчете на конкретного исполнителя. Таким исполнителем для проведения инженерных и студенческих расчетов различного вида заданий являются микрокалькуляторы семейства «Электроника». Это электронно-вычислительное устройство миниатюрных размеров индивидуального пользования. Оно может быть успешно использовано при решении задач, предлагаемых в контрольных работах. Выполняя вычисления с помощью микрокалькулятора, вы экономите время, освобождая его для изучения теоретических основ курса физики.
Прежде чем пользоваться микрокалькулятором, внимательно ознакомьтесь с руководством по эксплуатации:
-
изучите общие сведения об устройстве;
-
ознакомьтесь с правилами подготовки его к работе.
Рассмотрим решение следующих задач с применением микрокалькулятора.
-
Вычислить эффективный диаметр молекул азота, если его критическая температура 126 К, критическое давление 3,40 МПа.
Дано: 7^=126 К; ^ = 3,40 106 Па.
Найти: d.
Решение. Азот, согласно условию задачи, должен подчиняться уравнению Ван-дер-Ваальса:
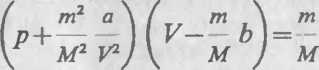
Постоянную b в уравнении Ван-дер-Ваальса с достаточной степенью точности считают равной учетверенному собственному объему 1 моль газа. В 1 моль газа находится 6,02 102 молекул (Аа=6,02 ■ 1023 моль), следовательно, объем одной молекулы равен nd3l6 = b (4Л\), откуда ^=л/36/(2яАд). Постоянная b=RTip/(&prJ, тогда
t
/ IRT^ I 3.8 31 Дж K-i моль1 . 126 к
d= / = л / — * •
х/ V 16 • 3,14 ■ 3,40 • 106 Па • 6,02 1023 моль"1
Вычисляем на калькуляторе выражение
3 / 3 126 8,31
16 • 3,14 3,40 10б 6,02 1023


по программе
3 0 126 0 8,31 0 16 0 3,14 R13,40 [вп| 6 0
| 6,02 [ВПизучите общие сведения об устройстве;
ознакомьтесь с правилами подготовки его к работе.
Вычислить эффективный диаметр молекул азота, если его критическая температура 126 К, критическое давление 3,40 МПа.
Показания индикатора: 3,126—10, т. е. 3,126 • 10 *°.
Так как данное выражение состоит только из произведения и частного, то, согласно правилам округления, его надо округлить до такого числа значащих цифр, которое имеет наименьшее точное исходное данное.
Ответ'. 3,13 • 10“10 м.
-
Определить, сколько ядер в 1 г радиоактивного fgSr распадается в течение одного года.
Дано: /и=10-3 кг; Т—21 лет; f=l год.
Найти: N.
Решение. Для определения числа атомов, содержащихся в 1 г 3gSr, используем соотношение

(1)
N0=vNA = ^NAl
м
где Na — постоянная Авогадро; v — число молей, содержащихся в массе данного элемента; Л/ — молярная масса изотопа. Между молярной массой изотопа и его относительной массой существует соотношение


М = 10 3 А кг/моль.
(2)
Для всякого изотопа относительная атомная масса весьма близка к его массовому числу Л, т. е. для данного случая М—103 • 90 кг/моль=9 ’ 10 2 кг/моль.
Используя закон радиоактивного распада

13)
#=#оехр(-2/),
где Nq — начальное число нераспавшихся ядер в момент /=0; N — число нераспавшихся ядер в момент /; 2 — постоянная радиоактивного распада, определим количество распавшихся ядер з8 Sr в течение 1 года:

(4)
N'=NO-N=NO[1 —exp (—2/)].
Учитывая, что постоянная радиоактивного распада связана с периодом полураспада соотношением 2=1п2/Г, получаем







Подставляя (1) с учетом (2) в выражение (5), имеем 1п2 V
1 — exp
10
#= X
10 3 90 кг/моль
1п2
27 лет
x 6,02 1023 моль
1 —exp
• 1 год .
(6)


10’3
• 6,02 • 1023
10
ны, газовая постоянная — разность молярных теплоемкостей при постоянном давлении и при постоянном объеме Ср — Cv—R.
Постоянная Больцмана равна отношению молярной газовой постоянной к постоянной Авогадро: k=R/NA.
Постоянная Больцмана входит в ряд важнейших соотношений физики: в уравнение состояния идеального газа, в выражение для средней энергии теплового движения частиц, связывает энтропию физической системы с ее термодинамической вероятностью. Названа в честь австрийского физика Л. Больцмана.
Молярный объем идеального газа, т. е. объем, приходящийся на количество вещества газа 1 моль при нормальных условиях (р0= 101,325 кПа, Т0=273,12 К), определяется из соотношения
Vm=RTq/p0.
Элементарный электрический заряд (е), наименьший электрический заряд, положительный или отрицательный, равный по значению заряду электрона. Почти все элементарные частицы обладают электрическим зарядом +е или — е или являются незаряженными.
Постоянная Фарадея — равна произведению постоянной Авогадро на элементарный электрический заряд (заряд электрона) F—NAe. Названа в честь английского физика М. Фарадея.
Скорость света в вакууме (скорость распространения любых электромагнитных волн) представляет собой предельную скорость распространения любых физических воздействий, инварианта при переходе от одной системы отсчета к другим.
Постоянная Стефана — Больцмана входит в закон, определяющий полную (по всем длинам волн) испускательную способность черного тела: R = aT4\ где R — испускательная способность черного тела, Т — термодинамическая температура. Закон сформулирован на основании экспериментальных данных австрийским физиком И. Стефаном (1879), теоретически получен австрийским физиком Л. Больцманом (1884).
Постоянная Вина входит в закон смещения Вина, утверждающий, что длина на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна термодинамической температуре Т излучающего тела:
Постоянная Планка (квант действия) определяет широкий круг физических явлений, для которых существенна дискретность величин с размерностью действия. Введена в 1900 г. немецким физиком М. Планком при установлении закона распределения энергии в спектре излучения черного тела.
Постоянная Ридберга входит в выражения для уровней энер
I. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ,
МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
Пояснения к рабочей программе
Приступая к изучению физики, необходимо уяснить, что физика, наряду с другими естественными науками, изучает объективные свойства окружающего нас материального мира. Она исследует наиболее общие формы движения материи и их взаимные превращения. Движение есть форма существования материи. Физические понятия являются простейшими и в то же время основополагающими и всеобщими в естествознании (пространство, время, движение, масса, работа, энергия и др.).
Изучать основы классической механики надо исходя из представлений современной физики, в которой основные понятия классической механики не утратили своего значения, а получили дальнейшее развитие, обобщение и критическую оценку с точки зрения их применения. Следует помнить, что механика — это наука о простейших формах движения материальных тел и происходящих при этом взаимодействиях между телами. Движение всегда существует в пространстве и во времени. Диалектический материализм учит, что пространство и время являются основными формами существования материи. Предметом классической механики является движение макроскопических материальных тел, совершаемое со скоростями, малыми по сравнению со скоростью света в вакууме. Движение частиц со скоростями порядка скорости света рассматривается в теории относительности, а движение микрочастиц изучается в квантовой механике.
В контрольную работу № 1 включены задачи, дающие возможность проверить знания студентов по ключевым вопросам классической механики и элементам специальной теории относительности. Решая задачи по кинематике, в которых необходимо использовать математический аппарат дифференциального и интегрального исчисления, студент должен научиться определять мгновенные скорость и ускорение по заданной зависимости координаты от времени и решать обратные задачи.
Задачи на динамику материальной точки и поступательного движения твердого тела охватывают такие вопросы, как закон движения центра масс механической системы, закон сохранения количества движения, работа силы и ее выражение через криволинейный интеграл, связь кинетической энергии механической системы с работой сил, приложенных к этой системе, закон сохранения механической энергии. Тщательного изучения и понимания требуют вопросы о поле как форме материи, осуществляющей взаимодействие между частицами вещества или телами, о потенциальной энергии механической системы.