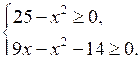ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 126
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
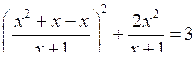 ;
;
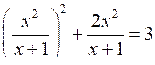 .
.
С д е л а е м з а м е н у: = t. Получим:
t2 + 2t – 3 = 0;
t1 = 1, t2 = –3.
В е р н е м с я к з а м е н е:
О т в е т: .
V. Проверочная работа.
В а р и а н т 1
Решите уравнение:
а)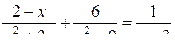 ;
;
б)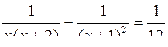 .
.
В а р и а н т 2
Решите уравнение:
а) ;
б)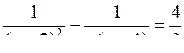 .
.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какими приемами и методами можно решать дробно-рациональные уравнения?
– Опишите решение дробно-рационального уравнения по алгоритму.
– В каких случаях при решении дробно-рациональных уравнений целесообразно использовать метод введения новой переменной?
Домашнее задание: № 296 (б), № 294 (б), № 297 (в), № 298 (б).
Д о п о л н и т е л ь н о: № 299 (б).
У р о к 30 Дата:
АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ
ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Цели: ввести понятие неравенства второй степени с одной переменной и изучить алгоритм решения таких неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Определите количество корней уравнения ах2 + bx + c = 0 и знак коэффициента а, если на рисунке изображен график функции
у = ах2 +
+ bx + c.
а)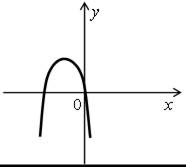 б)
б) 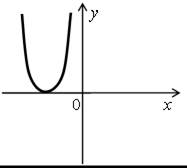
в)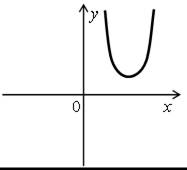
2. Назовите промежутки знакопостоянства функции у = ах2 + bx + c, если ее график изображен на рисунке:
а)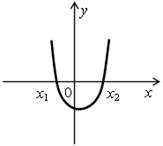 б)
б) 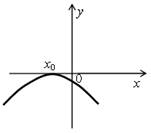
в)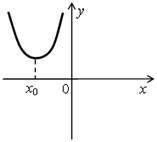
III. Объяснение нового материала.
1. В в е д е н и е п о н я т и я неравенства второй степени с одной переменной.
З а д а н и е. Какие из следующих неравенств являются неравенствами второй степени с одной переменной?
а) 2х2 + 3х – 1 > 0; г) 2х2 – х + 1 < х4;
б) 4х2 – х ≤ 0; д) х2 ≥ 1;
в) 5х – 1 > 3х2; е) х2 – 4x < .
2. С о с т а в л е н и е а л г о р и т м а решения неравенств второй степени с одной переменной.
Поставить перед учащимися проблему: как может быть решено неравенство подобного вида? Если учащиеся не догадаются, то можно вернуться к заданиям устной работы и наводящими вопросами помочь им сделать в ы в о д: неравенства второй степени с одной переменной решаются графически.
Желательно, чтобы учащиеся самостоятельно вывели алгоритм решения этих неравенств.
3. Р а с с м о т р е н и е п р и м е р о в решения неравенств второй степени с одной переменной.
IV. Формирование умений и навыков.
На этом уроке необходимо рассмотреть разные ситуации, возникающие при решении неравенств второй степени с одной переменной. Нужно, чтобы учащиеся запомнили алгоритм и применяли его без помощи учителя.
В соответствии с количеством корней трехчлена, получаемых в процессе решения неравенств, все задания можно разбить на три группы. В первую группу войдут неравенства, у которых квадратный трехчлен имеет два корня
, во вторую – один корень, и в третьей группе будут неравенства, квадратный трехчлен которых не имеет корней.
Упражнения:
1-я г р у п п а.
№ 304 (а, в, ж), № 308 (а, в, д).
2-я г р у п п а.
1. № 304 (д).
2. 9х2 + 6х + 1 ≤ 0
3-я г р у п п а.
а) х2 + 2х + 4 > 0;
б) 2х2 – х + 3 ≤ 0;
в) –х2 + 3х – 7 < 0.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие неравенства называются неравенствами второй степени с одной переменной?
– Опишите алгоритм решения неравенств второй степени с одной переменной.
– Какие решения может иметь неравенство второй степени с одной переменной, если соответствующий квадратный трехчлен не имеет корней?
Домашнее задание: № 304 (б, г, е, з), № 306 (б, в), № 308 (б, г).
У р о к 31 Дата:
ПРИМЕНЕНИЕ АЛГОРИТМА РЕШЕНИЯ НЕРАВЕНСТВ
ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Цели: продолжить формирование умения решать неравенства второй степени с одной переменной.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите неравенства ах2 + bx + c > 0 и ах2 + bx + c ≤ 0, если на рисунке изображен график соответствующей квадратичной функции:
а)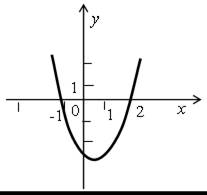 б)
б) 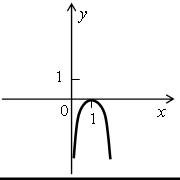
в)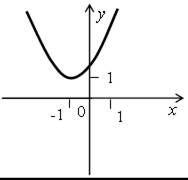
III. Формирование умений и навыков.
Упражнения:
1. № 307, № 309 (а, в, д).
2. № 312 (а, в).
3. № 315 (а, в, е), № 316.
IV. Математический диктант.
«+» – согласен с утверждением; «–» – не согласен с утверждением.
1) Неравенства второй степени с одной переменной решаются с помощью графика квадратичной функции.
2) Для решения неравенств второй степени с одной переменной нужно знать координату вершины соответствующей параболы.
3) Для решения неравенств второй степени с одной переменной достаточно знать направление ветвей соответствующей параболы.
4) Если квадратный трехчлен имеет корни, то соответствующее неравенство обязательно имеет решения.
5) Если квадратный трехчлен не имеет корней, то соответствующее неравенство не имеет решений.
6) Если вершина параболы лежит на оси абсцисс, то соответствующее неравенство не имеет решений.
7) Неравенства второй степени с одной переменной может иметь решение, состоящее из единственного числа.
8) Решением неравенства второй степени с одной переменной может быть множество всех чисел.
9) Если а < 0, х1 и х2 – корни квадратного трехчлена ах2 + bx + c, то решением неравенства ах2 + bx + c > 0 будет промежуток (–∞; х1) (х2; +∞).
10) Если а > 0 и х0 – единственный корень квадратного трехчлена ах2 + bx + c, то решением неравенства ах2 + bx + c > 0 будет промежуток (–∞; х0) (х0; +∞).
К л ю ч: + – – + – – + + – +.
V. Итоги урока.
Учащиеся обмениваются тетрадями, учитель вновь зачитывает вопросы математического диктанта. Происходит обсуждение ответов и учащиеся выставляют друг другу оценки по следующей шкале:
«5» – не менее 9 правильных ответов;
«4» – 7, 8 правильных ответов;
«3» – 5, 6 правильных ответов;
«2» – менее 5 правильных ответов.
Домашнее задание: № 309 (г, е), № 313, № 317.
У р о к 32 Дата:
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ, ТРЕБУЮЩИЕ ПРИМЕНЕНИЯ
АЛГОРИТМА РЕШЕНИЯ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ
С ОДНОЙ ПЕРЕМЕННОЙ
Цели: продолжить формирование умения применять алгоритм решения неравенств второй степени с одной переменной.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите неравенство ах2 + bx + c ≤ 0 и ах2 + bx + c > 0, если на рисунке изображен график соответствующей квадратичной функции:
а)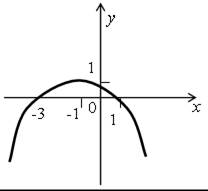 б)
б) 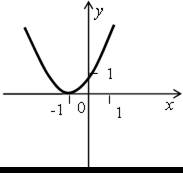
в)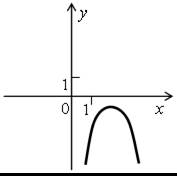
III. Проверочная работа.
В а р и а н т 1
Решите неравенство:
а) х2 – 8х + 15 > 0; в) 4х2 + 4х + 1 ≤ 0;
б) 2х – х2 ≥ 0; г) х2 + 2х + 3 > 0.
В а р и а н т 2
Решите неравенство:
а) х2 – 10х + 21 ≤ 0; в) х2 – 10х + 25 > 0;
б) 9 – х2 < 0; г) –х2 + х – 4 ≤ 0.
IV. Формирование умений и навыков.
На этом уроке учащиеся должны решать более сложные задания, которые потребуют от них осознанного владения алгоритмом решения неравенств второй степени с одной переменной.
Все задания можно разбить на 2 группы. Если класс невысокого уровня подготовки, то вторую группу заданий решать не нужно. Кроме того, сильным в учебе учащимся можно дать дополнительные задания на решение уравнений и неравенств с параметрами.
Упражнения:
1-я г р у п п а.
1. № 310 (а), № 311 (а).
2. № 314 (а).
3.№ 318.
Р е ш е н и е
Пусть одна сторона прямоугольника равна а см, тогда другая сторона равна (а + 7) см. Значит, площадь прямоугольника равна а (а + 7) см2, а по условию она не превосходит 60 см2. Получим неравенство:
а (а + 7) ≤ 60;
а (а + 7) – 60 ≤ 0.
Решая его, находим, что а [–12; 5], то есть меньшая сторона прямоугольника не должна превосходить 5 см.
О т в е т: не превосходит 5 см.
2-я г р у п п а.
1. № 320 (а, в, д).
Р е ш е н и е
а)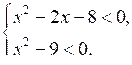
Найдем корни квадратных трехчленов и изобразим схематически параболы на одной числовой прямой:
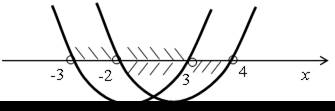
По рисунку видим, что решением данной системы будет промежуток (–2; 3).
О т в е т: (–2; 3).
2. № 321 (а).
Р е ш е н и е
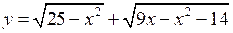
Для нахождения области определения данной функции достаточно решить систему неравенств:
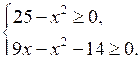
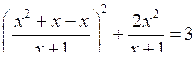 ;
;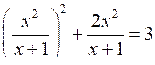 .
.С д е л а е м з а м е н у: = t. Получим:
t2 + 2t – 3 = 0;
t1 = 1, t2 = –3.
В е р н е м с я к з а м е н е:
| = 1; или х2 – х – 1 = 0; D = 1 + 4 = 5; х1, 2 = . | = –3; х2 + 3х + 3 = 0; D = 9 – 12 = –3. Решений нет. |
О т в е т: .
V. Проверочная работа.
В а р и а н т 1
Решите уравнение:
а)
б)
В а р и а н т 2
Решите уравнение:
а) ;
б)
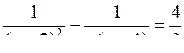 .
.VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какими приемами и методами можно решать дробно-рациональные уравнения?
– Опишите решение дробно-рационального уравнения по алгоритму.
– В каких случаях при решении дробно-рациональных уравнений целесообразно использовать метод введения новой переменной?
Домашнее задание: № 296 (б), № 294 (б), № 297 (в), № 298 (б).
Д о п о л н и т е л ь н о: № 299 (б).
У р о к 30 Дата:
АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ
ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Цели: ввести понятие неравенства второй степени с одной переменной и изучить алгоритм решения таких неравенств.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Определите количество корней уравнения ах2 + bx + c = 0 и знак коэффициента а, если на рисунке изображен график функции
у = ах2 +
+ bx + c.
а)
 б)
б) 
в)

2. Назовите промежутки знакопостоянства функции у = ах2 + bx + c, если ее график изображен на рисунке:
а)
 б)
б) 
в)

III. Объяснение нового материала.
1. В в е д е н и е п о н я т и я неравенства второй степени с одной переменной.
З а д а н и е. Какие из следующих неравенств являются неравенствами второй степени с одной переменной?
а) 2х2 + 3х – 1 > 0; г) 2х2 – х + 1 < х4;
б) 4х2 – х ≤ 0; д) х2 ≥ 1;
в) 5х – 1 > 3х2; е) х2 – 4x < .
2. С о с т а в л е н и е а л г о р и т м а решения неравенств второй степени с одной переменной.
Поставить перед учащимися проблему: как может быть решено неравенство подобного вида? Если учащиеся не догадаются, то можно вернуться к заданиям устной работы и наводящими вопросами помочь им сделать в ы в о д: неравенства второй степени с одной переменной решаются графически.
Желательно, чтобы учащиеся самостоятельно вывели алгоритм решения этих неравенств.
3. Р а с с м о т р е н и е п р и м е р о в решения неравенств второй степени с одной переменной.
IV. Формирование умений и навыков.
На этом уроке необходимо рассмотреть разные ситуации, возникающие при решении неравенств второй степени с одной переменной. Нужно, чтобы учащиеся запомнили алгоритм и применяли его без помощи учителя.
В соответствии с количеством корней трехчлена, получаемых в процессе решения неравенств, все задания можно разбить на три группы. В первую группу войдут неравенства, у которых квадратный трехчлен имеет два корня
, во вторую – один корень, и в третьей группе будут неравенства, квадратный трехчлен которых не имеет корней.
Упражнения:
1-я г р у п п а.
№ 304 (а, в, ж), № 308 (а, в, д).
2-я г р у п п а.
1. № 304 (д).
2. 9х2 + 6х + 1 ≤ 0
3-я г р у п п а.
а) х2 + 2х + 4 > 0;
б) 2х2 – х + 3 ≤ 0;
в) –х2 + 3х – 7 < 0.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие неравенства называются неравенствами второй степени с одной переменной?
– Опишите алгоритм решения неравенств второй степени с одной переменной.
– Какие решения может иметь неравенство второй степени с одной переменной, если соответствующий квадратный трехчлен не имеет корней?
Домашнее задание: № 304 (б, г, е, з), № 306 (б, в), № 308 (б, г).
У р о к 31 Дата:
ПРИМЕНЕНИЕ АЛГОРИТМА РЕШЕНИЯ НЕРАВЕНСТВ
ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
Цели: продолжить формирование умения решать неравенства второй степени с одной переменной.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите неравенства ах2 + bx + c > 0 и ах2 + bx + c ≤ 0, если на рисунке изображен график соответствующей квадратичной функции:
а)
 б)
б) 
в)

III. Формирование умений и навыков.
Упражнения:
1. № 307, № 309 (а, в, д).
2. № 312 (а, в).
3. № 315 (а, в, е), № 316.
IV. Математический диктант.
«+» – согласен с утверждением; «–» – не согласен с утверждением.
1) Неравенства второй степени с одной переменной решаются с помощью графика квадратичной функции.
2) Для решения неравенств второй степени с одной переменной нужно знать координату вершины соответствующей параболы.
3) Для решения неравенств второй степени с одной переменной достаточно знать направление ветвей соответствующей параболы.
4) Если квадратный трехчлен имеет корни, то соответствующее неравенство обязательно имеет решения.
5) Если квадратный трехчлен не имеет корней, то соответствующее неравенство не имеет решений.
6) Если вершина параболы лежит на оси абсцисс, то соответствующее неравенство не имеет решений.
7) Неравенства второй степени с одной переменной может иметь решение, состоящее из единственного числа.
8) Решением неравенства второй степени с одной переменной может быть множество всех чисел.
9) Если а < 0, х1 и х2 – корни квадратного трехчлена ах2 + bx + c, то решением неравенства ах2 + bx + c > 0 будет промежуток (–∞; х1) (х2; +∞).
10) Если а > 0 и х0 – единственный корень квадратного трехчлена ах2 + bx + c, то решением неравенства ах2 + bx + c > 0 будет промежуток (–∞; х0) (х0; +∞).
К л ю ч: + – – + – – + + – +.
V. Итоги урока.
Учащиеся обмениваются тетрадями, учитель вновь зачитывает вопросы математического диктанта. Происходит обсуждение ответов и учащиеся выставляют друг другу оценки по следующей шкале:
«5» – не менее 9 правильных ответов;
«4» – 7, 8 правильных ответов;
«3» – 5, 6 правильных ответов;
«2» – менее 5 правильных ответов.
Домашнее задание: № 309 (г, е), № 313, № 317.
У р о к 32 Дата:
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ, ТРЕБУЮЩИЕ ПРИМЕНЕНИЯ
АЛГОРИТМА РЕШЕНИЯ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ
С ОДНОЙ ПЕРЕМЕННОЙ
Цели: продолжить формирование умения применять алгоритм решения неравенств второй степени с одной переменной.
Ход урока
I. Организационный момент.
II. Устная работа.
Решите неравенство ах2 + bx + c ≤ 0 и ах2 + bx + c > 0, если на рисунке изображен график соответствующей квадратичной функции:
а)
 б)
б) 
в)

III. Проверочная работа.
В а р и а н т 1
Решите неравенство:
а) х2 – 8х + 15 > 0; в) 4х2 + 4х + 1 ≤ 0;
б) 2х – х2 ≥ 0; г) х2 + 2х + 3 > 0.
В а р и а н т 2
Решите неравенство:
а) х2 – 10х + 21 ≤ 0; в) х2 – 10х + 25 > 0;
б) 9 – х2 < 0; г) –х2 + х – 4 ≤ 0.
IV. Формирование умений и навыков.
На этом уроке учащиеся должны решать более сложные задания, которые потребуют от них осознанного владения алгоритмом решения неравенств второй степени с одной переменной.
Все задания можно разбить на 2 группы. Если класс невысокого уровня подготовки, то вторую группу заданий решать не нужно. Кроме того, сильным в учебе учащимся можно дать дополнительные задания на решение уравнений и неравенств с параметрами.
Упражнения:
1-я г р у п п а.
1. № 310 (а), № 311 (а).
2. № 314 (а).
3.№ 318.
Р е ш е н и е
Пусть одна сторона прямоугольника равна а см, тогда другая сторона равна (а + 7) см. Значит, площадь прямоугольника равна а (а + 7) см2, а по условию она не превосходит 60 см2. Получим неравенство:
а (а + 7) ≤ 60;
а (а + 7) – 60 ≤ 0.
Решая его, находим, что а [–12; 5], то есть меньшая сторона прямоугольника не должна превосходить 5 см.
О т в е т: не превосходит 5 см.
2-я г р у п п а.
1. № 320 (а, в, д).
Р е ш е н и е
а)
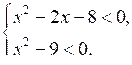
Найдем корни квадратных трехчленов и изобразим схематически параболы на одной числовой прямой:
| х2 – 2х – 8 = 0 х = –2 х = 4 | х2 – 9 = 0 х = –3 х = 3 |

По рисунку видим, что решением данной системы будет промежуток (–2; 3).
О т в е т: (–2; 3).
2. № 321 (а).
Р е ш е н и е
Для нахождения области определения данной функции достаточно решить систему неравенств: