ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1040
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
После введения понятия геометрической вероятности целесообразно дать учащимся под запись правило.
П р а в и л о (нахождения геометрической вероятности).
Пусть фигура F1 содержится в F. Тогда вероятность попадания в фигуру F1, при условии попадания в фигуру F, равна отношению площадей
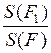.IV. Формирование умений и навыков.
Все задания, которые должны выполнить учащиеся на этом уроке, можно разбить на три группы. В первую группу войдут достаточно простые задания на непосредственное применение понятия геометрической вероятности (желательно заранее на доске заготовить необходимые рисунки). Во вторую группу войдут более сложные задания, в которых учащимся придется применять некоторые дополнительные знания. Задания 3-й группы предназначены для сильных в учебе учащихся.
Упражнения:
1-я г р у п п а.
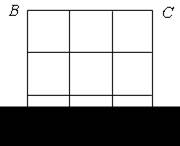
1. На рисунке изображена квадратная мишень ABCD, разбитая на 9 равных квадратиков. Стрелок, не целясь, стреляет в мишень и попадает. Сравните вероятности попадания в правый верхний, центральный и левый квадратики.
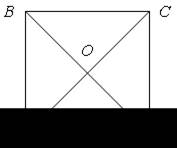
2. На рисунке изображена квадратная мишень ABCD. Стрелок, не целясь, стреляет и попадает в нее. Какова вероятность того, что он попал в треугольник ABC? В треугольник AОB?
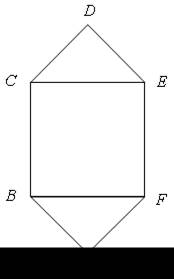
3. На рисунке изображена мишень ABCDEF. Стрелок, не целясь, стреляет в нее и попадает. Какова вероятность того, что он попадет в квадрат BCEF? В равносторонний треугольник BAF? В равносторонний треугольник CDE?
2-я г р у п п а.
№ 814.
Р е ш е н и е
Треугольник CDE гомотетичен треугольнику ABC с коэффициентом гомотетии . Площади гомотетичных фигур относятся друг к другу как k2, где k – коэффициент гомотетии. Вероятность того, что случайным образом выбранная точка попадает в CDE, равна отношению площади CDE к площади ABC, то есть равна
или .
О т в е т: .
№ 815.
Р е ш е н и е
Точка разрыва телефонной линии удалена от точки А не более чем на 500 м. Графически это можно представить так, что точка разрыва находится на отрезке АМ (причем точка разрыва может совпадать и с точкой А и с точкой М). Вероятность того, что точка лежит на отрезке АМ, равна отношению длины отрезка АМ к длине отрезка АВ и равна
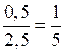= 0,2.О т в е т: 0,2.
П р и м е ч а н и е. Обращаем внимание учащихся на то, что длины отрезков должны выражаться в одинаковых единицах измерения.
3-я г р у п п а.
1. Рассматривается квадратная мишень ABCD. Отметьте на ней две такие фигуры, что:
а) вероятность попадания хотя бы в одну из них, при условии попадания в мишень, равна 1;
б) вероятность попадания в обе фигуры одновременно, при условии попадания в мишень, равна нулю;
в) при условии попадания в мишень вероятность попадания хотя бы в одну фигуру равна 1, а вероятность одновременного попадания в обе фигуры равна .
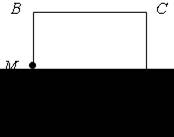
2. На рисунке изображен квадрат ABCD, М – середина стороны AB. Случайным образом выбирают точку Х квадрата и проводят луч СХ. Какова вероятность того, что построенный так луч пересечет отрезок МВ?
V. Самостоятельная работа.
В а р и а н т 1
1. В классе 12 мальчиков, шестерых из них зовут Сережами, четверых – Алешами, а остальных – Сашами. Новый учитель, еще не знающий имен мальчиков, вызывает их к доске.
а) Вызывается один мальчик. Какова вероятность того, что вызванного зовут Сережей?
б) Вызывается один мальчик. Какова вероятность того, что вызванного зовут Алешей?
в) Какое наименьшее количество мальчиков нужно вызвать, чтобы с вероятностью, равной 1, среди них был Саша?
2. Объясните, равновероятны ли следующие события:
а) Сумма цифр наугад написанного двузначного числа равна 1.
б) Сумма цифр наугад написанного двузначного числа равна 5.
В а р и а н т 2
1. В классе 15 девочек, восьмерых из них зовут Ленами, пятерых – Анями, а остальных – Наташами. Новый учитель, еще не знающий имен учащихся, вызывает их к доске.
а) Вызывается одна девочка. Какова вероятность того, что вызванную зовут Наташей?
б) Вызывается одна девочка. Какова вероятность того, что вызванную зовут Леной?
в) Какое наименьшее количество девочек нужно вызвать, чтобы с вероятностью 1 среди них была Аня?
2. Объясните, равновероятны ли следующие события:
а) Сумма цифр наугад написанного трехзначного числа равна 1.
б) Сумма цифр наугад написанного трехзначного числа равна 6.
VI. Итоги урока.
– Какие события называются достоверными? Невозможными? Равновероятными? Приведите примеры.
– В каких ситуациях используется понятие геометрической вероятности?
– Сформулируйте правило нахождения вероятности попадания в фигуру, содержащуюся в другой фигуре.
Домашнее задание.
З а д а ч а. Внутри квадрата со стороной 10 см выделен круг радиусом 2 см. Случайным образом внутри квадрата отмечается точка. Какова вероятность того, что она попадет в выделенный круг?
№ 816, № 859, № 860.
У р о к 83
КОМБИНАТОРНЫЕ МЕТОДЫ РЕШЕНИЯ
ВЕРОЯТНОСТНЫХ ЗАДАЧ
Цель: формировать умения решать задачи на нахождение вероятности случайного события с использованием формул комбинаторики.
Ход урока
I. Организационный момент.
II. Устная работа.
Для каждого из описанных событий определите, каким оно является: невозможным, достоверным или случайным.
а) Из 25 учащихся класса двое справляют день рождения 30 января. (Случайное.)
б) Из 25 учащихся класса двое справляют день рождения 30 февраля. (Невозможное.)
в) Измерены длины сторон треугольника. Оказалось, что длина каждой стороны меньше суммы длин двух других сторон. (Достоверное.)
г) Бросают две игральные кости, сумма выпавших на двух костях очков меньше 15. (Достоверное.)
д) Бросают четыре игральные кости, на всех четырех костях выпало по 3 очка. (Случайное.)
е) На уроке математики ученики решали математические задачи. (Достоверное.)
ж) Из интервала (1; 2) наугад взяли какое-то число, оно оказалось натуральным. (Невозможное.)
III. Проверочная работа.
В а р и а н т 1
На рисунке изображена мишень АВС, имеющая форму равностороннего треугольника; K, М, N – середины его сторон.
| а) Стрелок, стрелявший в мишень не целясь, попал в нее. Какова вероятность, что он попал в четырехугольник АМNK? В треугольник AMK? |  |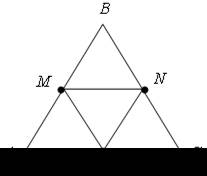
б)* Перерисуйте мишень и заштрихуйте на своем рисунке такую область, что вероятность попадания в нее при случайном попадании в мишень равна .
В а р и а н т 2
На рисунке изображена мишень АВС, имеющая форму равностороннего треугольника; K, М, N – середины его сторон.
| а) Стрелок, стрелявший в мишень не целясь, попал в нее. Какова вероятность, что он попал в четырехугольник KМВN? В треугольник ВMN? |  |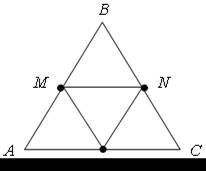
б)* Перерисуйте мишень и заштрихуйте на своем рисунке такую область, что вероятность попадания в нее при случайном попадании в мишень равна .
IV. Актуализация знаний.
Повторение основных комбинаторных формул следует организовать на примере простейших комбинаторных задач, которые может предложить как учитель, так и сами учащиеся. В результате целесообразно составить опорный конспект:
| Комбинации | ||
| Наименование | Существенные отличия | Формула |
| Перестановки из т элементов | Отличаются только порядком выбранных т элементов | Рт = т! |
| Сочетания из п элементов по т | Отличаются только составом входящих в комбинацию т элементов, без учета порядка их расположения |  |
| Размещения из п элементов по т | Отличаются как составом, так и порядком расположения т элементов в комбинации |  |
V. Формирование умений и навыков.
Упражнения:
№ 805.
Р е ш е н и е
Исходы – все возможные перестановки из 5 цифр; общее число исходов п = Р5 = 5! = 120.
Событие А – «после набора цифр сейф откроется», т = 1 (есть только один правильный набор) – число благоприятных исходов.
Р(А) = = .
О т в е т: .
№ 809.
Р е ш е н и е
Исходы – все возможные пары деталей из 10, находящихся в ящике. Общее число исходов n =
= 45 (порядок деталей в паре не учитывается).Событие А – «обе детали оказались стандартными»,
m =
= 36 – число благоприятных исходов.Искомая вероятность: Р(А) = =
= 0,8.О т в е т: 0,8.
№ 858.
Р е ш е н и е
Исходами опыта являются все возможные размещения четырех карточек на трех местах (порядок расположения карточек нам важен). Общее число исходов равно n =
= 2· 3 · 4 = 24.Рассмотрим события и их вероятности:
а) Событие А – «из трех карточек образовано число 123»; т = 1 (единственный вариант) – число благоприятных исходов; Р(А) = = .
б) Событие В – «из трех карточек образовано число 312 или 321»; т = 2 (два варианта размещения) – число благоприятных исходов;
.в) Событие С – «из трех карточек образовано число, первая цифра которого 2». Если цифра фиксирована, то на оставшихся двух местах можно разместить любую из оставшихся трех цифр (с учетом порядка), то есть
– число благоприятных исходов; 
.О т в е т: а) ; б) ; в) .
2. Р е ш е н и е з а д а ч повышенной сложности.
№ 810.
Р е ш е н и е
Исходы – все возможные группы из 4 человек – обладателей билетов на елку – составлены из 27 желающих. Порядок выбора значения не имеет (каждый из четверых получает одинаковый билет). Общее число возможных исходов