ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1045
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В учебнике нет определения понятия «исход случайного события». Можно оперировать таким: исход – возможный результат опыта (эксперимента).
Следует хорошо отличать события от исходов, что в дальнейшем позволит избежать многих трудностей при введении понятия вероятности случайного события.
Далее рассматриваем пример из учебника со с. 188.
И с х о д ы и с п ы т а н и я: 1. Выпадает одно очко.
2. Выпадает два очка.
3. Выпадает три очка.
4. Выпадает четыре очка.
5. Выпадает пять очков.
6. Выпадает шесть очков.
С л у ч а й н о е с о б ы т и е: 1. Выпадет шесть очков.
На этом примере наглядно демонстрируем, что исход испытания – значение наблюдаемого признака (количество очков), непосредственно полученное по окончании эксперимента (каждый эксперимент заканчивается одним и только одним исходом). Событие – появление исхода, обладающего заранее указанным свойством (шесть очков).
Затем вводим понятия «частота события» и «относительная частота события».
В в о д и м ы е о б о з н а ч е н и я:
А – событие;
т – число испытаний, при которых произошло событие А;
п – общее число испытаний;
W(A) = – относительная частота случайного события.
П р о б л е м н ы й в о п р о с: Почему важна относительная частота события? Приведите пример. (Иван попал в мишень три раза, Петр – четыре. Кто из них лучше стреляет? Можно ответить, что Петр – лучше, так как больше число попаданий. Но мы не знаем, сколько у каждого было попыток. Например, Иван сделал всего три выстрела и попал все три раза, относительная частота попадания W(A) = = 1. А Петр сделал серию из 20 выстрелов и попал всего четыре раза: W(A) = = 0,2.)
IV. Формирование умений и навыков.
Упражнения:
№ 787.
Р е ш е н и е
Событие А – появление нестандартной детали;
т = 12 – число нестандартных деталей;
п = 1000 – общее число деталей;
W(A) = =
О т в е т: 0,012.
№ 788.
Р е ш е н и е
Событие А – солнечный день;
т = 46 – число солнечных дней за указанный период;
п = 31 + 31 = 62 – общее число дней в указанном периоде;
W(A) = = = – относительная частота солнечных дней в указанный период времени.
О т в е т: .
При решении первых двух упражнений особое внимание следует уделить грамотной формулировке самого события, возможных исходов испытания, характера испытания, относительной частоты события.
№ 791.
Р е ш е н и е
а) Событие А – появление в тексте буквы «в»;
т = 6 – количество букв «в» в тексте;
п = 164 – общее количество букв в тексте;
W(A) = = ≈ 0,037 – относительная частота появления буквы «в» в тексте.
б) Событие А – появление буквы «м» в тексте;
т = 6 – количество букв в тексте;
п = 164 – общее количество букв в тексте;
W(A) = = ≈ 0,037 – относительная частота появления буквы «м» в тексте.
О т в е т: а) 0,037; б) 0,037.
При выполнении этого упражнения можно обсудить, почему результаты отличаются от данных, приведенных в учебнике (маленький отрывок, только один вид текста – стихотворение, один автор и т. п.).
№ 856 (по вариантам, подсчет не для всех десятков).
а) Событие А – появление простого числа в первом десятке натуральных чисел от 1 до 99;
т = 4 – число простых чисел в первом десятке (2, 3, 5, 7) – частота появления;
п = 10 – количество чисел в первом десятке;
W(A) = = 0,4 – относительная частота события А.
Событие В – появление простого числа в третьем десятке;
т = 2 – число простых чисел в третьем десятке (23, 29) – частота появления;
п = 10 – количество чисел в третьем десятке;
W(B) = = 0,2 – относительная частота события В.
0,4 > 0,2.
б) Событие А – появление простого числа во втором десятке натуральных чисел от 1 до 99;
т = 4 – число простых чисел в втором десятке (11, 13, 17, 19) – частота появления;
п = 10 – количество чисел во втором десятке;
W(A) = = 0,4 – относительная частота события А.
Событие В – появление простого числа в десятом десятке;
т = 1 – число простых чисел в десятом десятке (91) – частота появления;
п = 10 – количество чисел в десятом десятке;
W(B) = = 0,1 – относительная частота события В.
0,4 > 0,1.
О т в е т: а) 0,4 > 0,2; б) 0,4 > 0,1.
V. Итоги урока.
– Что называется случайным событием?
– Что называется исходом эксперимента?
– Что называется относительной частотой случайного события? Приведите примеры.
Домашнее задание: № 789, № 790 (а, в), № 792, № 797 (б, в).
У р о к 80 Дата:
ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ
Цели: ввести понятие вероятности случайного события (статистический подход); формировать умение оценивать вероятность случайного события.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Стрелок делает 20 выстрелов и при этом 17 раз попадает в цель. Определите относительную частоту промахов стрелка. (0,15.)
2. В ящике 36 яблок, из них половина красных, 6 зеленых, а остальные – желтые. Определите относительную частоту появления желтого яблока.
3. У Марины 3 блузки (синяя, голубая, белая) и 4 юбки разных цветов. Она комбинировала блузки и юбки всеми возможными способами. Какова относительная частота надевания синей блузки? (Всего 3 · 4 = 12 комплектов, синяя блузка входит в 4 комплекта, относительная частота .)
III. Объяснение нового материала.
Начинаем с проверки домашнего задания № 792. Суммируем количество опытов по подбрасыванию монеты, проведенных учениками:
N = 50 · n, где п – число учеников в классе. Затем определяем общее число выпадений орла: М = т1 + т2 + … + тп, где тп – число выпадений орла у п-го ученика. И вычисляем относительную частоту выпадения орла при бросании монеты .
Замечаем, что при большом количестве бросков орел выпадает примерно в половине случаев. Значит, результат бросания монеты обладает некоторой закономерностью, хотя итог каждого броска заранее неизвестен.
Числовая оценка шансов на успех стара как мир. Французский естествоиспытатель Жорж Бюссон (1707–1788) бросал монету 4040 раз, и «орел» выпал в 2048 случаях. Английский математик Чарльз Пирсон (1857–1936) 24000 раз подбросил монету, «орел» выпал 12012 раз.
Вообще, одним из вопросов, из которого родилась теория вероятностей, был вопрос о том, как часто наступает то или иное случайное событие в длинной серии опытов, проходящих в одинаковых условиях.
Если в длинной серии одинаковых экспериментов со случайными исходами значения относительных частот появления одного и того же события близки к некоторому определенному числу, то это число принимают за вероятность данного случайного события.
О б о з н а ч е н и е: Р (А).
Подчеркиваем, что это статистическое определение вероятности. То есть специалисты-практики (статистики), интересующиеся вероятностями конкретных событий, проверяют расчеты на практике, в экспериментах. Анализируют относительную частоту наступления этого события при многократном повторении в одних и тех же условиях эксперимента или наблюдения и оценивают вероятность случайного события.
IV. Формирование умений и навыков.
Упражнения:
№ 793.
Р е ш е н и е
п = 50
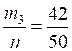 = 0,84; = 0,84; | 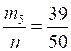 = 0,78; = 0,78;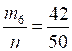 = 0,84; = 0,84; | 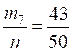 = 0,86; = 0,86;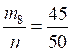 = 0,9; = 0,9;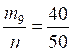 = 0,8. = 0,8. |
Можно предположить, что вероятность попадания в цель для этого стрелка 0,8.
О т в е т: Р(А) = 0,8.
№ 794.
Р е ш е н и е
п = 16; т = 9; W(A) = – относительная частота, но мы не можем утверждать, что и вероятность попадания равна , так как не было многократного повторения наблюдения.
О т в е т: нельзя.
V. Индивидуальная работа на местах.
З а д а ч и.
1. Чтобы определить, как часто встречаются в лесопарке деревья разных пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева. Результаты были занесены в таблицу:
| Породы | Сосна | Дуб | Береза | Ель | Осина | Всего |
| Число деревьев | 315 | 217 | 123 | 67 | 35 | 757 |
Оцените вероятность того, что выбранное наугад в этом парке дерево будет:
а) сосной;
б) хвойным;
в) лиственным.
Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.
Р е ш е н и е
а) P(A) = ≈ 0,416, где А – выбрана сосна;
б) P(B) =
в) P(C) =
О т в е т: а) 0,416; б) 0,505; с) 0,495.
2. По статистике, на каждые 1000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку?
Р е ш е н и е
P(A) =
О т в е т: 0,997.
3. Демографы утверждают, что вероятность рождения близнецов равна 0,012. В скольких случаях из 10000 рождений можно ожидать появления близнецов?
Р е ш е н и е
А – рождение близнецов;
Р(А) = 0,012, т – количество случаев рождения близнецов;
P(A) =