ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1036
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте основные комбинаторные правила, формулы.
– Какие определения вероятности вы знаете? Сформулируйте, приведите примеры.
Домашнее задание: № 841, № 861, № 868.
У р о к 15 (84).
КОНТРОЛЬНАЯ РАБОТА № 6
В а р и а н т 1
1. На стол бросают два игральных тетраэдра (серый и белый), на гранях каждого из которых точками обозначены числа от 1 до 4. Сколько различных пар чисел может появиться на гранях этих тетраэдров, соприкасающихся с поверхностью стола?
2. Сколько существует шестизначных чисел (без повторения цифр), у которых цифра 5 является последней?
3. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?
4. На каждой карточке написана одна из букв к, л, м, н, о, п. Четыре карточки наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании получится слово «клоп»?
5. Найдите вероятность того, что случайным образом выбранное двузначное число при делении на 11 дает в остатке 10.
В а р и а н т 2
1. Из коробки, содержащей 8 мелков различных цветов, Гена и Таня берут по одному мелку. Сколько существует различных вариантов такого выбора двух мелков?
2. Сколько существует пятизначных чисел (без повторения цифр), у которых вторая цифра в записи 4?
3. В урне 6 белых и 4 черных шара. Из этой урны наудачу извлекли 5 шаров. Какова вероятность того, что 2 из них белые, а 3 черные?
4. На каждой карточке написана одна из букв р, с, т, у, ф, х. Четыре карточки наугад выкладывают одну за другой в ряд. Какова вероятность, что при выкладывании получится слово «хруст»?
5. Найдите вероятность того, что случайным образом выбранное двузначное число при делении на 13 дает в остатке 5.
РЕШЕНИЕ ВАРИАНТОВ КОНТРОЛЬНОЙ РАБОТЫ
В а р и а н т 1
1. Первый тетраэдр может лечь на стол одной из четырех своих граней; второй тетраэдр – также одной из четырех своих граней; всего 4 ∙ 4 = 16 различных пар граней (чисел).
О т в е т: 16.
2. Фиксируем цифру 5 на последнем месте, на остальные пять перед ней выбираем любые пять цифр из 9 оставшихся (с учетом порядка выбора).
Количество вариантов
= 5 · 6 · 7 · 8 · 9 = 15120 чисел. Но мы знаем, что цифра 0 не может стоять на первом месте. Мы должны «отбросить» из этих чисел те, у которых 0 на первом месте (и 5 на последнем).Таких чисел
= 5 · 6 · 7 · 8 = 1680 чисел.Значит, всего 15120 – 1680 = 13440 вариантов.
О т в е т: 13440.
3. Исходы – все возможные четверки людей, выбираемые из членов бригады; порядок выбора не учитывается, так как все билеты равнозначные.
Общее число исходов:
= 35.Событие А – «выбраны 2 мужчины и 2 женщины», m = =
=
= 18 – количество благоприятных исходов;
.О т в е т: .
4. Исходами опыта будут расположения выбранных карточек в определенном порядке, то есть размещения
= 3 · 4 · 5 · 6 = 360 – общее число исходов.Благоприятный исход – один (слово «клоп»).
Вероятность
.О т в е т: .
5. Общее число двузначных чисел п = 90.
Событие А – «случайным образом выбранное двузначное число при делении на 11 дает в остатке 10».
Количество благоприятных исходов т равно числу значений k, при которых число 11k + 10 – двузначное. Это будет при k = 0, 1, 2, 3, 4, 5, 6, 7, 8, то есть т = 9.
Искомая вероятность
.О т в е т: 0,1.
В а р и а н т 2
1. В данном случае порядок выбора имеет значение (один цвет может попасться Гене или Тане). Гена может выбрать один из 8 мелков, а Таня – один из 7 оставшихся. Общее число вариантов выбора по правилу умножения равно 8 · 7 = 56.
О т в е т: 56.
2. Фиксируем цифру 4 на втором месте, на остальные четыре выбираем любые четыре цифры из 9оставшихся (с учетом порядка выбора). Количество вариантов
= 6 · 7 · 8 · 9 = 3024 чисел. Но мы знаем, что цифра 0 не может стоять на первом месте. Мы должны «отбросить» из этих чисел те, у которых 0 на первом месте (и 4 на втором). Таких чисел 
= 6 · 7 · 8 = 336 чисел. Значит, всего 3024 – 336 = 2688 вариантов.О т в е т: 2688.
3. Исходы – все возможные пятерки шаров, вынимаемые из урны; порядок выбора не учитывается.
Общее число исходов:
.Событие А – «выбраны 2 белых и 3 черных шара», m = =
=
= 60 – количество благоприятных исходов;
.О т в е т: .
4. Исходами опыта будут расположения выбранных карточек в определенном порядке, то есть размещения
= 2 · 3 · 4 · 5 · 6 = 720 – общее число исходов.Благоприятный исход – один (слово «хруст»).
Вероятность
.О т в е т: .
5. Общее число двузначных чисел п = 90.
Событие А – «случайным образом выбранное двузначное число при делении на 13 дает в остатке 5».
Количество благоприятных исходов т равно числу значений k, при которых число 13k + 5 – двузначное. Это будет при k = 1, 2, 3, 4, 5, 6, 7, то есть т = 7.
Искомая вероятность
.О т в е т: .
ИТОГОВОЕ ПОВТОРЕНИЕ
У р о к 1 (85).
НАХОЖДЕНИЕ ЗНАЧЕНИЯ ЧИСЛОВОГО
ВЫРАЖЕНИЯ. ПРОЦЕНТЫ
Цели: систематизировать знания учащихся; обобщить умения нахождения значения числового выражения, процента от числа и числа по его проценту.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Какие из приведенных чисел являются рациональными:
0,3; ; ; 1,(31); ; ; –4,2(51)?
2. Представьте в виде десятичной дроби число:
а) ; б) ; в) ; г) ; д) ; е) .
3. Вычислите:
.4. Найдите:
а) 3 % от 60; б) 25 % от 360.
5. Сколько процентов составляет:
а) 26 от 200; б) 50 от 250?
III. Формирование умений и навыков.
1. Начинаем с актуализации знаний, предлагая несложное задание на нахождение значения числового выражения.
Упражнения:
В а р и а н т 1
Вычислите:
а) 4 (1,22 : 0,4 – 3,7) + ;
б) + (0,4 · 3,25 – 3,15) : 0,2;
в)
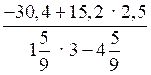.В а р и а н т 2
Вычислите:
а) + 1,2 (2,3 – 0,061 : 0,2);
б) 5,07 : (0,6 · 3,25 – 2,25) – 3 ;
в) .
Р е ш е н и е
В а р и а н т 1
а) 4 (1,22 : 0,4 – 3,7) + = 4(3,05 – 3,7) + = 4 (–0,65) + = –2,6 +
+ = –
.б) + (0,4 · 3,25 – 3,15) : 0,2 = 1,5 + (1,3 – 3,15) : 0,2 = 1,5 + (–1,85) :
: 0,2 = 1,5 – 9,25 = –7,75.
в)
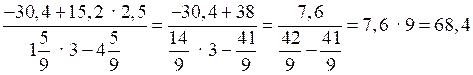.О т в е т: а) –1 ; б) –7,75; в) 68,4.
В а р и а н т 2
а) + 1,2 (2,3 – 0,061 : 0,2) = + 1,2 (2,3 – 0,305) = + 1,2 · 1,995 =
= + 2,394 =
.б) 5,07 : (0,6 · 3,25 – 2,25) – 3 = 5,07 : (1,95 – 2,25) – 3,25 = 5,07 :
: (–0,3) – 3,25 = –16,9 – 3,25 = –20,15.
в)
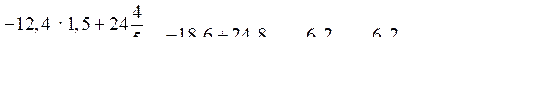
О т в е т: а)
; б) –20,15; в) –18,6.При выполнении этих заданий обращаем внимание на порядок выполнения действий, на переход от десятичных дробей к обыкновенным и наоборот.
2. Решение упражнений на нахождение значения алгебраического выражения при конкретных значениях входящих в его запись букв.
Упражнения:
В а р и а н т 1
Найдите значение выражения:
1)
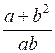, при а = , b = .2)
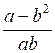, при а = 0,3 b = –0,4.3) , при х = ; у = .
В а р и а н т 2
Найдите значение выражения:
1) , при х = ; у = .
2) , при х = 1,2; у = –0,6.
3)
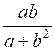, при a = ; b = .3. Решение текстовых задач на нахождение значения выражения, составленного по заданным процентным соотношениям.
№ 877 (а).
Р е ш е н и е
I с п о с о б.
Пусть а – стоимость телевизора (в рублях), тогда в апреле его стоимость составляла 1,3а. В декабре телевизор стоил (1,3а) · 0,6 = 0,78а. Так как а = 10000 (р.), то 0,78 · 10000 = 7800(р.) – стоимость телевизора в декабре.
II с п о с о б (не вводя буквенных значений).
10000 (р.) – стоимость телевизора.
1,3 · 10000 = 13000 (р.) – стоимость телевизора в апреле.
13000 · 0,6 = 78000 (р.) – стоимость телевизора в декабре.
О т в е т: 7800 р.
№ 877 (б).
Р е ш е н и е
а – цена товара первоначальная;
1,3а – цена товара после повышения на 30 %;
0,6 (1,3а) = 0,78а – цена товара после снижения на 40 %.
Значит, цена снизилась на 22 %.
О т в е т: 22 %.
П р и м е ч а н и е. Если пункт а) решать первым способом, то есть с введением буквенного выражения, то пункт б) можно решить устно.
№ 879 (б).
Р е ш е н и е
Пусть а – количество первого раствора соли, тогда 0,3а – количество соли в нем.
Пусть 2а – количество второго раствора соли, тогда 0,15 · 2а = 0,3а – количество соли в нем.
3а – количество смеси, а соли в ней 0,3а + 0,3а = 0,6а. Концентрация получившегося раствора равна
= 0,2 или 20 %.О т в е т: 20 %.
№ 881 (а).
Р е ш е н и е
8000 р. – первоначальный вклад.
1,05 · 8000 = 8400 р. – на счету через год.
1,05 · 8400 = 8820 р. – на счету через два года.
О т в е т: 8820 р.
№ 881 (б).
Р е ш е н и е
8000 р. – первоначальная сумма.
1,05 · 8000 = 8400 р. – на счету через год.
8400 + 2000 = 10400 р. – на счету на начало второго года.