ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1022
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Известно, что первый отряд прошел на 4,8 км больше, чем второй. Получим уравнение:
4х – 4у = 4,8.
На рисунке ОА = 4х и ОВ = 4у. По теореме Пифагора, получим уравнение:
(4х)2 + (4у)2 = 242.
Составим систему уравнений:
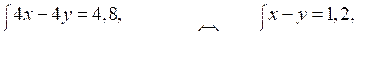
Решая систему способом подстановки, находим, что х = 4,8 и у = 3,6 (другое решение является отрицательным).
О т в е т: 4,8 и 3,6 км/ч.
Сильным в учебе учащимся можно дополнительно дать выполнить № 548.
Р е ш е н и е
Пусть х км/ч – скорость первого автомобиля, а у км/ч – скорость второго.
В первую таблицу занесем данные о прохождении каждым автомобилем всего пути, а во вторую – об их движении после встречи.
| | S | V | t | | | S | V | t |
| 1-й | 90 км | х км/ч | ч | 1-й | 1,25х км | х км/ч | 1,25 ч | |
| 2-й | 90 км | у км/ч | ч | 2-й | 0,8у км | у км/ч | 0,8 ч |
Поскольку после встречи первый автомобиль приходит в N через 1,25 ч, а второй в М через 0,8 ч, то первый на весь путь тратит на 1,25 – 0,8 = 0,45 ч больше. Получим уравнение:
= 0,45.
После встречи первый автомобиль проходит 1,25х км, а второй – 0,8у км. Получим уравнение:
1,25х + 0,8у = 90.
Составим систему:

Решая эту систему, находим, что х = 40 и у = 50.
О т в е т: 40 км/ч и 50 км/ч.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Опишите различные способы решения систем уравнений второй степени.
– Перечислите этапы решения задач на движение.
– Какие виды движения могут описываться в задаче?
– В чем заключается интерпретация полученного решения?
Домашнее задание: № 462, № 474.
Д о п о л н и т е л ь н о: № 549.
У р о к 48 Дата:
РЕШЕНИЕ ЗАДАЧ НА РАБОТУ С ПОМОЩЬЮ
СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Цель: формировать умение решать задачи на работу с помощью систем уравнений второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Объясните, почему данные системы уравнений не имеют решений.
а)
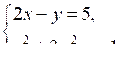 б)
б) III. Актуализация знаний.
Текстовые задачи на работу вызывают значительные затруднения у учащихся. Поэтому необходимо вспомнить основной принцип их решения и важные теоретические положения, которые пригодятся при решении таких задач.
Задачи на работу, как и задачи на движение, можно решать при помощи таблицы, выделяя предварительно все описанные процессы.
О б о з н а ч е н и я: А – работа (часто принимается за единицу);
k – производительность;
t – время.
Учащиеся должны осознать и запомнить следующее:
– k = (провести аналогию со скоростью при движении);
– если k1 – производительность первого рабочего, а k2 – производительность второго рабочего, то при их совместной работе производительность равна k1 + k2.
Затем можно выделить этапы решения задач на работу:
1) Анализ условия.
2) Выделение процессов, о которых идет речь в задаче.
3) Выбор неизвестных величин и заполнение таблицы.
4) Составление системы уравнений.
5) Решение системы уравнений.
6) Интерпретация полученных решений.
Как используется все вышеизложенное
, необходимо продемонстрировать учащимся при решении конкретной задачи, например № 467.
Р е ш е н и е
В задаче можно выделить три процесса:
– отдельная работа первого комбайнера;
– отдельная работа второго комбайнера;
– совместная работа двух комбайнеров.
Обозначим за х и у производительности первого и второго комбайнеров соответственно.
Заполним таблицу:
| | А | k | t |
| 1-й отряд | 1 | х | |
| 2-й отряд | 1 | у | |
| Вместе | 35 (х + у) | х + у | 35 |
Известно, что первый комбайнер делает всю работу на 24 ч быстрее, поэтому получим уравнение:
= 24.
Всю работу мы приняли за единицу и нашли ее выражение при совместной работе комбайнеров:
35 (х + у) = 1.
Составим систему уравнений:
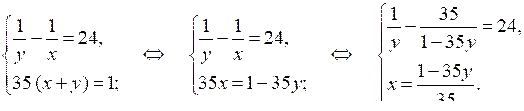
1 – 35у – 35у = 24у (1 – 35у);
1 – 70у – 24у + 24 · 35у2 = 0;
24 · 35у2 – 94у + 1 = 0;
D1 = 472 – 24 · 35 = 1369;
y1 =
y2 =
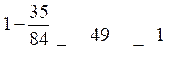 .
.Первое решение не подходит по смыслу задачи.
Из второго решения получаем, что первый комбайнер может убрать весь урожай за 60 ч, а второй – за 84 ч.
О т в е т: 60 ч и 84 ч.
IV. Формирование умений и навыков.
Упражнения:
1. № 468.
2. № 545.
3. Два строителя выложили стену из кирпичей за 14 дней, причем второй присоединился к первому через 3 дня после начала работы. Известно, что первому строителю на выполнение всей работы потребовалось бы на 6 дней больше, чем второму. За сколько дней мог бы выложить эту стену каждый строитель, работая отдельно?
Р е ш е н и е
Выделим четыре процесса:
– выполнение всей работы одним первым строителем;
– выполнение всей работы одним вторым строителем;
– трехдневная работа одного первого строителя;
– совместная работа строителей в течение 11 дней.
Заполним таблицу:
| | S | V | t |
| 1-й всю работу | 1 | х | |
| 2-й всю работу | 1 | у | |
| 1-й начало работы | 3х | х | 3 |
| Совместная работа | 11 (х + у) | х + у | 11 |
Известно, что первый строитель всю работу делает на 6 дней дольше. Получим уравнение:
= 6.
За три дня первый строитель сделал 3х всей работы, а затем они совместно сделали 11 (х + у) всей работы, закончив ее. Получим уравнение:
3х + 11 (х + у) = 1.
Составим систему:
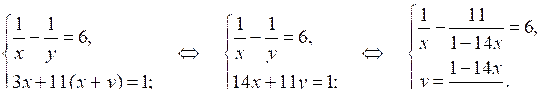
= 6;
1 – 14х – х = 6х (1 – 14х);
84х2 – 31х + 1 = 0;
D = 961 – 336 = 625;
х1 =
х2 = (не подходит по смыслу задачи).
О т в е т: 28 дней и 22 дня.
V. Итоги урока.
– Перечислите этапы решения задачи на работу.
– Что такое производительность? Как она вычисляется?
– Чему равна производительность при совместной работе?
Домашнее задание: № 466, № 546.
У р о к 49 Дата:
РЕШЕНИЕ РАЗЛИЧНЫХ ЗАДАЧ С ПОМОЩЬЮ
СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Цель: продолжить формировать умения решать задачи с помощью систем уравнений второй степени.
Ход урока
I. Организационный момент.
II. Устная работа.
Расстояние от пункта А до пункта
В равно 60 км. Один пешеход проходит его на 2 ч быстрее, чем другой. Если пешеходы выйдут одновременно навстречу друг другу, то встретятся через 5 ч.
Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода. Какая из систем уравнений соответствует условию задачи?
а) б)
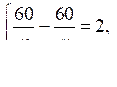 в)
в) 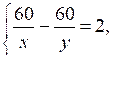
III. Проверочная работа.
В а р и а н т 1
1. Из двух пунктов, расстояние между которыми равно 18 км, вышли одновременно навстречу друг другу две группы туристов и встретились через 2 ч. Определите, с какой скоростью шла каждая группа, если известно, что на прохождение всего пути одной из них потребовалось на 54 мин больше, чем другой.
2. Один из двух подъемных кранов равной мощности может разгрузить баржу на 3 ч быстрее, чем другой. При совместной работе им потребовалось бы затратить на разгрузку баржи 6 ч 40 мин. Сколько времени требуется каждому крану, чтобы разгрузить баржу?
В а р и а н т 2
1. Из пункта А в пункт В, расстояние между которыми 360 км, выехали одновременно два автомобиля. Через 3 ч оказалось, что первый из них прошел на 30 км больше, чем второй. Найдите скорость каждого автомобиля, если известно, что на весь путь первый автомобиль затратил на полчаса меньше, чем второй.
2. Два тракториста, работая совместно, могут вспахать поле за 2 ч 40 мин. Сколько времени потребуется каждому трактористу в отдельности для выполнения этой работы, если известно, что первый из них может выполнить ее на 4 ч быстрее второго?
IV. Формирование умений и навыков.
1. № 464, № 470.
2. № 469.
Р е ш е н и е
Пусть х р. вкладчик положил в банк под у % годовых. Через год ему было начислено х · 0,01у р. Получим уравнение:
0,01ху = 400.
Через два года до начисления процентов на счету будет (х + 400) р., а после начисления процентов стало (х + 400) + (х + 400) · 0,01у р. Получим уравнение:
х + 400 + 0,01у (х + 400) = 5832.
Составим систему уравнений:
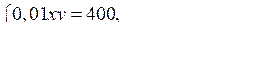
О т в е т: 5000 р., 8 %.