ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1024
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
III. Повторение учебного материала.
Неравенства вида ах2 + bx + c > 0 и ах2 + bx + c < 0, где х – переменная, а, b, c – некоторые числа и а ≠ 0, называют неравенствами второй степени с одной переменной.
А л г о р и т м р е ш е н и я:
1. Найти дискриминант трехчлена ах2 + bx + c и определить, имеет ли трехчлен корни.
2. Схематически изобразить параболу в зависимости от знака коэффициента при х2 и наличия корней.
3. Найти на оси х промежутки, для которых точки параболы расположены выше оси х или ниже оси х, в зависимости от знака решаемого уравнения.
Данный материал целесообразно представить в виде опорного конспекта или таблицы. Следует заполнить только «шапку» таблицы, содержимое заполнить либо при устном фронтальном опросе, либо организовав работу по вариантам.
| | а > 0 | a < 0 |
| 1 | 2 | 3 |
| D > 0 |  | 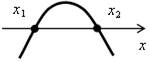 |
| ах2 + bx + c > 0 | (–∞; х1) (х1; +∞) | (х1; х2) |
| ах2 + bx + c ≥ 0 | (–∞; х1] [х1; +∞) | [х1; х2] |
| ах2 + bx + c < 0 | (х1; х2) | (–∞; х1) (х2; +∞) |
| ах2 + bx + c ≤ 0 | [х1; х2] | (–∞; х1] [х2; +∞) |
| D = 0 |  | 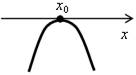 |
| ах2 + bx + c > 0 | (–∞; х0) (х0; +∞) | нет решений |
| ах2 + bx + c ≥ 0 | х – любое | {х0} |
| ах2 + bx + c < 0 | нет решений | (–∞; х0) (х0; +∞) |
| ах2 + bx + c ≤ 0 | {х0} | х – любое |
Окончание табл.
| 1 | 2 | 3 |
| D < 0 | 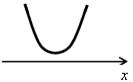 | 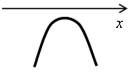 |
| ах2 + bx + c > 0 | х – любое | нет решений |
| ах2 + bx + c ≥ 0 | х – любое | нет решений |
| ах2 + bx + c < 0 | нет решений | х – любое |
| ах2 + bx + c ≤ 0 | нет решений | х – любое |
IV. Формирование умений и навыков.
При решении упражнений следует побуждать учащихся иллюстрировать полученные решения на числовой оси. Если корни квадратного трехчлена не удовлетворяют неравенству, изображаем их «выколотыми» точками.
Упражнения:
№ 1011 (а, в).
Р е ш е н и е
а) х2 + 2х – 15 < 0;
х2 + 2х – 15 = 0.
По теореме Виета, х1 · х2 = –15, х1 + х2 = –2, значит, х1 = 3; х2 = –5. Ветви параболы направлены вверх.
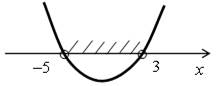
(–5; 3).
в) 10 – 3х2 ≤ 5х – 2;
– 3х2 – 5х + 12 ≤ 0;
3х2 + 5х – 12 ≥ 0;
3х2 + 5х – 12 = 0;
D = 52 – 4 · 3 · (–12) = 25 + 144 = 169 = (13)2;
х1 =
х2 =
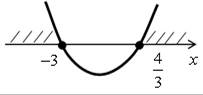
(–∞; –3] [ ; +∞).
О т в е т: а) (–5; 3); в) (–∞; –3]
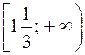 .
.№ 1012 (б, г).
Р е ш е н и е
б) (3х – 2)2 – 4х
(2х – 3) > 0;
9х2 – 12х + 4 – 8х2 + 12х > 0;
х2 + 4 > 0; х2 ≥ 0.
х2 + 4 > 4, значит, х2 + 4 > 0 для любых х.
(–∞;+∞).
г) (5х + 2) (х – 1) – (2х + 1) (2х – 1) < 27;
5х2 – 5х + 2х – 2 – 4х2 + 1 – 27 < 0;
х2 – 3х – 28 < 0;
х2 – 3х – 28 = 0.
По теореме Виета, х1 · х2 = –28, х1 + х2 = 3, значит, х1 = –4; х2 = 7. Ветви параболы направлены вверх.
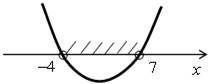
(–4; 7).
О т в е т: б) (–∞; +∞); г) (–4; 7).
№ 1013 (а).
Р е ш е н и е
Докажем, что х2 – 3х + 200 > 0 для любых х.
х2 – 3х + 200 = 0;
D = (–3)2 – 4 · 1 · 200 = –791.
D < 0, значит, корней нет. Так как ветви параболы направлены вверх, то парабола расположена выше оси х на всей числовой прямой, то есть трехчлен х2 – 3х + 200 принимает только положительные значения.
№ 1014 (а, г).
Р е ш е н и е
а)
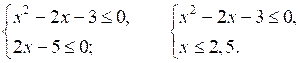
х2 – 2х – 3 = 0, по теореме Виета, х1 · х2 = –3, х1 + х2 = 2, значит, х1 = –1;
х2 = 3. Ветви параболы направлены вверх.
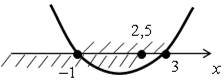
[–1; 2,5].
г)
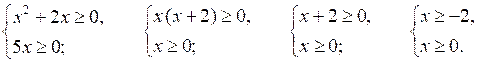
[0; +∞).
О т в е т: а) [–1; 2,5]; г) [0; +∞).
№ 1015 (а).
Р е ш е н и е
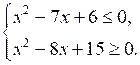
х2 – 7х + 6 = 0, по теореме Виета, х1 · х2 = 6, х1 + х2 = 7, значит, х1 = 1;
х2 = 6. Ветви параболы направлены вверх.
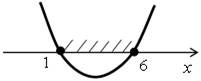
1 ≤ х ≤ 6.
х2 – 8х + 15 = 0, по теореме Виета, х1 · х2 = 15, х1 + х2 = 8, значит, х1 = 3;
х2 = 5. Ветви параболы направлены вверх.
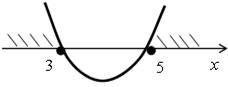
х ≤ 3 или х ≥ 5.
И м е е м:

[1; 3] [5; 6].
Объединению данных отрезков принадлежат целые решения 1; 2; 3; 5; 6.
О т в е т: 1; 2; 3; 5; 6.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какое неравенство называется неравенством второй степени с одной переменной?
– Сформулируйте алгоритм решения неравенства второй степени с одной переменной.
– Охарактеризуйте способ решения системы неравенств с одной переменной.
Домашнее задание: № 1012 (а, в), № 1014 (б, в), № 1015 (б), № 1016 (г, е).
У р о к 12 (96).
РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
Цель: актуализировать умения и навыки решения рациональных неравенств и систем рациональных неравенств методом интервалов.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Решите неравенство:
а) х2 > 9; б) х2 + 10х + 25 > 0; в) (х – 3) (х + 2) < 0.
2. При каких значениях х имеет смысл выражение:
а) ; б) ; в) ?
III. Повторение учебного материала.
На примере неравенства (х – 6) (х + 5) (х + 8) < 0 повторяем, как решаются неравенства методом интервалов.

(–∞; –8) (–5; 6).
Также необходимо вспомнить влияние кратности корня на смену знака неравенства при переходе через него.
П р и м е р. (х + 1) (х – 2) (х2 – 6х + 9) ≤ 0;
(х + 1) (х – 2) (х – 3) (х – 3) ≤ 0.

[–1; 2] {3}.
На этом примере учащиеся видят, что при нестрогом неравенстве можно случайно «потерять» отдельно стоящие корни неравенства, в нашем случае это 3.
IV. Формирование умений и навыков.
Предлагаем для решения рациональные и дробно-рациональные неравенства. Задания разбиты на группы по уровню сложности.
Упражнения:
I г р у п п а.
1. (х – 3) (х2 – 3х + 2) > 0.
Р е ш е н и е
х2 – 3х + 2 = 0, по теореме Виета,
х1 · х2 = 2, х1 + х2 = 3, значит, х1 = 2; х2 = 1.
(х – 3) (х – 2) (х – 1) > 0.

О т в е т: (0; 2) (2; 3).
2. (х2 – 1) (х – 2) (х + 3) ≤ 0.
Р е ш е н и е
(х – 1) (х + 1) (х – 2) (х + 3) ≤ 0.

О т в е т: [–3; –1] [1; 2].
3. (х2 – 3х – 4) (х2 + х – 2) < 0.
Р е ш е н и е
(х – 4) (х + 1) (х + 2) (х – 1) < 0.

О т в е т: (–2; –1) (1; 4).
II г р у п п а.
1. (х – 1)2 + х2 – 4х + 3 ≥ 0.
Р е ш е н и е
(х – 1)2 + (х – 1) (х – 3) ≥ 0;
(х – 1) (х – 1 + х – 3) ≥ 0;
(х – 1) (2х – 4) ≥ 0;
2 (х – 1) (х – 2) ≥ 0;
(х – 1) (х – 2) ≥ 0.

О т в е т: (–∞; 1] [2; +∞).
2. х2 + 5х – 24 – (х – 3) (2 – х2 + 6х) ≤ 0.
Р е ш е н и е
(х – 3) (х + 8) + (х – 3) (х2 – 6х – 2) ≤ 0;
(х – 3) (х + 8 + х2 – 6х – 2) ≤ 0;
(х – 3) (х2 – 5х + 6) ≤ 0;
(х – 3) (х – 3) (х – 2) ≤ 0;

О т в е т: (–∞; 2] {3}.
III г р у п п а.
1.
Р е ш е н и е
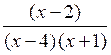 < 0.
< 0.
О т в е т: (–∞; –1) (2; 4).
2.
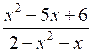 ≥ 0.
≥ 0.Р е ш е н и е
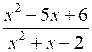 ≤ 0;
≤ 0;