Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx

Среди многообразия колебательных движений особое место занимают гармонические колебания, которые совершаются по закону sin или cos.

Простейший пример гармонического колебания - это движение математического маятника.

Ближе по своим свойствам к идеальному математическому маятнику подходит система из практически нерастяжимой очень легкой нити и к ней подвешенного груза, размеры которого малы по сравнению с длиной нити, а масса велика, по сравнению с ее массой.

На маятник в отклоненном состоянии действует возвращающая сила, направленная по касательной к траектории движения.

Уравнением движения математического маятника будет:

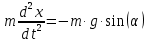(1)

При малых углах отклонения

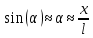
уравнение (1) принимает вид:



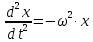
где 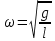- круговая или циклическая частота.

Решением этого уравнения являются функции:





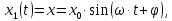
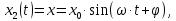
которые показывают, как изменяется смещение колеблющейся точки от положения равновесия со временем. Такие колебания характеризуют: амплитуда колебаний - величина максимального отклонения от положения равновесия. Период - интервал времени, в течение которого маятник дважды достигает смещение данной величины, т.е. время полного колебания. Частота - величина, обратная периоду, и равная числу полных колебаний.



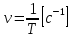
Величину 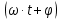называют фазой колебаний, а 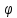- начальной фазой. Закон изменения скорости колебательного движения материальной точки можно определить, продифференцировав по времени уравнение для смещения: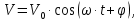



где 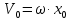. Амплитуду и начальную фазу можно определить, зная первоначальное смещение маятника от положения равновесия x_0i, и скорость V_0i: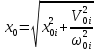

---

.

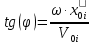За время равное периоду, фаза колебаний изменяется н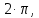а тогда 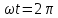откуда

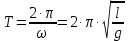(2)

Таким образом, по формуле (2) можно рассчитать период математического маятника. Другой пример гармонического движения - это движение физического маятника.

Любое тело, свободно колеблющееся вокруг неподвижной оси, не проходящей через центр тяжести, называют физическим маятником.

Момент силы тяжести, относительно оси 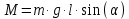направлен так, что тело двигалось к положению равновесия. По основному уравнению динамики вращательного движения: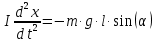



где m - масса системы; I - момент инерции тела относительно оси, l - расстояние между центром масс и осью подвеса:



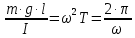
При малых углах отклонения колебания маятника будут гармоническими 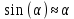и будут описываться уравнением: 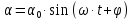, где 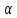- угловое смещение.

Период колебаний физического маятника определяется по формуле:



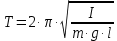
В реальных условиях на колеблющееся тело действует сила трения, приводящая к затуханию колебаний. Уравнение затухающих колебаний имеет вид:



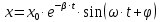
где 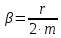- коэффициент затухания; 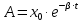- амплитуда колебаний.

Период затухающих колебаний определяется выражением:

,

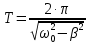где - частота собственных колебаний. Коэффициент затухания определяет скорость затухания колебаний. Его определяют как:

---

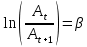т.е. логарифм отношения амплитуд затухающих колебаний, разделенных временным интервалом. Часто, быстроту затухания характеризуют логарифмическим декрементом затухания, который определяют как логарифм двух последовательных амплитуд, т.е. .

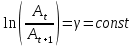Это отношение остается постоянным на всем промежутке времени затухания колебаний.

График смещений колеблющегося тела можно записать, т.е. сделать развернутым во времени. Для этого, при помощи рычагов, можно преобразовать колебательное движение точки по криволинейной траектории в колебательное движение по прямой. Этой точкой будем считать перо-фломастер, которое, касаясь листа бумаги, будет чертить траекторию колебательного движения точки в разные моменты времени.

Если перемещать лентопротягивающим устройством лист бумаги с постоянной скоростью, то получится развернутое во времени колебательное движение.

Порядок выполнения задания

ЗАДАНИЕ 1: Определение экспериментально периода колебаний маятника для случая малых смещений и при максимально возможной длине. Рассчитайте период колебаний по формуле для периодов колебаний физического и математического маятников. Сопоставьте полученные результаты и сделайте вывод относительно типа маятников.

ЗАДАНИЕ 2: Изучите зависимость периода колебаний маятника от его длины. Для этого: из 20-30 колебаний определяют период колебаний маятника при максимально возможной его длине. Изменяют его длину в 2, 3, 4 раза. Одновременно осуществляйте запись колебаний на двойном листе, прикрепленном к ленте, при заданной скорости. Измерьте все величины, характеризующие колебательное движение: амплитуду, частоту, период и запишите уравнение колебательного движения для фломастера в явном виде.

ЗАДАНИЕ 3: Определить среднее значение скорости, с которой колеблется точка фломастера при движении от крайнего положения к положению равновесия. Необходимые данные взять из графиков-данных задания 2.

Определить скорость фломастера в период прохождения его через положение равновесия. Для этого: провести касательную к точке пересечения с осью времени; графически определить значение производной. Проделать аналогичные действия и определить скорость фломастера через период.

ЗАДАНИЕ 4: Изучение затухающих колебаний.

Прикрепите флажок к одному из маятников и заставьте его колебаться (или прижмите фломастер к листу, чтобы увеличить трение). Сделайте запись графически затухающих колебаний на двойном листе. Скорость движения ленты задается такая, чтобы осуществлялось 7-10 периодов колебаний. Этому соответствует примерно второе положение на регуляторе источника питания. По графику определить логарифмический декремент затухания в области больших и средних амплитуд.

---

ЗАДАНИЕ 5: Изучение сложения колебаний, направленных в одну сторону.

Заправить двойной лист на ленте так, чтобы плоскость, проходящая через перо-фломастер, находилась справа от начала листа. Подберите амплитуду колебаний маятника примерно в 4 раза меньше чем ширина листа. Сделать запись 3-5 полных колебаний отдельно для правого и левого маятников, а потом для обоих, отклоняя на тот же угол.

ЗАДАНИЕ 6: Изучение сложения колебаний, направленных в разные стороны. Биение.

Заправить двойной лист на ленте так, чтобы плоскость, проходящая через перо-фломастер, находилась справа от начала листа. Подберите амплитуду колебаний маятников, чтобы на листе укладывался период изменения амплитуды биения.

Вопросы для допуска

1. 
   Какие движения называются колебательными? Какие колебания называются гармоническими? Негармоническими?
   
2. 
   Дайте понятия смещения, скорости, ускорения и периода гармонических колебаний.
   
3. 
   Выведите формулы сложения гармонических колебаний; одинаковых, разных частот.
   
4. 
   Выведите формулы сложения взаимно перпендикулярных гармонических колебаний.
   
5. 
   Выведите уравнение собственных, затухающих, вынужденных колебаний.
   
6. 
   Дайте понятие механического резонанса.
   
7. 
   Может ли мгновенная скорость точки быть меньше средней скорости?
   
8. 
   Методика выполнения лабораторной работы.
   

Вопросы для защиты

Решение задачи на тему гармонические колебания.

Лабораторная работа № 15

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ И ОПРЕДЕЛЕНИЕ

ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ

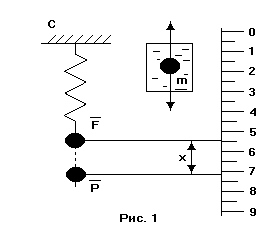
Приборы и принадлежности: пружинный маятник с грузом, шкала (линейка), сосудом с жидкостью, секундомер.

Цель работы: изучение затухающих колебаний с помощью пружинного маятника.

ВВЕДЕНИЕ

Если пружинный маятник (рис. 1) привести в движение в несопротивляющей среде (свободные колебания), то он будет совершать гармонические колебания по закону:

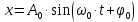(1)

В этой формуле:

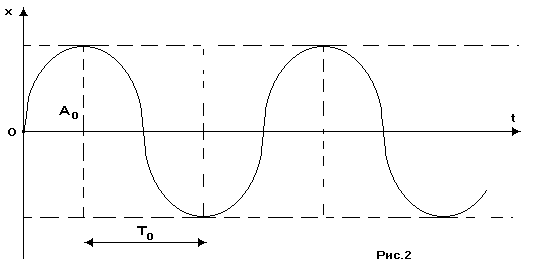
А₀ - амплитуда колебаний (см. рис. 2);

- угловая частота этих колебаний;

₀ - начальная фаза этих колебаний.

Реакция пружины:

---

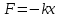
(2)

где k - жесткость пружины.





Еслиm - масса колеблющегося тела, то собственная угловая частота:

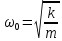(3)

Частота гармонического колебания

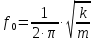(4)

в период

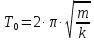(5)

Гармонические колебания совершаются с помощью постоянной амплитуды и частоты.

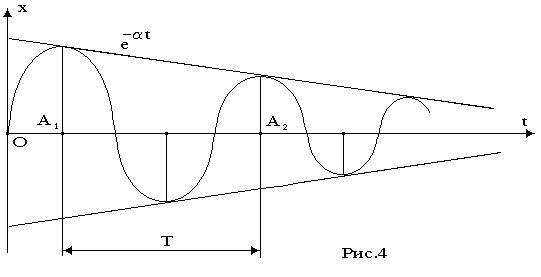
В сопротивляющей среде (например, в жидкости) колеблющееся тело, благодаря наличию трения будет совершать уже затухающие колебания (рис.3 и 4). Уравнение этих колебаний:

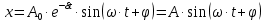(6)

Как видим, амплитуда колебаний уменьшается по экспоненциальному закону (рис. 4).

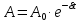(7)

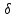- коэффициент затухания.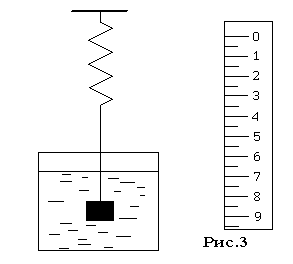



Если рассмотреть отношение амплитуды затухающих колебаний через период

,

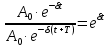то можно сделать заключение, что оно является величиной постоянной и свидетельствует о том, что амплитуда затухающих собственных колебаний за каждый период убывает в одно и то же число раз. Натуральный логарифм этого отношения называется логарифмическим декрементом затухания:

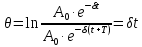(8)

При наличии трения, со временем убывает не только амплитуда, но и частота:

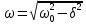(9)

соответственно период колебаний

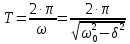, (10)

- угловая частота незатухающих колебаний (см. формулу 3).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Определить собственную частоту свободных гармонических колебаний грузика пружинного маятника. Для этого заметьте положение стрелки ненагруженного маятника (рис. 1), а затем положение стрелки с подвешенным грузиком (при отсутствии колебаний). Узнав, таким образом, статистическое

---