Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx

Задание № 3. Проверка теоремы Штейнера.

При помощи трифелярного подвеса может быть также проверена теорема Штейнера.

Зная момент инерции I₀ какого-либо тела относительно оси вращения, проходящей через его центр масс, момент инерции I относительно любой оси ей параллельной и, отстоящей от нее на расстоянии r, может быть определен следующим образом:

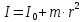. (5)

Воспользовавшись (для нашей работы) одним из свойств момента инерции (аддитивность), момент инерции одного груза m относительно оси вращения, проходящей через его центр масс, можем вычислить так:

Один груз в центре 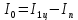(6)

Два груа в центре 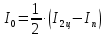. (7)

Тогда момент инерции одного груза m относительно оси вращения, проходящей через середины первых (от центрального отверстия на платформе) отверстий, будет равен:

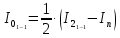. (8)

Тогда момент инерции одного груза m относительно оси вращения, проходящей через середины вторых (от центрального отверстия на платформе) отверстий, будет равен:

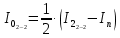. (9)

Аналогично для оси вращения, проходящей через середины третьих (от центрального отверстия на платформе) отверстий, имеем:

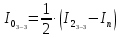. (10)

З ная (Рис. 4) расстояние r₁ между центральным и первым от центра отверстиями, расстояние r₂ между центральным и вторым от центра отверстиями, расстояние r₃ между центральным и третьим от центра отверстиями, не забывая, что момент инерции цилиндрического тела массой m относительно оси, проходящей через центр масс параллельно образующей, рассчитывается по формуле: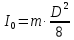

, (11)

где D – диаметр груза, определим моменты инерции одного тела массы m относительно осей, проходящих через середины первого, второго и третьего отверстий, следующим образом (по теореме Штейнера; формула (5)):

---

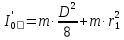
, (12)

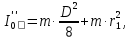(13)

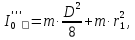(14)

Проверка теоремы Штейнера будет заключаться в следующем: моменты инерции одного груза массы m, полученные аналитическим способом (12, 13 и 14), а также согласно практическим измерениям (8, 9 и 10) должны быть тождественно (примерно) равны. То есть:



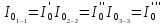
(Моменты инерции одного тела массы m относительно оси вращения, проходящей через его центр масс, рассчитанные по формулам (6), (7) и (11) также должны быть тождественно (примерно) равны.)

Примечание. Измерение расстояний (между центрами отверстий) r₁ , r₂ и r₃, а также диаметра груза D провести при помощи линейки (с точностью до 1 мм) и штангенциркуля (с точностью до 0,05 мм) по три раза и взять средние арифметические значения. Масса m указана на самом грузе. Результаты измерений и вычислений (для удобства) занести в таблицу. Сделать подробный вывод по всей проделанной работе.

m, кг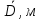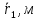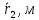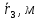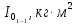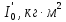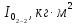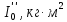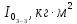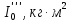

---

Вопросы для допуска

1. 
   Поступательное и вращательное движения. Сложение движений твердого тела. Степени свободы.
   
2. 
   Понятие момента силы. Момент силы относительно оси вращения. Пара сил.
   
3. 
   Понятие момента инерции материальной точки и момента инерции твердого тела.
   
4. 
   Основное уравнение динамики вращательного движения твердого тела около неподвижной оси (вывод уравнения). Понятие момента импульса.
   
5. 
   Свойства момента инерции.
   
6. 
   Теорема Штейнера о параллельных осях (с доказательством).
   
7. 
   Вычисление момента инерции кольца (обруча), диска (сплошного цилиндра), стержня, шара – относительно оси, проходящей через центр масс.
   
8. 
   Теорема о моменте инерции плоских тел (с доказательством).
   
9. 
   Полная кинетическая энергия движущегося тела.
   
10. 
    Закон сохранения момента импульса.
    
11. 
    Вывод расчетной формулы. Методика выполнения работы.
    

Вопросы для защиты

Решение задачи на тему динамики вращательного движения.
Лабораторная работа № 12

Определение скорости звука в твердых телах

методом Кундта и расчет модуля Юнга

Цель работы: изучение стоячих волн; определение скорости звука в твердых телах, расчет модуля Юнга.

Принадлежности: лабораторная установка Кундта, миллиметровая линейка, термометр, фланель, пропитанная канифолью.

Введение

Известно, что при прохождении акустической волны из одной среды в другую, частота колебаний сохраняется, но изменяется скорость распространения волны, что приводит, в свою очередь, к изменению длины волны. Для двух различных сред можно записать:



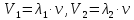
где 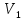и 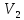– скорости распространения акустической волны в первой и во второй средах, соответственно; 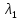и 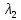– длины акустической волны в первой и во второй средах, соответственно;

---

– частота колебаний.

Поделив эти уравнения одно на другое, получим:

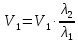. (1)

Если одна из сред, например, вторая, – газ, то скорость звука определяется по формуле Лапласа:

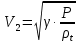, (2)

где P – давление газа, – плотность газа в зависимости от температуры, g – коэффициент Пуассона (отношение удельные теплоемкостей).

Зависимость плотности газа от изменения температуры выглядит следующим образом:

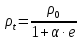, (3)

где – плотность газа при температуре 0⁰С, 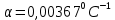– коэффициент объемного расширения газа, t – температура газа.

Подставив выражение (3) в выражение (2) (и подразумевая, что газ – это воздух) получаем:

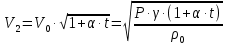(4)

где 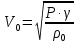– скорость распространения звуковых волн в воздухе при температуре 0⁰C и нормальном атмосферном давлении (760 мм. рт. ст.).

Подставив полученную формулу (4) в выражение (1) имеем:

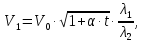(5)

Описание установки и методики измерения.

Установка Кундта (Рис. 1) состоит из стеклянной трубки 1, запаянной с одного конца, и стержня 2, из материала (латунь), в котором хотят измерить скорость распространения звука. На конце стержня имеется легкий диск 3. Зажимом 4 стержень закрепляется строго (почему?) на своей середине. В трубку насыпают немного пробковых опилок и, положив ее на подставку 5, располагают стержень внутри трубки таким образом, чтобы диск 3 не касался ее стенок.



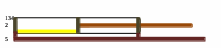
Свободный конец стержня натирают (в направлении от середины) фланелью, пропитанной канифолью, возбуждая тем самым собственные продольные колебания частиц стержня. При принятом здесь способе возбуждения, возникают в основном собственные колебания с минимальной частотой. Они представляют собой

---

стоячие волны. В месте зажима стержня частицы находятся в покое (амплитуда колебаний равна нулю). Здесь узел смещения и узел скоростей. Во всех остальных точках стержня амплитуды колебаний не равны нулю и возрастают к концам стержня, где имеются пучности смещений и узлы скоростей. На стержне длиныL укладывается половина (почему?) длины волны , поэтому можем записать: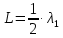

. (6)

В полости трубки (в воздушном столбе) также устанавливаются колебания, которые распределяют пробковые опилки в характерные фигуры Кундта. Когда расстояние от диска 3 до закрытого конца трубки будет равно целому числу длин полуволн, фигуры Кундта образуются особенно легко и ясно, что объясняется совпадением частоты колебания стержня с одной из собственных частот колебания столба воздуха в трубке. В результате такого совпадения увеличивается амплитуда колебаний столба воздуха в трубке (акустический резонанс).

Чтобы получить отчетливые фигуры Кундта необходимо при возбуждении колебаний (при натирании стержня) стеклянную трубку смещать в одну или другую сторону, изменяя тем самым частоты собственных колебаний столба воздуха, и добиваясь совпадения одной из этих частот с частотой колебания стержня (при этом будет слышен характерный звук). Получив отчетливые фигуры, измеряют длину нескольких фигур и определяют среднюю длину одной фигуры. Ясно, что длина одной фигуры l равна половине длины волны , распространяющейся в воздухе, то есть: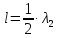

(7)

Подставив зависимости (6) и (7) в выражение (5) получим формулу для вычисления скорости распространения звука в твердых телах:

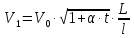. (8)

Таким образом, если измерить длину стержня L и длину фигуры Кундта l, можно по формуле (8) вычислить скорость распространения звуковой волны в латунном стержне, температуры t посмотреть по термометру.

Определив скорость

---