Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 162
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
служат числа 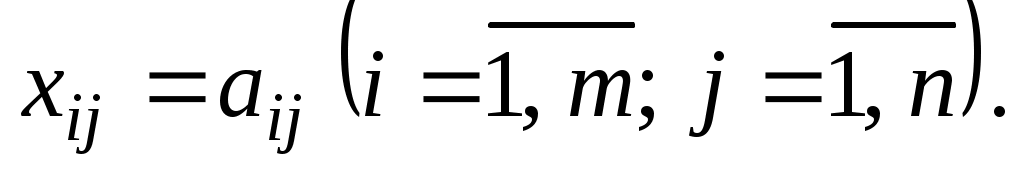 Таким образом, можно найти
Таким образом, можно найти
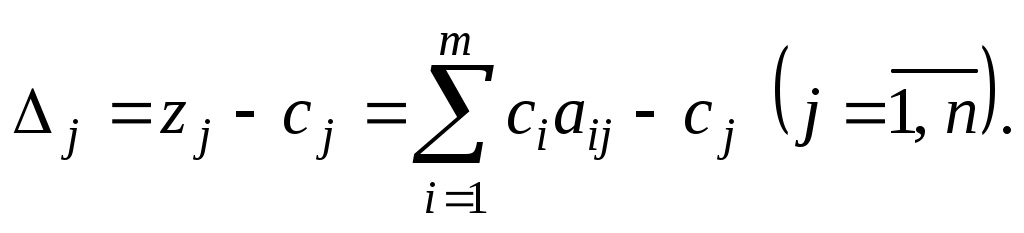
Определение 1.13. Решение системы линейных уравнений (55), определяемое базисом
системы линейных уравнений (55), определяемое базисом  , называется псевдопланом задачи (54) - (56), если
, называется псевдопланом задачи (54) - (56), если  для любого
для любого 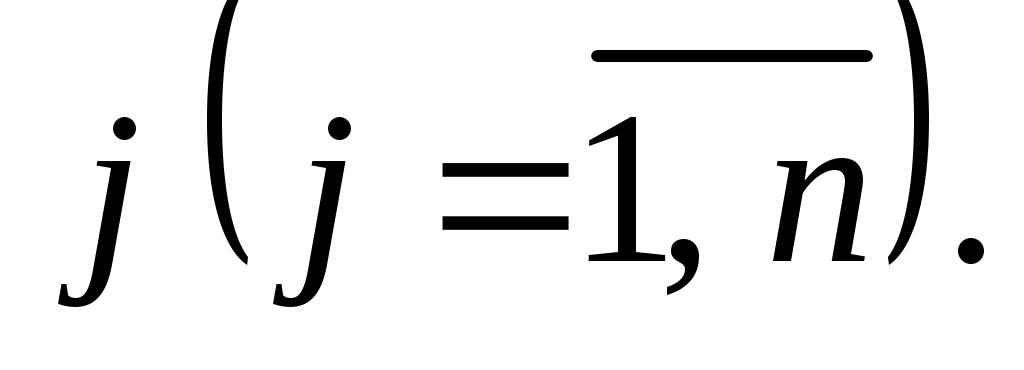
Теорема__1.13.'>Теорема 1.13. Если в псевдоплане , определяемом базисом
, определяемом базисом  , есть хотя бы одно отрицательное число
, есть хотя бы одно отрицательное число 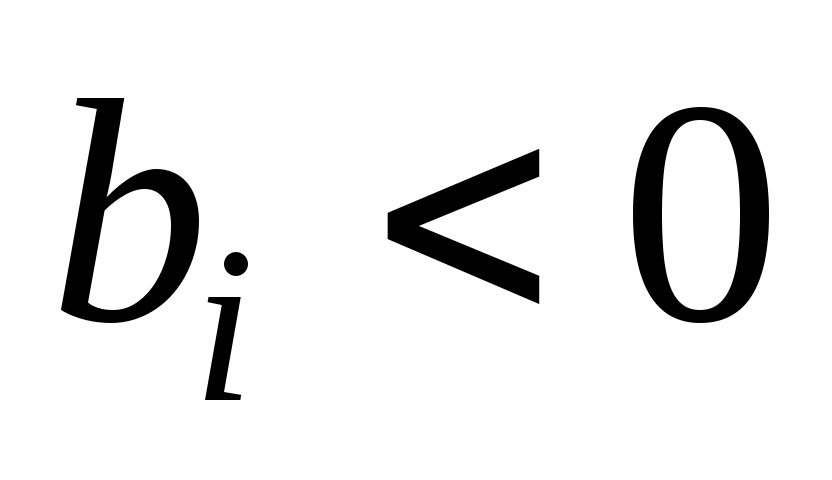 такое, что все
такое, что все 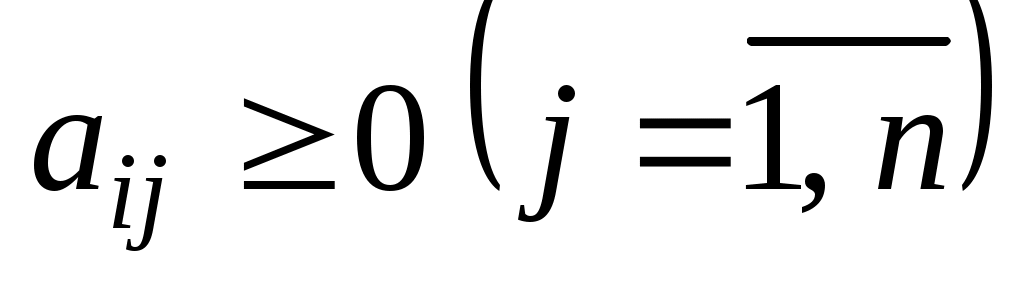 , то задача (54) - (56) вообще не имеет планов.
, то задача (54) - (56) вообще не имеет планов.
Теорема 1.14. Если в псевдоплане , определяемом базисом
, определяемом базисом  , имеются отрицательные числа
, имеются отрицательные числа 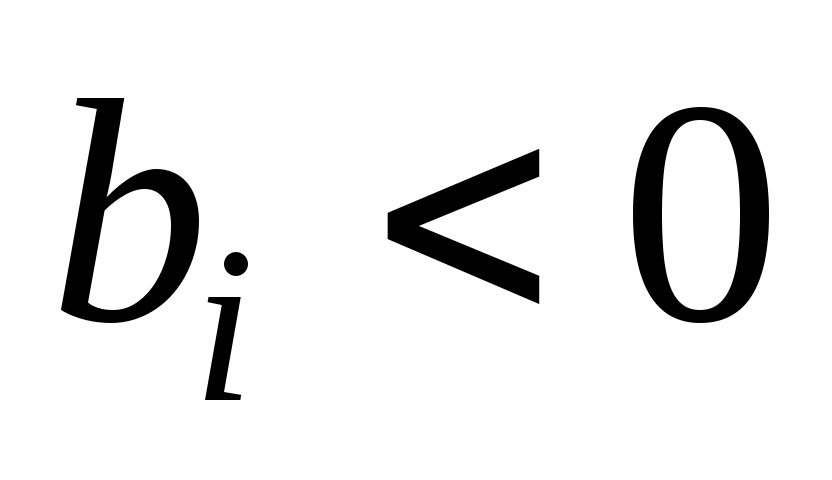 такие, что для любого из них существуют числа
такие, что для любого из них существуют числа 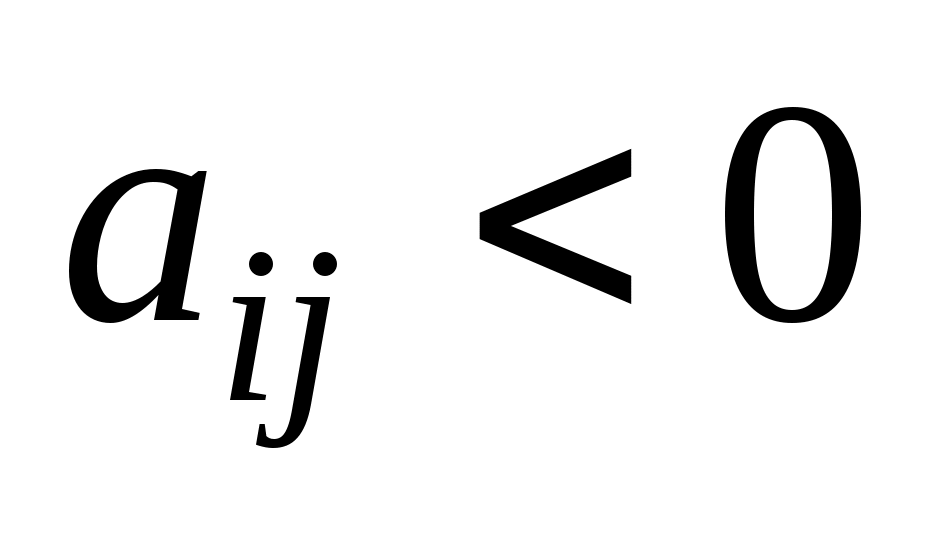 , то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (54) - (56) не уменьшится.
, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (54) - (56) не уменьшится.
Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.
Итак, продолжим рассмотрение задачи (54) - (56). Пусть — псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу (табл. 15), в которой некоторые элементы столбца вектора
— псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу (табл. 15), в которой некоторые элементы столбца вектора  являются отрицательными числами. Если таких чисел нет, то в симплекс-таблице записан оптимальный план задачи (54) - (56), поскольку, по предположению, все
являются отрицательными числами. Если таких чисел нет, то в симплекс-таблице записан оптимальный план задачи (54) - (56), поскольку, по предположению, все
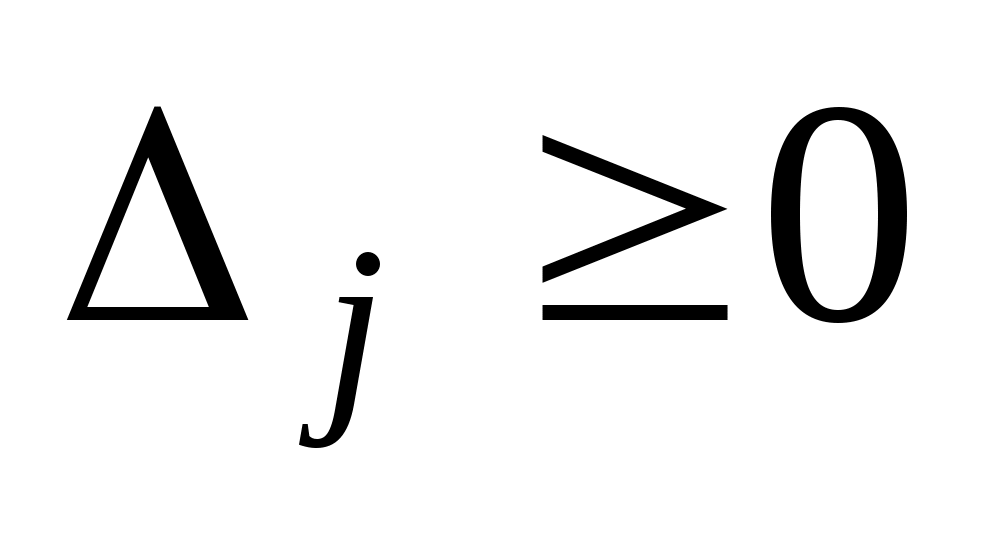 . Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс-таблицы к другой до тех пор, пока из столбца вектора
. Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс-таблицы к другой до тех пор, пока из столбца вектора  не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы (т +1)-й строки, т.е.
не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы (т +1)-й строки, т.е. 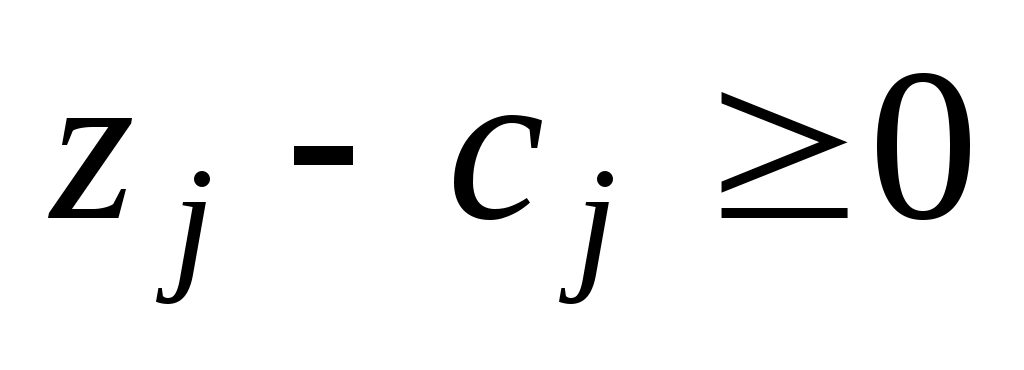 для любого
для любого 
Таким образом, после составления симплекс-таблицы проверяют, имеются ли в столбце вектора отрицательные числа. Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое-нибудь одно из них: пусть это число bl. Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится вектор Pl. Чтобы определить, какой вектор следует ввести в базис, находим
отрицательные числа. Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое-нибудь одно из них: пусть это число bl. Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится вектор Pl. Чтобы определить, какой вектор следует ввести в базис, находим 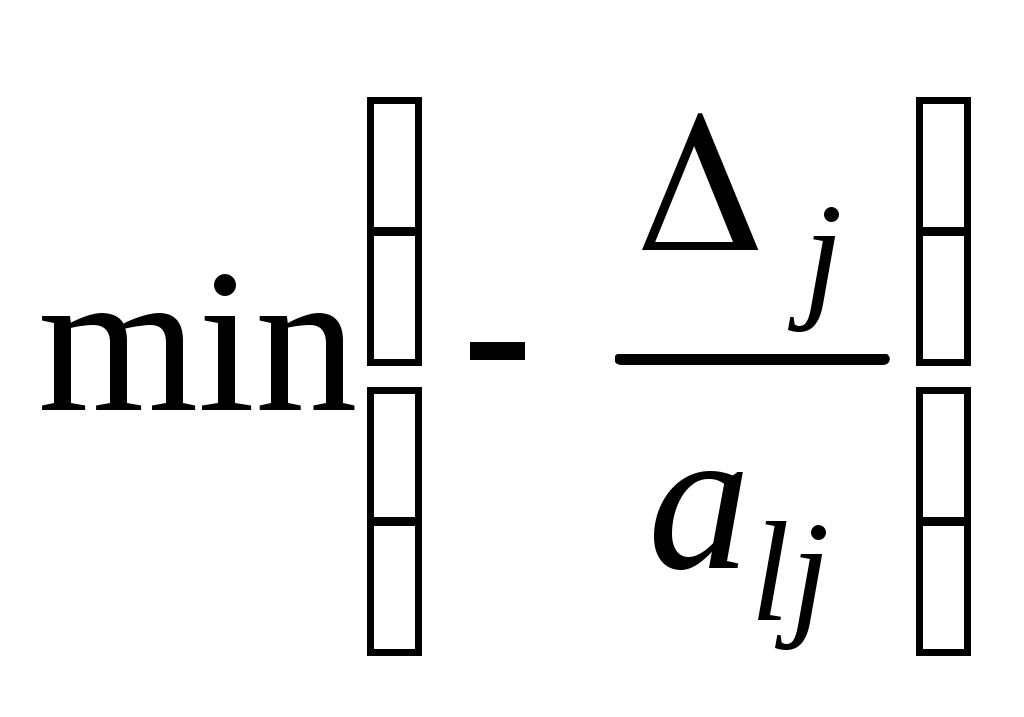 , где
, где 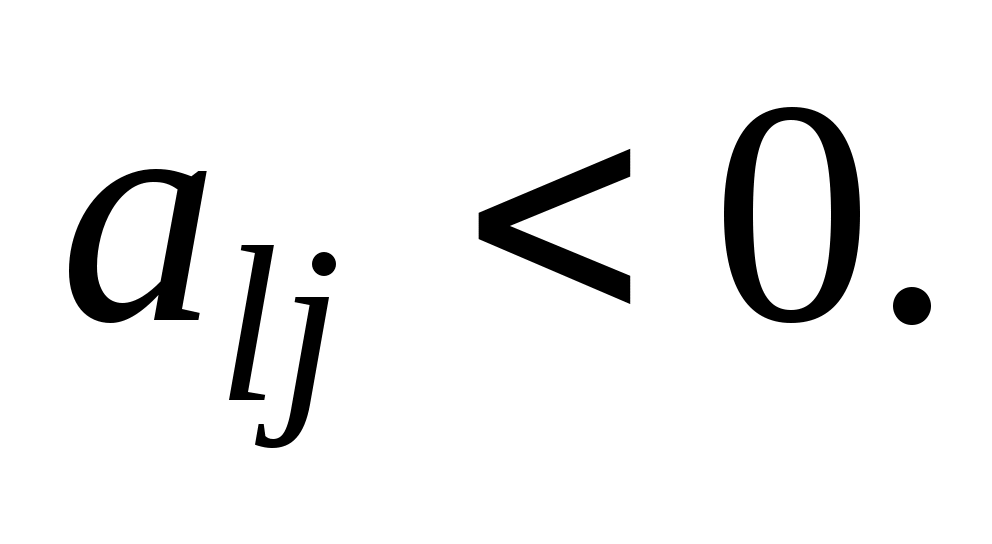
Пусть это минимальное значение принимается при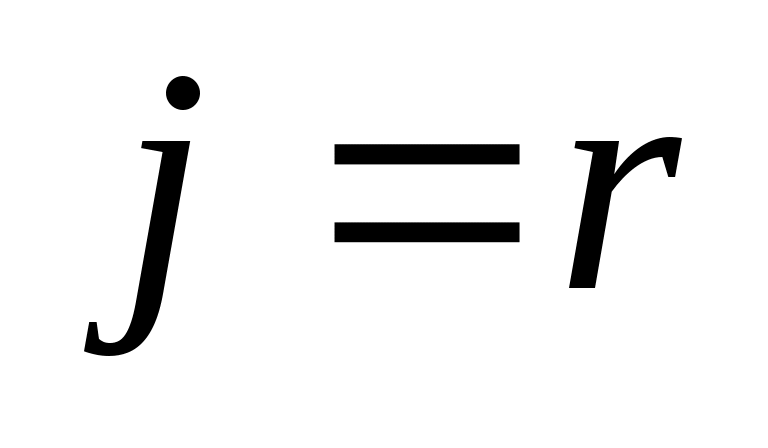 , тогда в базис вводят вектор Рr. Число
, тогда в базис вводят вектор Рr. Число 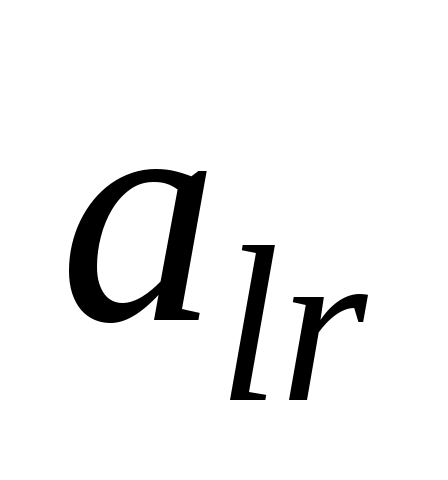 является разрешающим элементов. Переход к новой симплекс-таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектора Р0 не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что в i-й строке симплекс-таблицы (табл. 15) в столбце вектора Р0 стоит отрицательное число bi,а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.
является разрешающим элементов. Переход к новой симплекс-таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектора Р0 не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что в i-й строке симплекс-таблицы (табл. 15) в столбце вектора Р0 стоит отрицательное число bi,а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.
Таким образом, отыскание решения задачи (54) - (56) двойственным симплекс-методом включает следующие этапы:
1. Находят псевдоплан задачи.
2. Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.
3. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора Р0 и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов (m+1)-и строки к соответствующим отрицательным элементам разрешающей строки.
4. Находят новый псевдоплан и повторяют все действия, начиная с этапа 2.
Таблица 15
1.16. Найти максимальное значение функции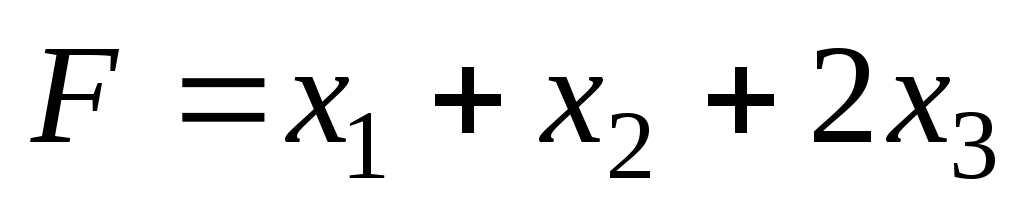 при условиях
при условиях
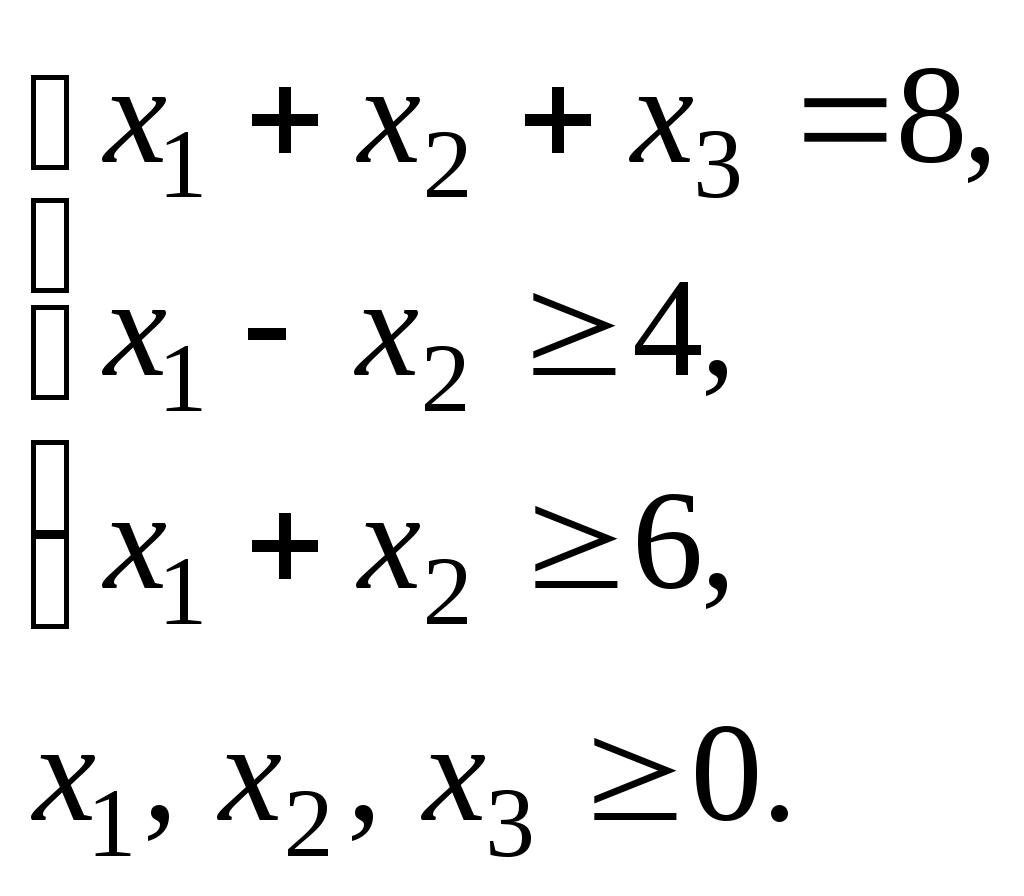
Решение. Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции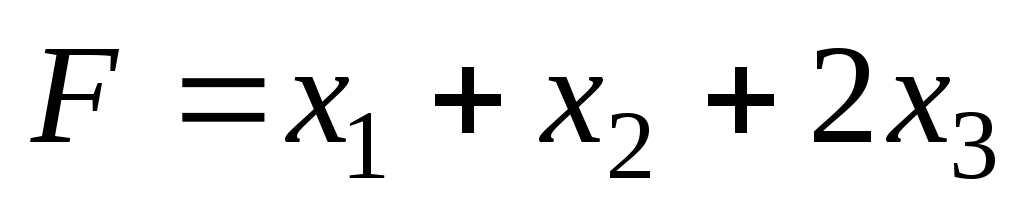 при условиях
при условиях
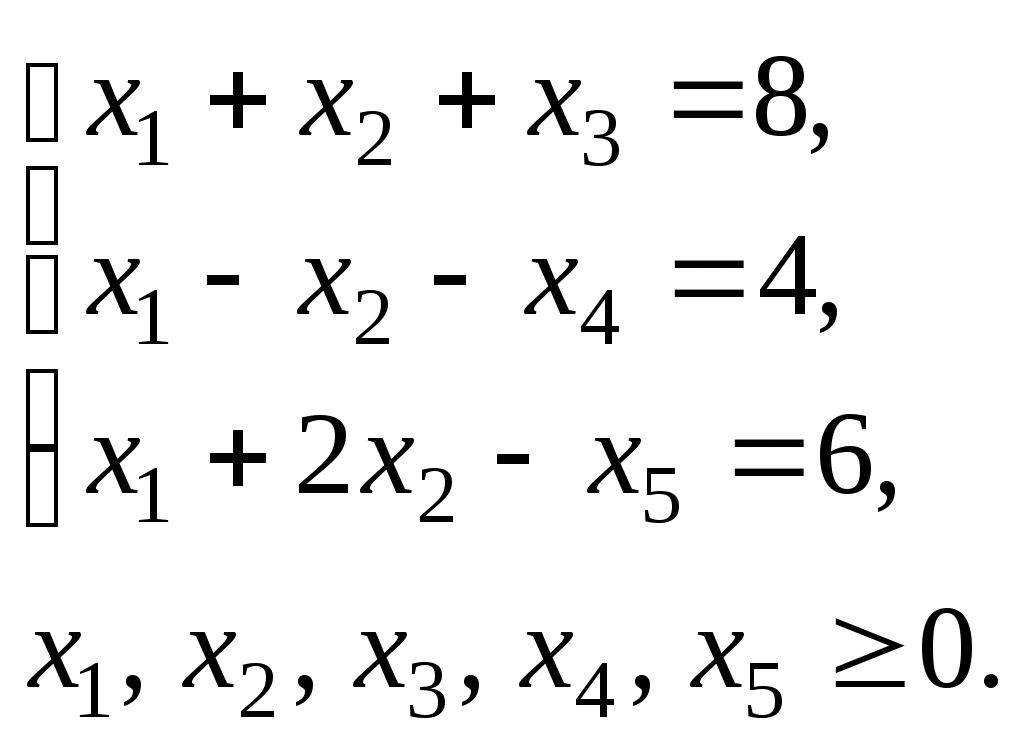
Умножим второе и третье уравнения системы ограничении последней задачи на -1 и переходим к следующей задаче: найти максимум функции
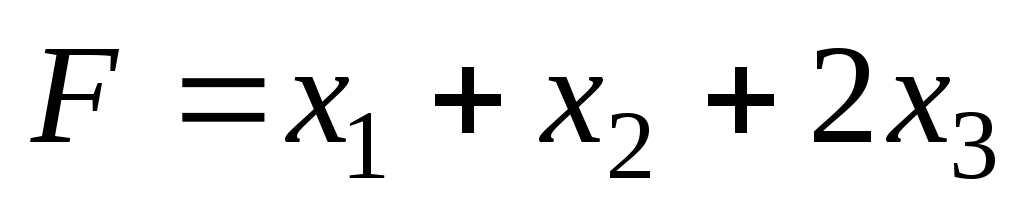 (57)
(57)
при условиях
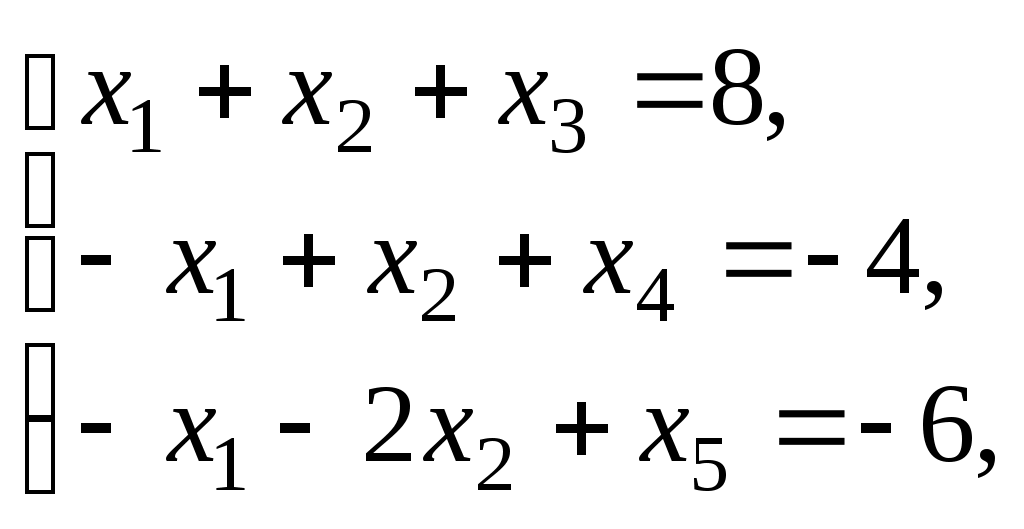 (58)
(58)
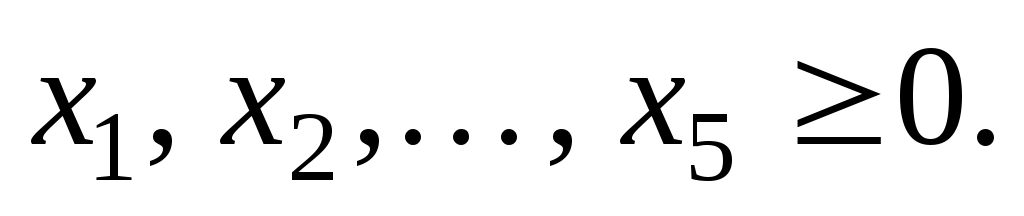 (59)
(59)
Составим для последней задачи двойственную. Такой является задача, в результате решения которой требуется найти минимальное значение функции
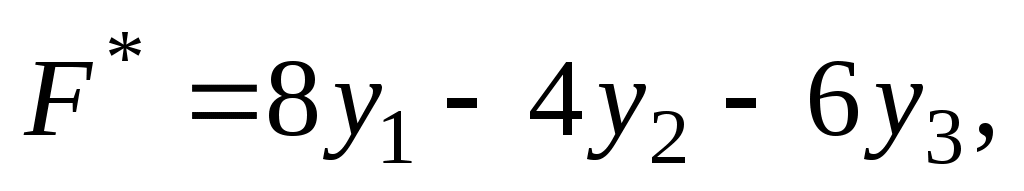 (60)
(60)
при условиях
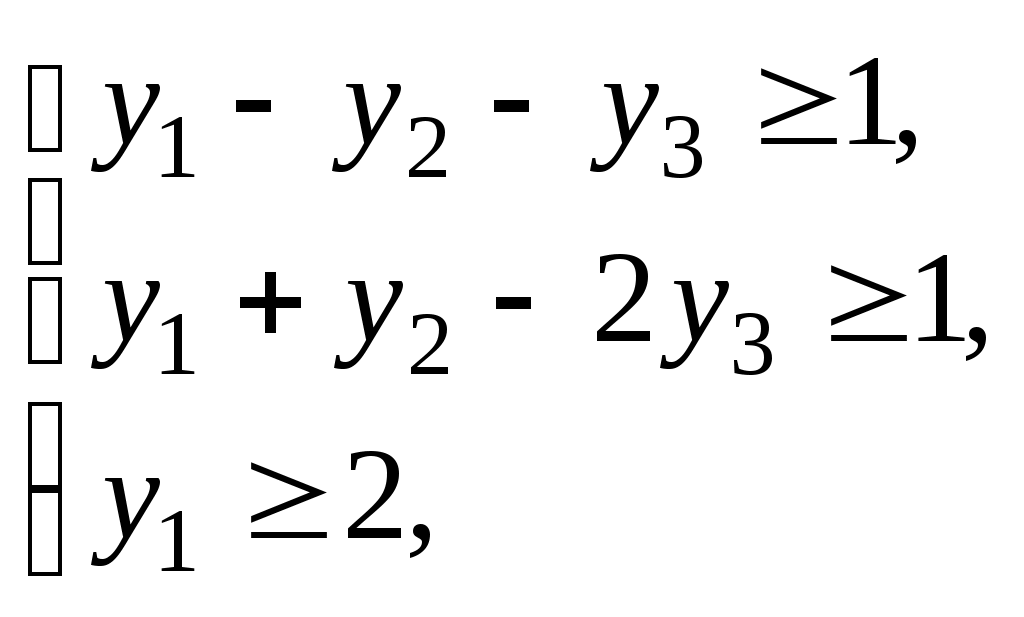 (61)
(61)
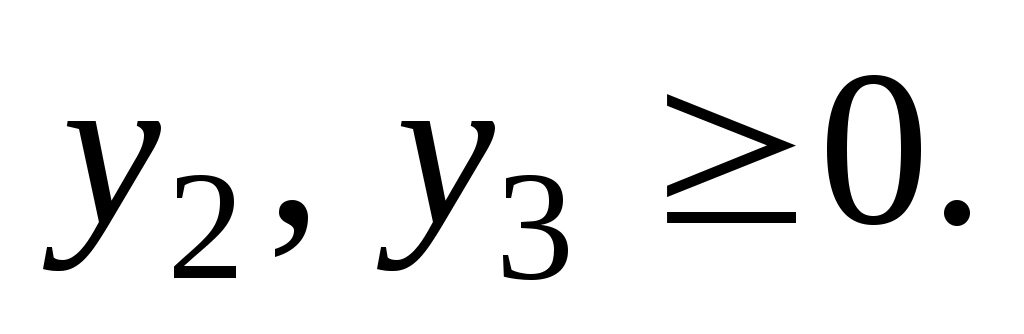 (62)
(62)
Выбрав в качестве базиса векторы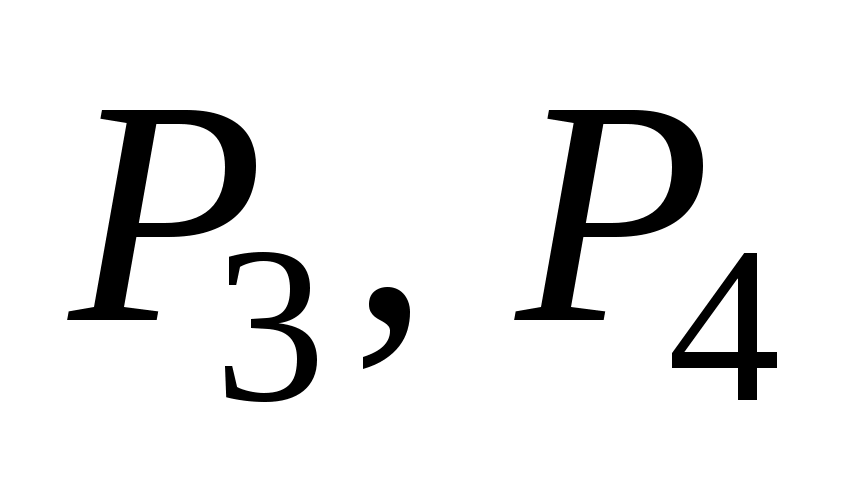 и
и 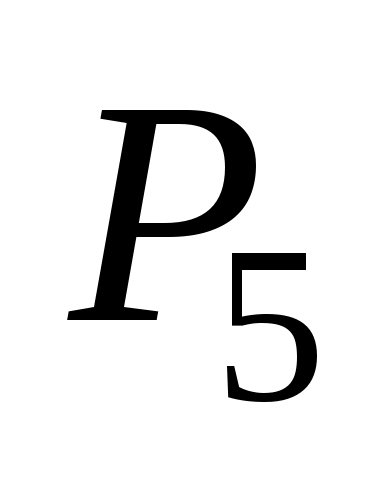 , составим симплексную таблицу (табл. 16) для исходной задачи (57) - (59).
, составим симплексную таблицу (табл. 16) для исходной задачи (57) - (59).
Таблица 16
Из этой таблицы видим, что планом двойственной задачи (57) - (59) является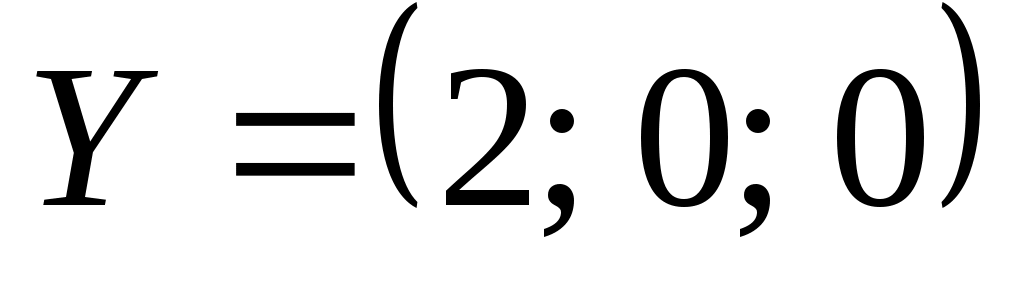 . При этом плане
. При этом плане 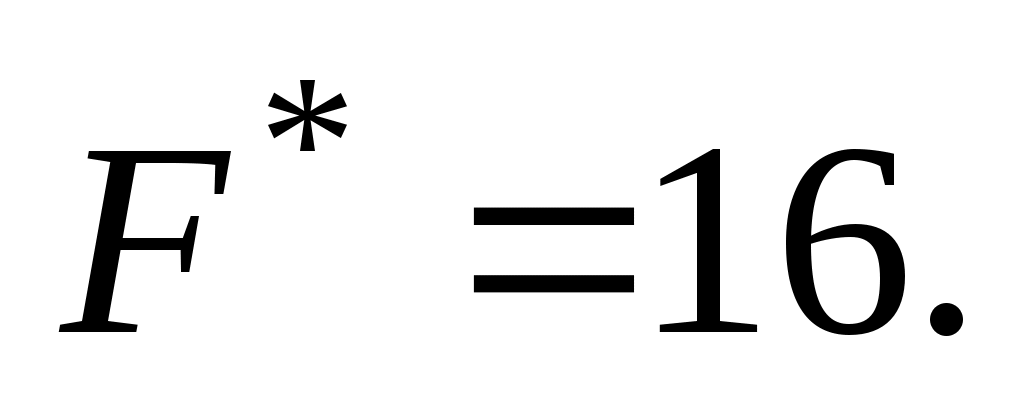 Так как в столбце вектора Р0 таблица 16 имеются два отрицательных числа (-4 и -6), а в 4-й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. (В данном случае это можно сделать, так как в строках векторов Р4и Р5 имеются отрицательные числа. Если бы они отсутствовали, то задача была бы неразрешима.) Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора Р0. В данном случае это число -6. Следовательно, из базиса исключаем вектор Р5. Чтобы определить, какой вектор необходимо ввести в базис, находим
Так как в столбце вектора Р0 таблица 16 имеются два отрицательных числа (-4 и -6), а в 4-й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс-метода переходим к новой симплекс-таблице. (В данном случае это можно сделать, так как в строках векторов Р4и Р5 имеются отрицательные числа. Если бы они отсутствовали, то задача была бы неразрешима.) Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора Р0. В данном случае это число -6. Следовательно, из базиса исключаем вектор Р5. Чтобы определить, какой вектор необходимо ввести в базис, находим 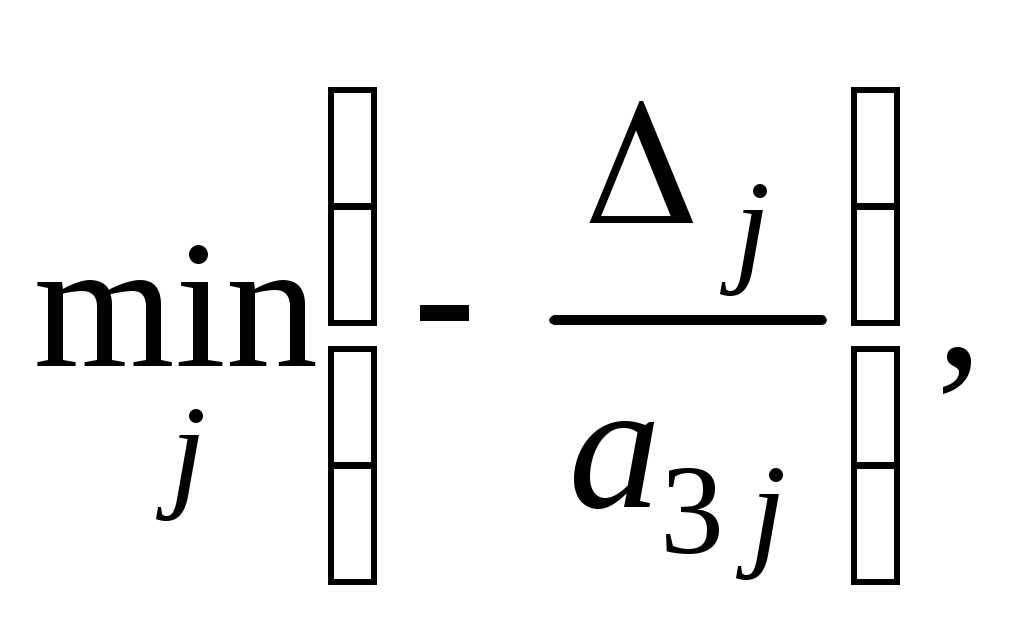 где
где 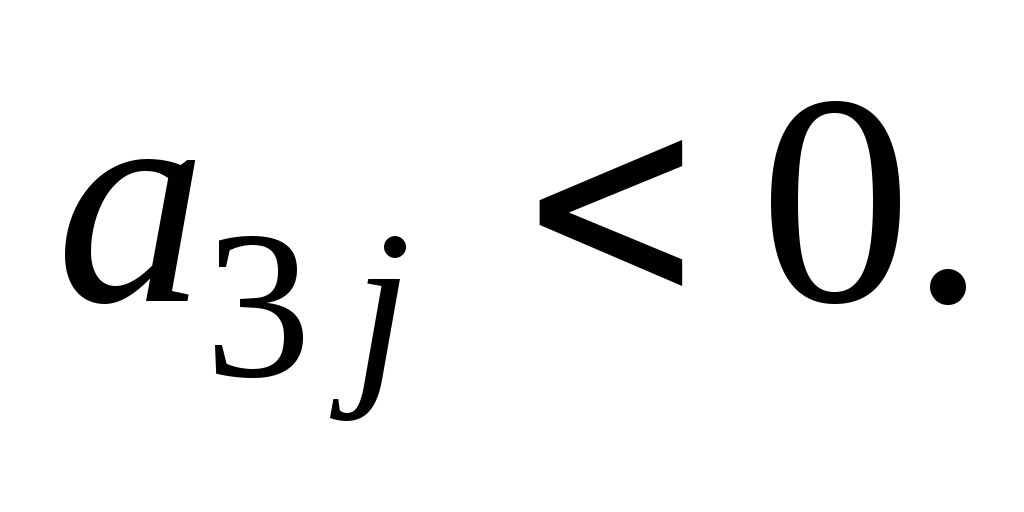 Имеем
Имеем
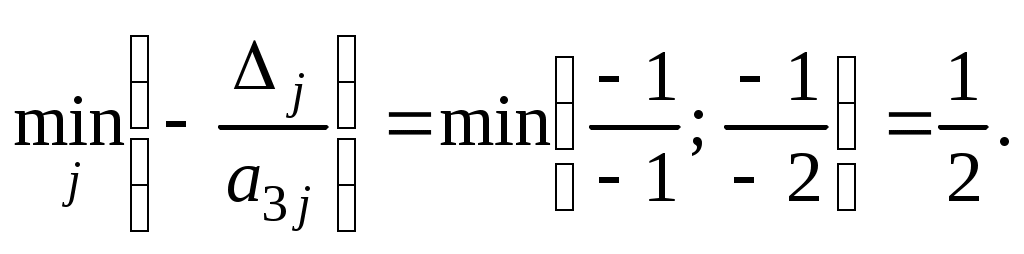
Значит, в базис вводим вектор P2. Переходим к новой симплекс-таблице (табл. 17).
Таблица 17
Из этой таблицы видно, что получен новый план двойственной задачи
Определение 1.13. Решение
Теорема__1.13.'>Теорема 1.13. Если в псевдоплане
Теорема 1.14. Если в псевдоплане
Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.
Итак, продолжим рассмотрение задачи (54) - (56). Пусть
Таким образом, после составления симплекс-таблицы проверяют, имеются ли в столбце вектора
Пусть это минимальное значение принимается при
Таким образом, отыскание решения задачи (54) - (56) двойственным симплекс-методом включает следующие этапы:
1. Находят псевдоплан задачи.
2. Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.
3. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора Р0 и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов (m+1)-и строки к соответствующим отрицательным элементам разрешающей строки.
4. Находят новый псевдоплан и повторяют все действия, начиная с этапа 2.
Таблица 15
| i | Базис | Cб | P0 | c1 | c2 | … | ce | … | cm | cm+1 | … | cr | … | cn |
| | P1 | Р2 | … | Рe | | Рm | Рm+1 | | Рr | | Рn | |||
| | | | | | | | | | | | | | | |
1.16. Найти максимальное значение функции
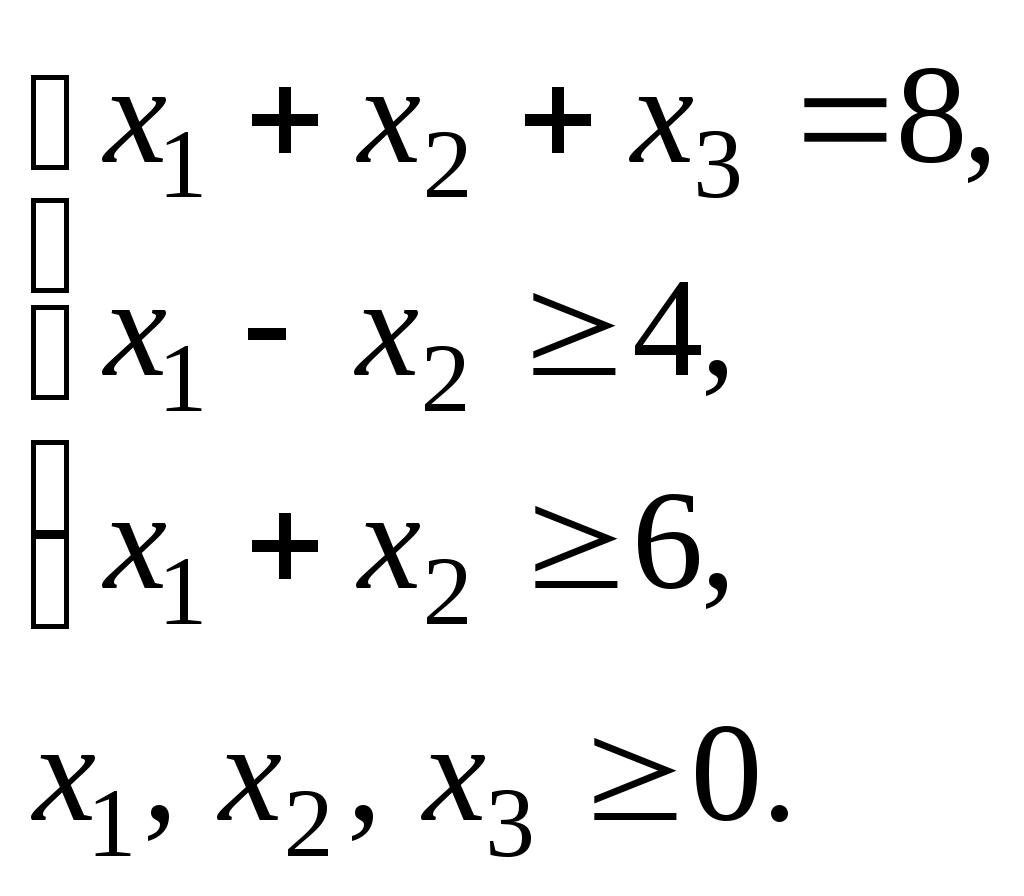
Решение. Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции
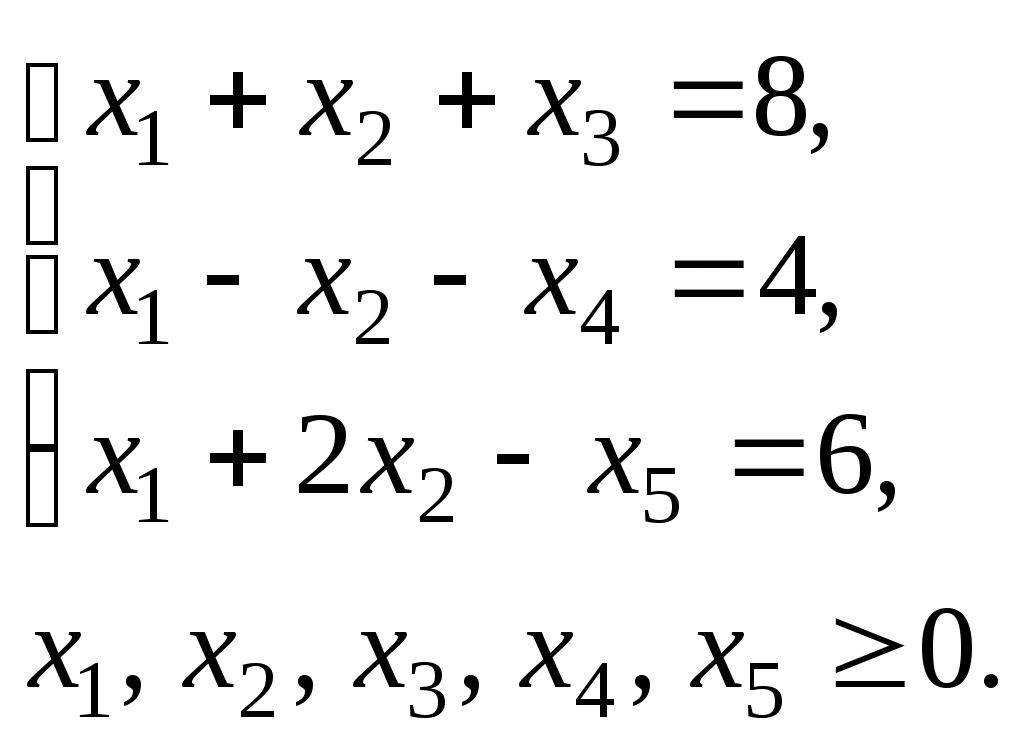
Умножим второе и третье уравнения системы ограничении последней задачи на -1 и переходим к следующей задаче: найти максимум функции
при условиях
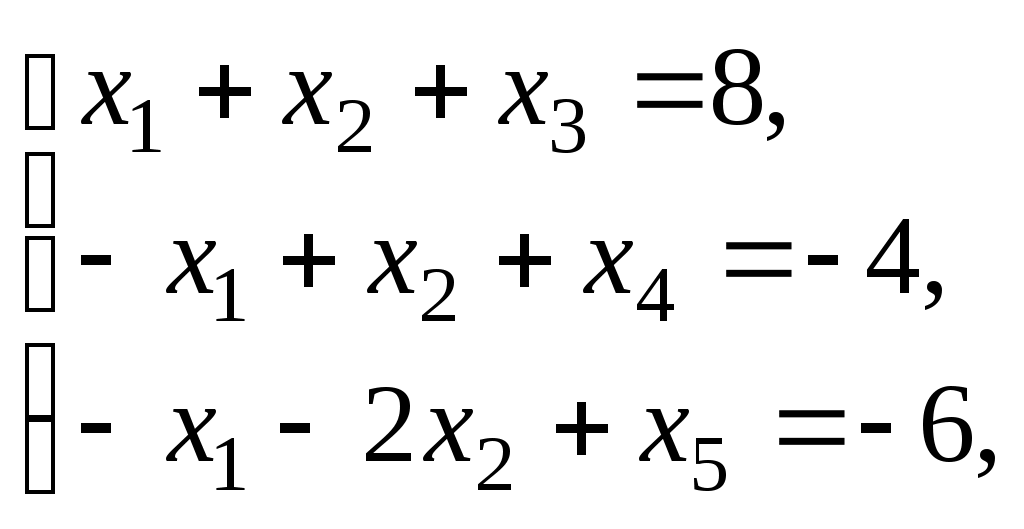 (58)
(58)Составим для последней задачи двойственную. Такой является задача, в результате решения которой требуется найти минимальное значение функции
при условиях
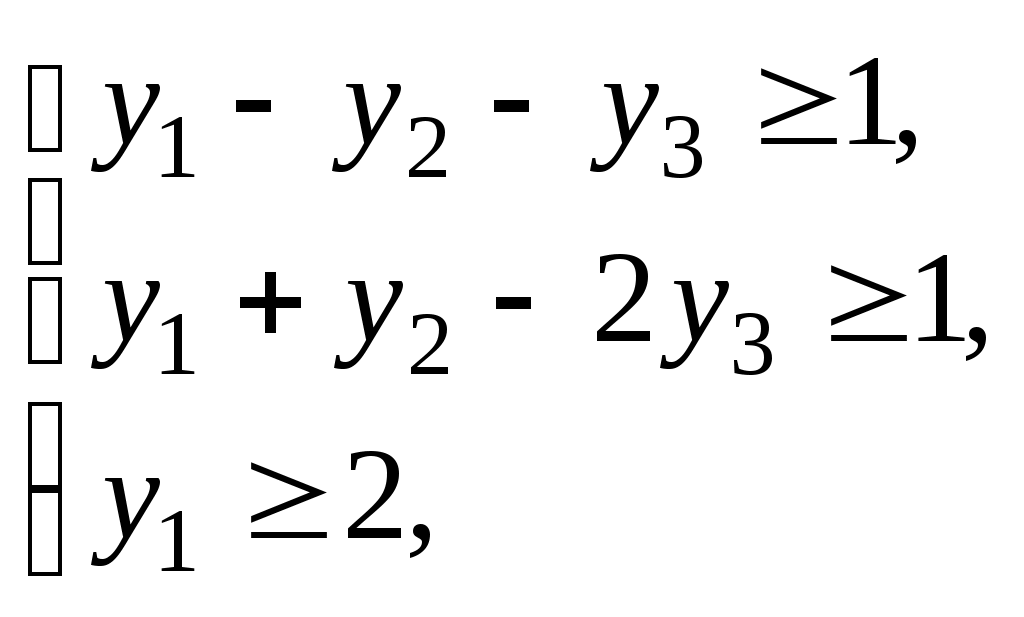 (61)
(61)Выбрав в качестве базиса векторы
Таблица 16
| i | Базис | Сб | Р0 | 1 | 1 | 2 | 0 | 0 |
| | | | | P1 | P2 | P3 | p4 | p5 |
| 1 2 3 4 | p3 P4 p5 | 2 0 0 | 8 -4 -6 16 | 1 -1 -1 1 | 1 1 -2 1 | 1 0 0 0 | 0 1 0 0 | 0 0 1 0 |
Из этой таблицы видим, что планом двойственной задачи (57) - (59) является
Значит, в базис вводим вектор P2. Переходим к новой симплекс-таблице (табл. 17).
Таблица 17
| i | Базис | Сб | Р0 | 1 | 1 | 2 | 0 | 0 |
| | | | | P1 | P2 | P3 | p4 | p5 |
| 1 2 3 4 | p3 P4 p2 | 2 0 1 | 5 -7 3 13 | 1/2 -3/2 1/2 1/2 | 0 0 1 0 | 1 0 0 0 | 0 1 0 0 | 1/2 1/2 -1/2 1/2 |
Из этой таблицы видно, что получен новый план двойственной задачи