Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc

При этом плане значение ее линейной формы равно Таким образом, с помощью алгоритма двойственного симплекс-метода произведен упорядоченный переход от одного плана двойственной задачи к другому.

Так как в столбце вектора Р₀ таблицы 17 стоит отрицательное число -7, то рассмотрим элементы 2-й строки. Среди этих чисел есть одно отрицательное -3/2. Если бы такое число отсутствовало, то исходная задача была бы неразрешима. В данном случая переходим к новой симплекс-таблице (табл. 18).

Таблица 18

i	Базис	Сб	Р0	1	1	2	0	0
				P1	P2	P3	p4	p5
1 2 3 4	p3 P1 p2	2 1 1	8/3 14/3 2/3 32/3	0 1 0 0	0 0 1 0	1 0 0 0	1/3 -2/3 1/3 1/3	2/3 -1/3 -1/3 2/3

Как видно из таблицы 18, найдены оптимальные планы исходной и двойственной задач. Ими являются и . При этих планах значения линейных форм исходной и двойственной задач равны:

---

1.17. Найти максимальное значение функции при условиях



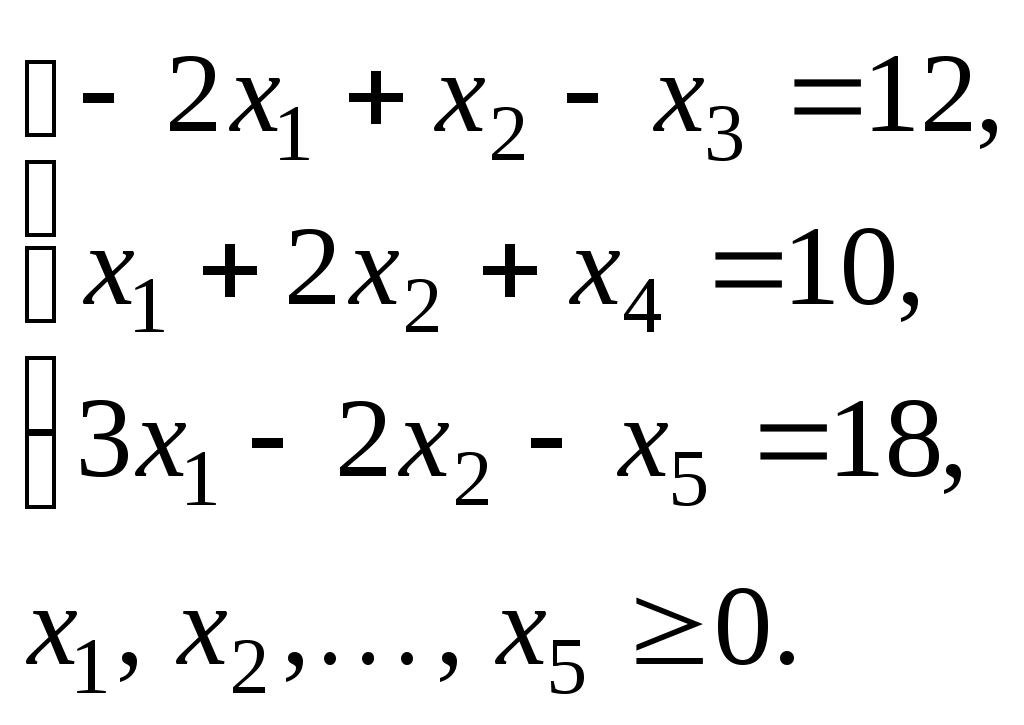
Решение. Умножая первое и третье уравнения системы ограничений задачи на -1, в результате приходим к задаче нахождения максимального значения функции при условиях



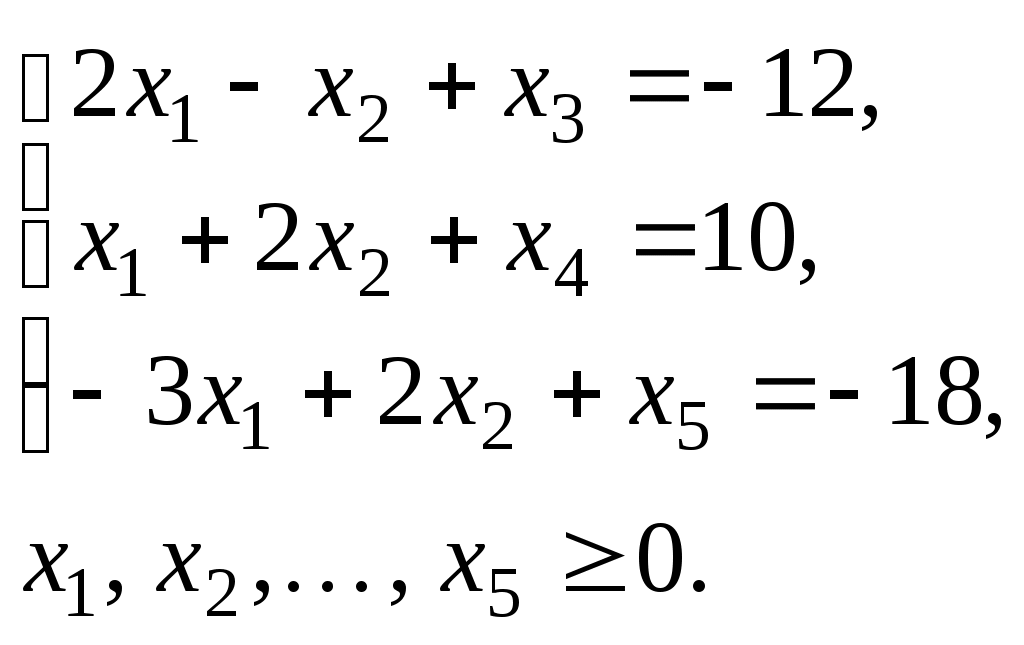
Взяв в качестве базиса векторы Р₃, Р₄ и Р₅, составляем симплекс-таблицу (табл. 19).

Таблица 19

i	Базис	Сб	Р0	2	3	0	5	0
				P1	P2	P3	p4	p5
1 2 3 4	p3 P4 p5	0 5 0	-12 10 -18 50	2 1 -3 3	-1 2 2 7	1 0 0 0	0 1 0 0	0 0 1 0

В 4-й строке таблице 19 нет отрицательных чисел. Следовательно, если бы в столбце вектора Р₀ не было отрицательных чисел, то в таблице 19 был бы записан оптимальный план. Поскольку в указанном столбце отрицательные числа имеются и такие же числа содержатся в соответствующих строках, переходим к новой симплекс-таблице (таблица 20). Для этого исключим из базиса вектор Р₅ и введем в базис вектор Р₁. В результате получим псевдоплан

---

Таблица 20

i	Базис	Сб	Р0	2	3	0	5	0
				P1	P2	P3	p4	p5
1 2 3 4	p3 P4 p1	0 5 2	-24 4 6 32	0 0 1 0	1/3 8/3 -2/3 9	1 0 0 0	0 1 0 0	2/3 1/3 -1/3 1

Так как в строке вектора Р₃ нет отрицательных чисел, то исходная задача не имеет решения.

Построение математических моделей. Решение задачи оптимального распределения ресурсов в среде EXCEL

Цель занятия: знакомство студентов с задачами линейного программирования.

Задачи занятия:

- изучение формы моделей задачи линейного программирования (ЗЛП);

- получение навыка решения ЗЛП в среде EXCEL
Методические указания

.






R=

---

В ячейке А1 введем целевую функцию, в ячейках С1-5 задавая неизвестные пока значения переменных целевой функции:

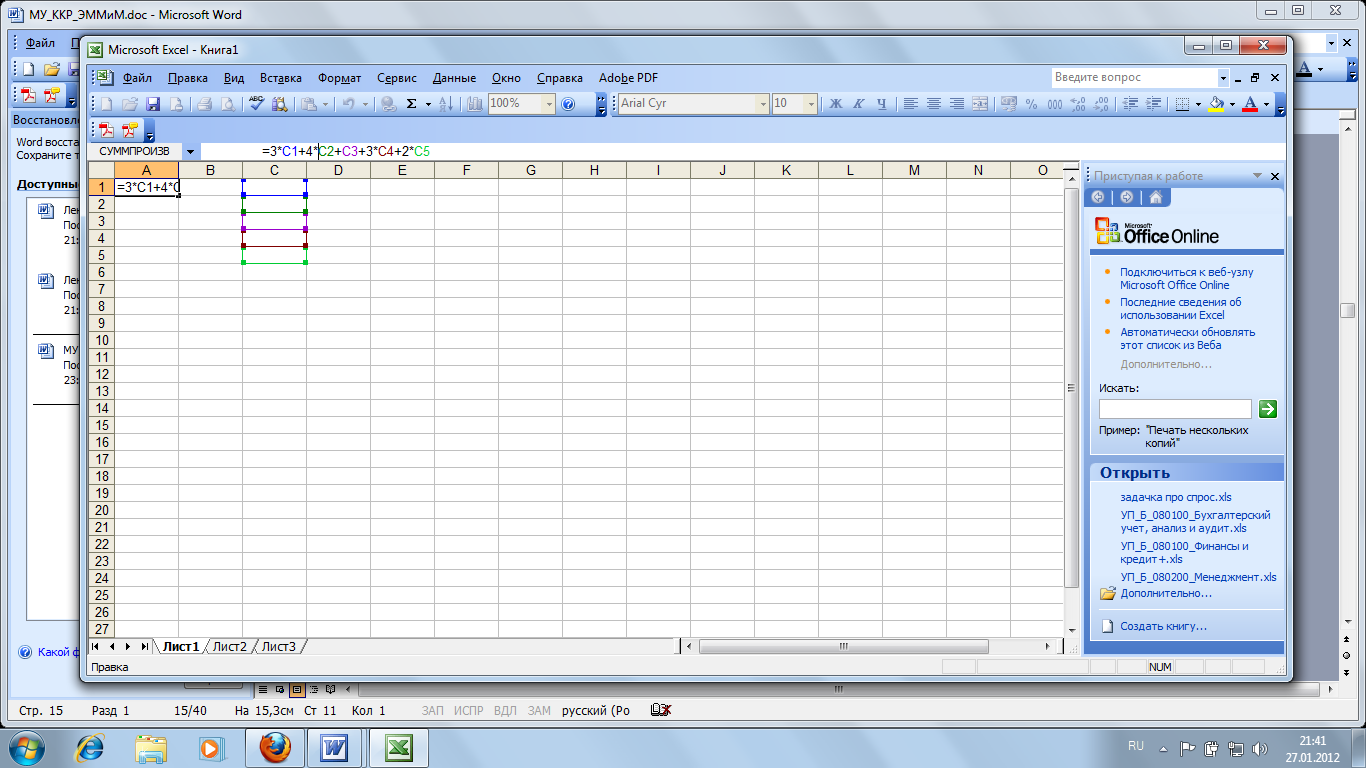
В ячейке В задаем левые части неравенств системы ограничений:

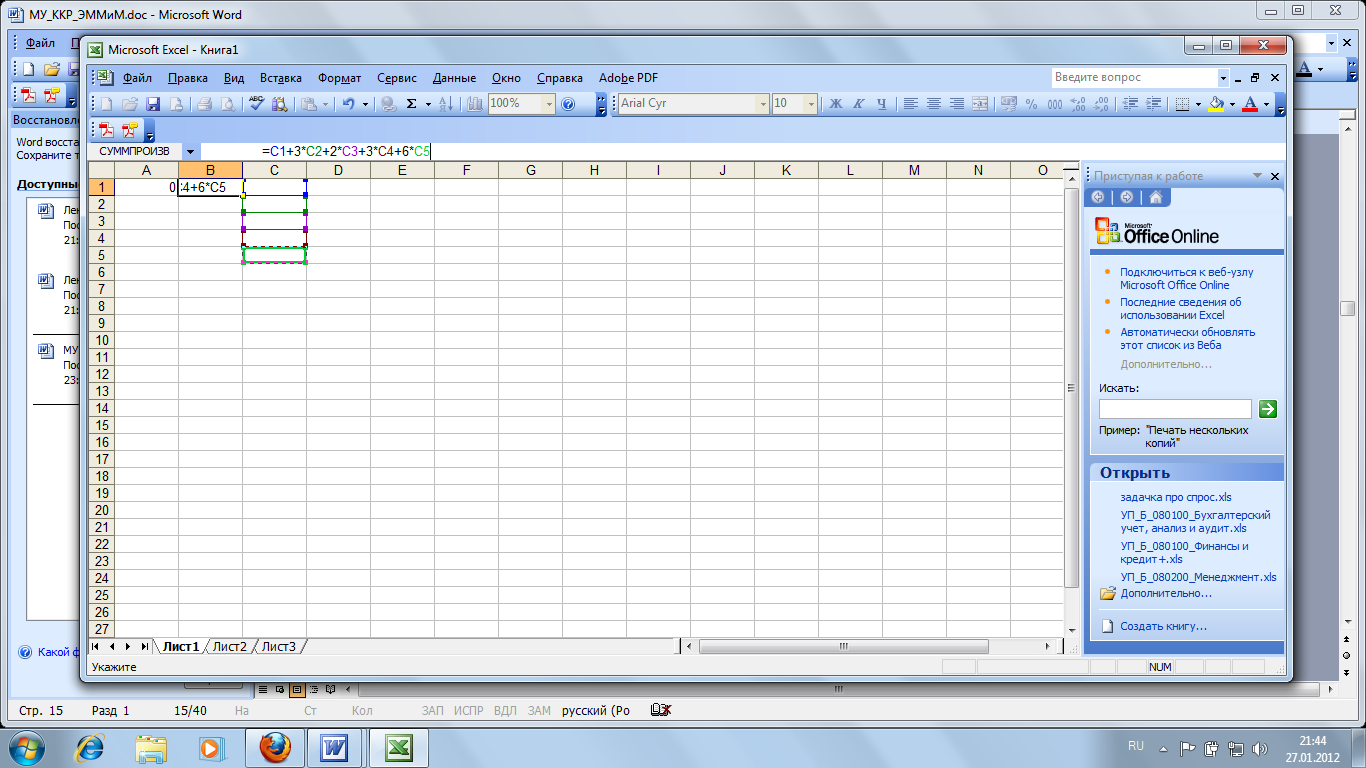
Через СЕРВИС/НАДСТРОЙКИ установить Поиск решения:

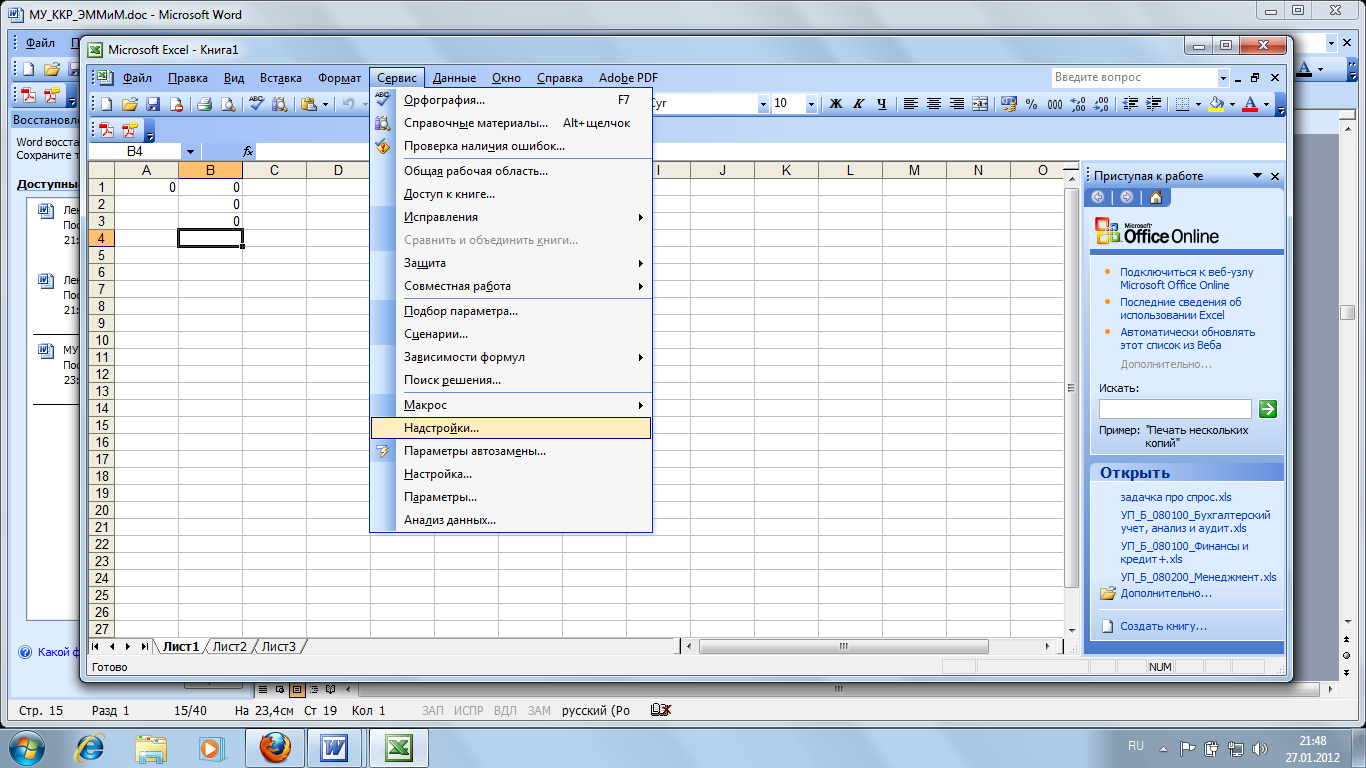
Через СЕРВИС/ПОИСК РЕШЕНИЯ открыть окно поиска решения и выбрать А1 целевой ячейкой:

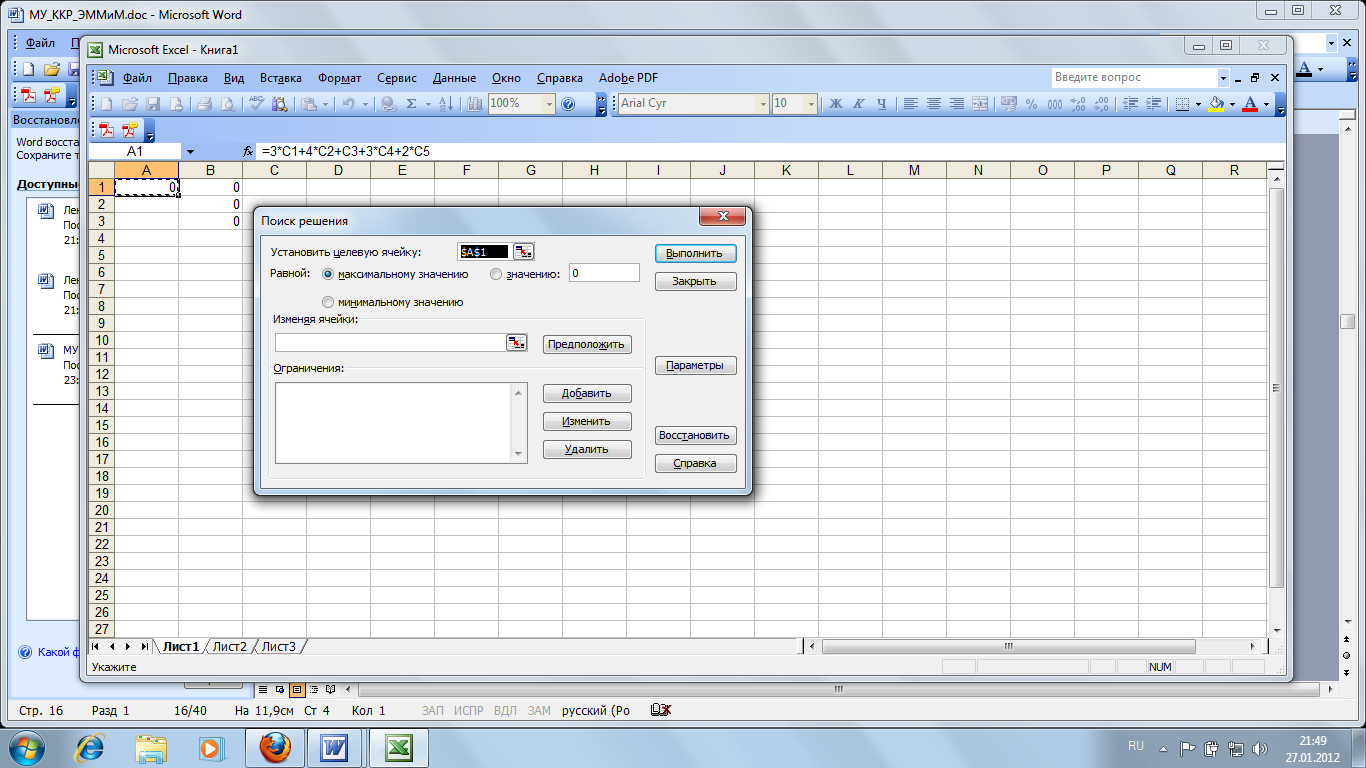
В окне «Изменяя ячейки» выбираем С1-С5 и вводим ограничения (кнопка ДОБАВИТЬ):

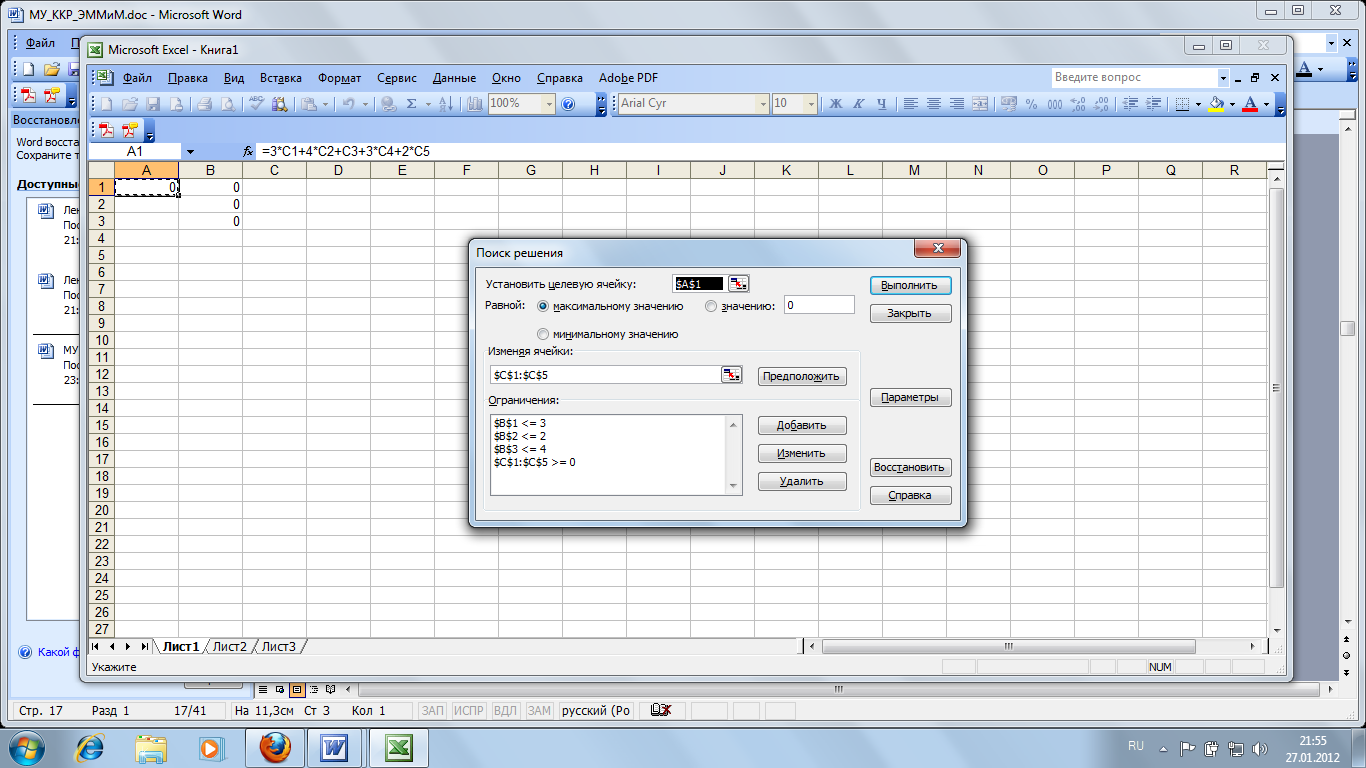
Нажав кнопку ВЫПОЛНИТЬ, получим решение:



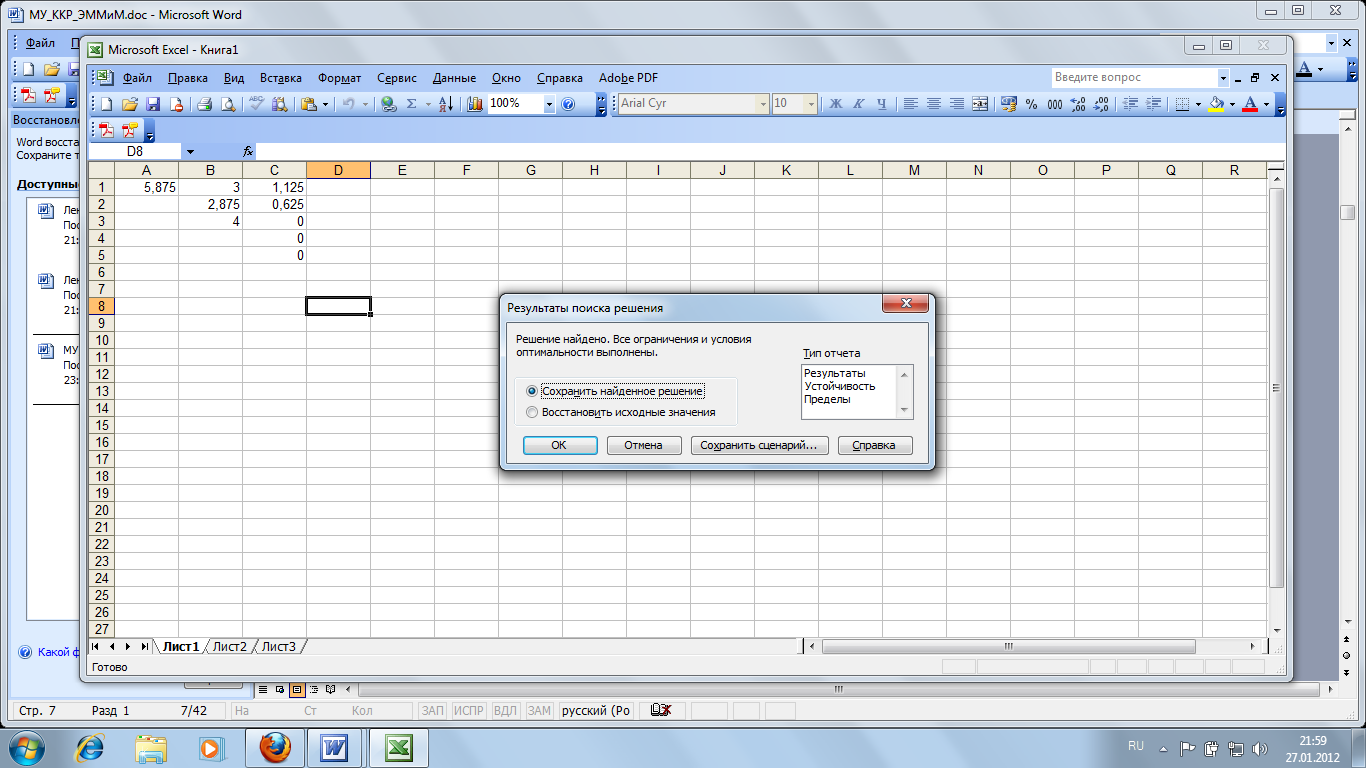
Графический метод решения ПЗЛП

Задачи:

- изучение алгоритма графического метода решения ЗЛП;

- получение практического навыка решения ЗЛП графическим методом.

Методические указания

Рассмотрим следующую задачу линейного программирования¹:





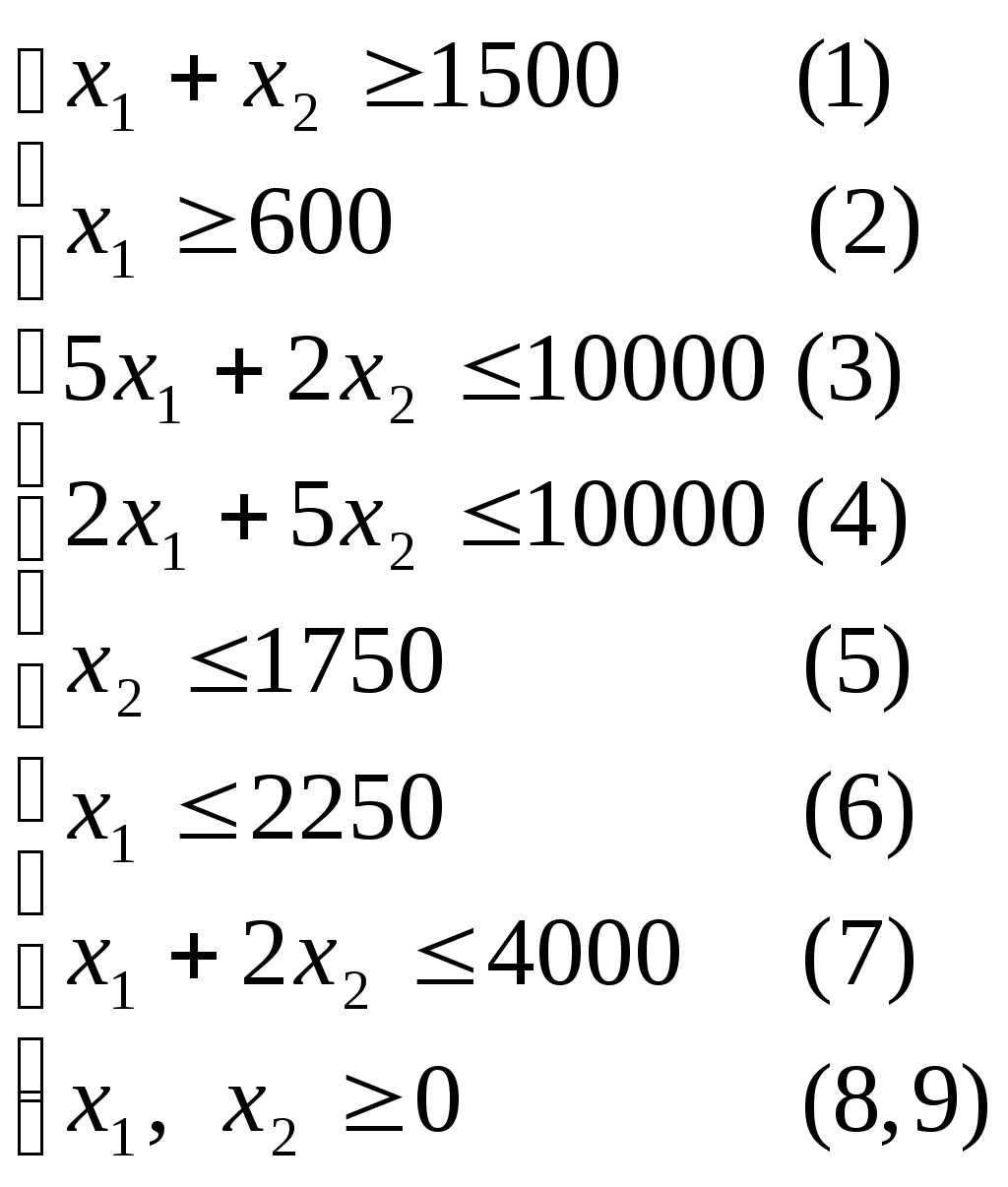
На рис. 4.1 представлено множество допустимых точек, удовлетворяющих всем ограничениям задачи и представляющее собой пересечение полуплоскостей, отражающих ограничения задачи линейного программирования.



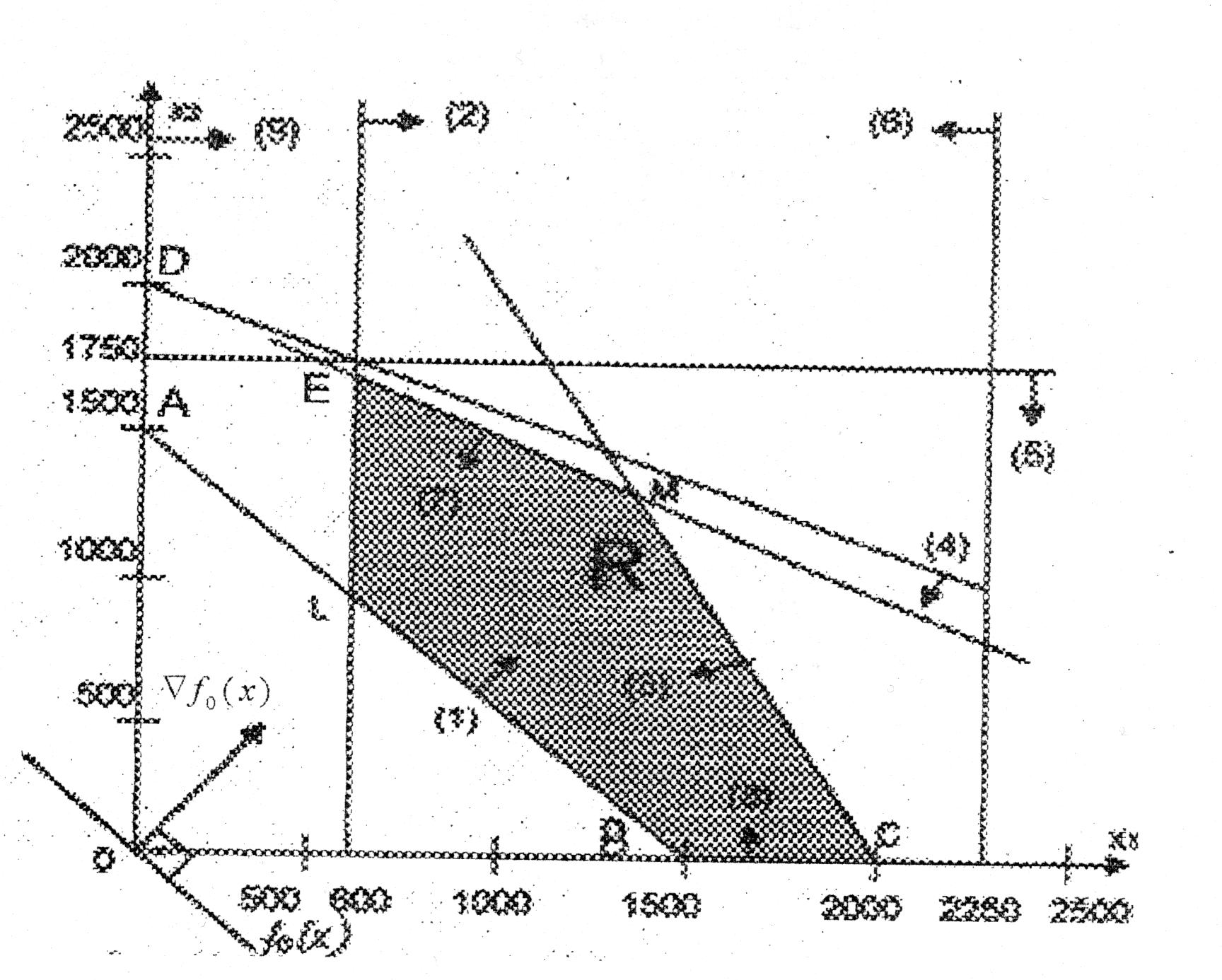
Рис. 4.1. Геометрическая интерпретация решения задачи
Геометрическую интерпретацию имеют ЗЛП с двумя переменными.

Исследуем целевую функцию 30х₁ + 40х₂. Данной целевой функции соответствует семейство прямых 30

---

х₁ + 40х₂ = L, представляющих собой множество параллельных прямых, каждая из которых соответствует определенному значению параметра L. Тогда задачу линейного программирования можно сформулировать следующим образом. Найти такое максимальное значение L, при котором прямая 30х₁ + 40х₂ = L пересекает допустимое множество.

В общем случае с геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на которой достигается самая верхняя (нижняя) линия уровня (прямая, отражающая целевую функцию), расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент целевой функции Ñf(`X) на плоскости Х₁ОХ₂. Этот вектор показывает направление наискорейшего изменения целевой функции, он равен

,

где и - единичные векторы по осям ОХ₁ и ОХ₂ соответственно. Таким образом, Ñf(`X) = (¶f/¶x<sub>1</sub>, (¶f/¶x<sub>2</sub>). Координатами вектора-градиента целевой функции Ñf(`X) являются коэффициенты целевой функции f(`X).

В рассматриваемом примере, если двигать прямую 30х₁ + 40х₂ = L из начала координат по направлению вектора-градиента целевой функции, то точкой, в которой достигается самая верхняя линия уровня является точка М пересечения прямых 5x₁ + 2x₂ = 1000 и x₁ + 2x₂ = 4000 с координатами x₁ = 1500 и x₂ = 1250. Таким образом, оптимальное решение достигается в точке М (1500; 1250). При этом значение целевой функции составит f(`X^*) =30 * 1500 + 40 * 1250 = 95000.

На этом примере можно увидеть основные свойства задач линейного программирования: допустимое множество точек представляет собой выпуклый многоугольник, получившийся в результате пересечения полуплоскостей и наибольшее значение целевой функции достигается в его вершине – крайней точке.

Решение задачи линейного программирования может быть не единственным, а состоять из бесконечного числа точек.

---