Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc

Экономическая интерпретация двойственных задач. Экономическую интерпретацию двойственных задач и двойственных оценок рассмотрим на примере.

1.15. Для производства трех видов изделий А, В и С используется три различных вида сырья. Каждый из видов сырья может быть использован в количестве, соответственно не большем 180, 210 и 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции каждого вида приведены в таблице 13.

Таблица 13

Вид сырья	Нормы затрат сырья (кг) на единицу продукции
	А	В	С
I II III	4 3 1	2 1 2	1 3 5
Цена единицы продукции (руб.)	10	14	12

Определить план выпуска продукции, при котором обеспечивается ее максимальная стоимость, и оценить каждый из видов сырья, используемых для производства продукции. Оценки, приписываемые каждому из видов сырья, должны быть такими, чтобы оценка всего используемого сырья была минимальной, а суммарная оценка сырья, используемого на производство единицы продукции каждого вида,— не меньше цены единицы продукции данного вида.

Решение. Предположим, что производится изделий А, изделий В и изделий С. Для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции

(48)

при следующих условиях

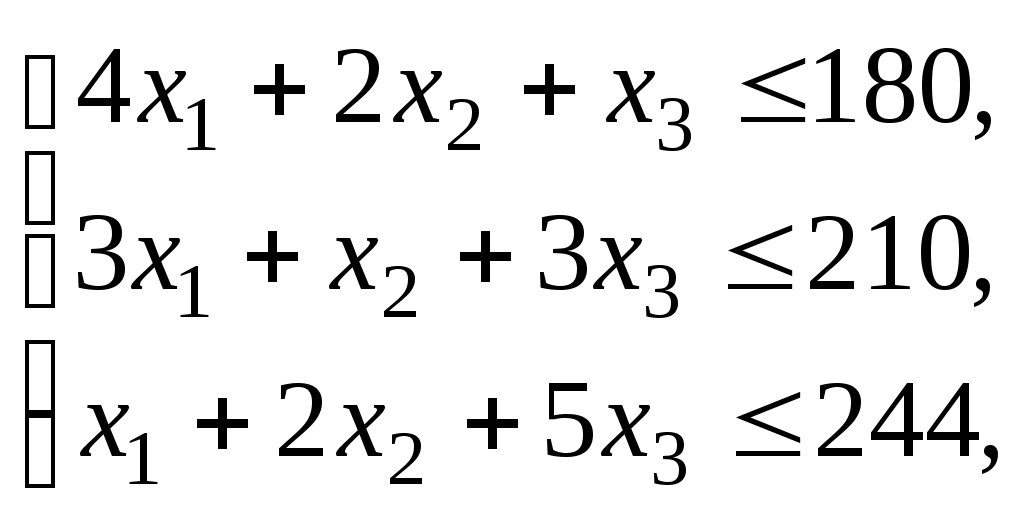(49)

(50)

Припишем каждому из видов сырья, используемых для производства продукции, двойственную оценку, соответственно равную

---

и у₃. Тогда общая оценка сырья, используемого на производство продукции, составит

(51)

Согласно условию, двойственные оценки должны быть такими, чтобы общая оценка сырья, используемого на производство единицы продукции каждого вида, была не меньше цены единицы продукции данного вида, т. е. и у₃ должны удовлетворять следующей системе неравенств:

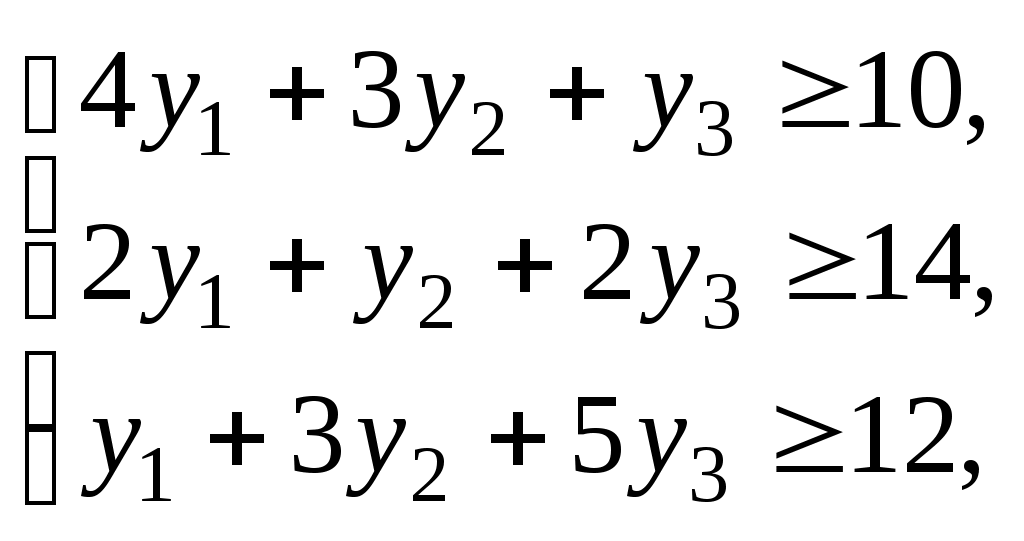(52)

(53)

Как видно, задачи (48) - (50) и (51) - (53) образуют симметричную пару двойственных задач. Решение прямой задачи дает оптимальный план производства изделий A, В и С, а решение двойственной — оптимальную систему оценок сырья, используемого для производства этих изделий. Чтобы найти решение этих задач, следует сначала отыскать решение какой-либо одной из них. Так как система ограничений задачи (48) - (50) содержит лишь неравенства вида «», то лучше сначала найти решение этой задачи. Ее решение приведено в таблице 14.

Из этой таблицы видно, что оптимальным планом производства изделий является такой, при котором изготовляется 82 изделия В и 16 изделий С. При данном плане производства остается неиспользованным 80 кг сырья II вида, а общая стоимость изделий равна 1340 руб. Из таблицы 14 также видно, что оптимальным решением двойственной задачи является

Таблица 14

i	Базис	Сб	Р0	10	14	12	0	0	0
				P1	P2	P3	p4	p5	Р6
1 2 3	p2 P5 p3	14 0 12	82 80 16 1340	19/8 23/8 -3/4 57/4	1 0 0 0	00 1 0	5/8 1/8 -1/4 23/4	0 1 0 0	-1/8 -5/8 1/4 5/4

---

Переменные и обозначают условные двойственные оценки единицы сырья, соответственно I и III видов. Эти оценки отличны от нуля, а сырье 1 и III видов полностью используется при оптимальном плане производства продукции. Двойственная оценка единицы сырья II вида равна нулю. Этот вид сырья не полностью используется при оптимальном плане производства продукции.

Таким образом, положительную двойственную оценку имеют лишь те виды сырья, которые полностью используются при оптимальном плане производства изделий. Поэтому двойственные оценки определяют дефицитность используемого предприятием сырья. Более того, величина данной двойственной оценки показывает, на сколько возрастает максимальное значение целевой функции прямой задачи при увеличении количества сырья соответствующего вида на 1 кг. Так, увеличение количества сырья I вида на 1 кг приведет к тому, что появится возможность найти новый оптимальный план производства изделий, при котором общая стоимость изготовляемой продукции возрастет на 5,75 руб. и станет равной 1340+5,75=1345,75 руб. При этом числа, стоящие в столбце вектора таблицы 14, показывают, что указанное увеличение общей стоимости изготовляемой продукции может быть достигнуто за счет увеличения выпуска изделий В на 5/8 ед. и сокращения выпуска изделий С на 1/4 ед. Вследствие этого использование сырья II вида уменьшится на 1/8 кг. Точно так же увеличение на 1 кг сырья III вида позволит найти новый оптимальный план производства изделий, при котором общая стоимость изготовляемой продукции возрастет на 1,25 руб. и составит 1340+1,25=1341,25 руб. Это будет достигнуто в результате увеличения выпуска изделий С на 1/4 ед. и уменьшения изготовления изделий В на 1/8 ед., причем объем используемого сырья II вида возрастет на 5/8 кг.

Продолжим рассмотрение оптимальных двойственных оценок. Вычисляя минимальное значение целевой функции двойственной задачи

видим, что оно совпадает с максимальным значением целевой функции исходной задачи.

При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получаем

---

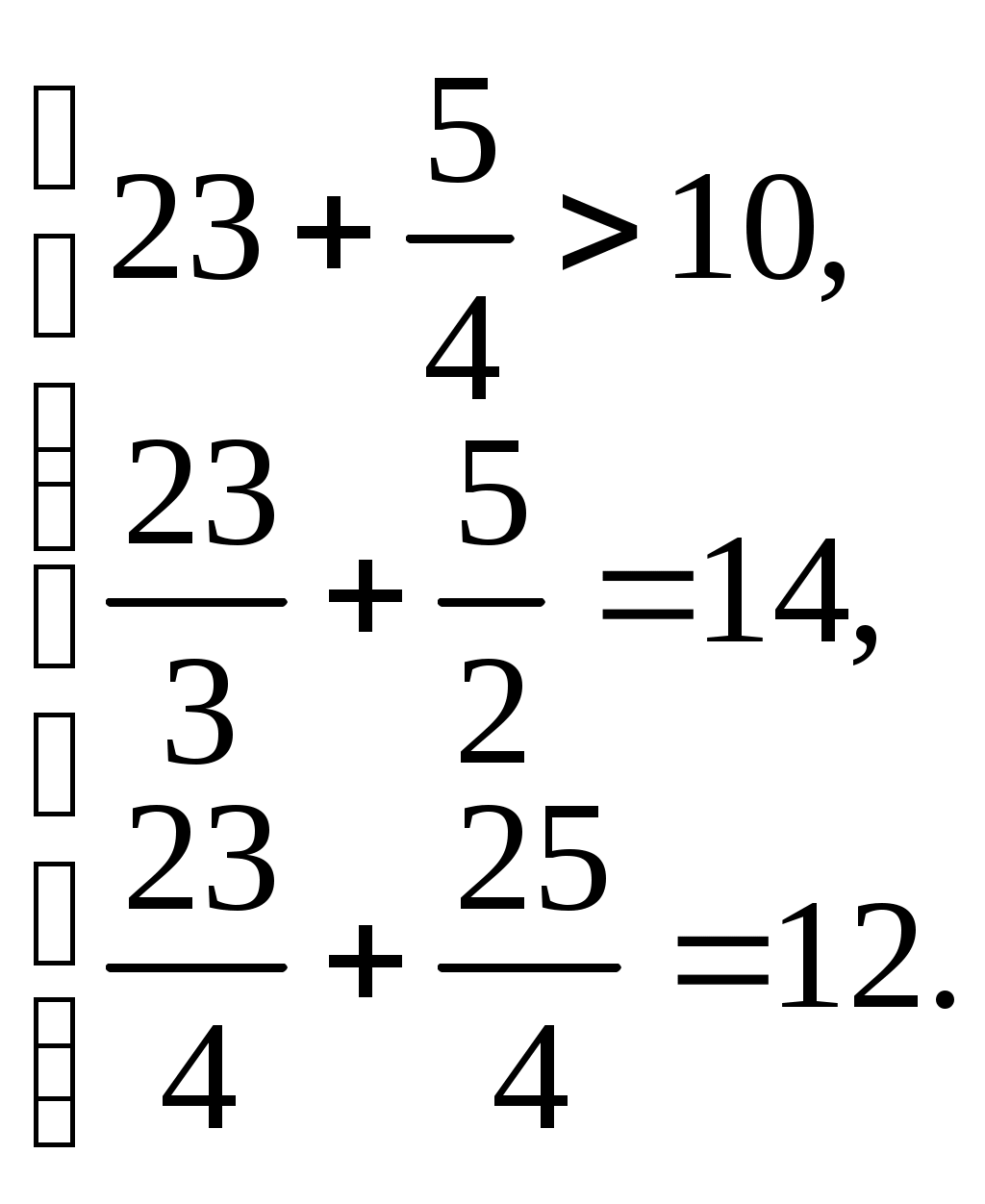
Первое ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственная оценка сырья, используемого на производство одного изделия вида А,выше цены этого изделия и, следовательно, выпускать изделия вида А невыгодно. Его производство и не предусмотрено оптимальным планом прямой задачи. Второе и третье ограничения двойственной задачи выполняются как строгие равенства. Это означает, что двойственные оценки сырья, используемого для производства единицы соответственно изделий В и С, равны в точности их ценам. Поэтому выпускать эти два вида продукции по двойственным оценкам экономически целесообразно. Их производство и предусмотрено оптимальным планом прямой задачи.

Таким образом, двойственные оценки тесным образом связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план, так и на систему оптимальных двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости. К рассмотрению этого мы сейчас и перейдем.

---

1.7. Двойственный симплекс-метод.

Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в форме основной задачи, для которой среди векторов ,составленных из коэффициентов при неизвестных в системе уравнений, имеется т единичных. Вместе с тем двойственный симплекс-метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательны ми). Такую задачу и рассмотрим теперь, предварительно предположив, что единичными являются векторы т. е. рассмотрим задачу, состоящую в определении максимального значения функции

(54)

при условиях

(55)

(56)

где



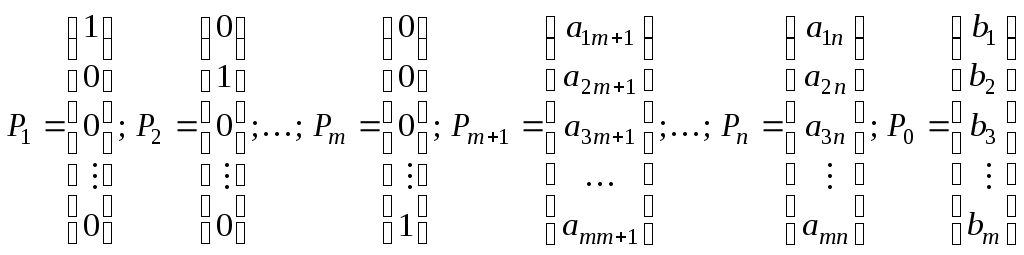
и среди чисел имеются отрицательные.

В данном случае есть решение системы линейных уравнений (55). Однако это решение не является планом задачи (54) - (56), так как среди его компонент имеются отрицательные числа.

Поскольку векторы — единичные, каждый из векторов можно представить в виде линейной комбинации данных векторов, причем коэффициентами разложения векторов по векторам

---