Файл: Бодалев А. А. Столин В. В.docx

X P F F* PR σ

2,1

3 2 2 1 1,6 -

4 18 20 11 17,7 -0,9

5 13 33 26,5 42,7 -0,2

6 8 41 37 59,7 0,2

7 10 51 46 74,2 0,6

8 6 57 54 87,1 1,1

Трудность, с которой сталкиваются начинающие при использовании интервальной нормализации, состоит в том, что обычные статистические таблицы не приспособлены для психометрики: нужно отыскивать значение процентильного ранга внутри таблицы, а соответствующую сигма-оценку – с краю. Для облегчения ориентации приведем фрагмент таблицы соответствий PR, а и стенов (табл. 4): Таблица 4

70

20

В обычных таблицах из соображений симметрии даны лишь значения для PR > 50. Для PR < 50 соответствующие значения находятся из тех же таблиц σ = ψ ^-1(1- PR/100). Например, для PR =35 мы находим 1 - PR/100 = 1 - 0,35 = 0,65, затем - по табл. ψ ^-1 = 0,39 и берем это значение с отрицательным знаком -0,39. Для нормализации удобно пользоваться графическим методом (нормальной бумагой, стандартной 5-образной кривой и т. п.).

В результате нормализации интервалы между исходными сыры-

ми баллами переоцениваются в соответствии с нормальной моделью. В отличие от процентильной шкалы, нормальная шкала придает больший вес (в дифференциации испытуемых) краям распределения: различия между испытуемыми, набравшими 95 и 90 процентилей, оцениваются как более высокие, чем различия между испытуемыми, набравшими 65 и 60 процентилей.

В применении к шкалам оценок (рейтинговым шкалам) метод нормализации интервалов называется «методом последовательных интервалов» (Клигер С. А. и др., 1978, с. 75-81).

В результате применения процедуры нормализации исследователь-психометрист получает для нормативной выборки таблицу перевода сырых баллов в нормализованные баллы. На основе этих таблиц часто строят графики: деления сырых баллов наносят на числовую ось с неравными интервалами, так что эмпирическое распределение частот максимально близко приближается к нормальной форме. Пример такой графической нормализации - профильные листы MMPI (Анастази А., 1982, с. 129).

---

Так как нормальное распределение описывается всего двумя параметрами: средним М (мерой положения) и средним квадратическим (или стандартным) отклонением а (мерой рассеяния), то диагностические нормы в случае нормализованных шкал описываются в единицах отклонений от среднего по выборке; например, заключают, что испытуемый А показал результат, превышающий средний балл на две сигмы, испытуемый В -результат, оказавшийся ниже среднего балла на одну сигму, и т. п. На процентильной шкале этому соответствуют процентильные ранги 95 и 16 соответственно.

Переход к нормальному распределению создает очень удобные условия для количественных операций с диагностической шкалой: как со шкалой интервалов с ней можно производить операции линейного преобразования (умножение и сложение), можно описывать диагностические нормы в компактной форме (в единицах отклонений), можно применять линейный коэффициент корреляции Пирсона, критерии для проверки статистических гипотез, построенные в применении к нормальному распределению, т. е. весь аппарат традиционной статистики (основанной на нормальном распределении). !

Неправомерность онтологизации нормального закона. В традиционной психометрике нормальное распределение выступает в роли инструментального понятия, облегчающего оперирование с данными. Но это не означает, что можно забывать об искусственном происхождении нормального распределения. Традиции западной тестологии, основанные еще Ф. Гальтоном, предполагают однородность теоретических представлений психометрики и биометрики. Точно так же как происхождение нормального распределения при исследовании вариативности биологических характеристик человеческого организма связывается с наличием взаимодействия постоянного фактора генотипа и изменчивых случайных факторов фенотипа, - происхождение межиндивидуальных психологических различий связывается с генетическим кодом, якобы предопределяющим положение индивида на оси нормальной кривой. В действительности же нет никаких оснований приписывать появление нормальной кривой, часто получаемой с помощью специальных статистических непростых процедур, действию механизма наследственности.

В тех случаях, когда на большой выборке удается получить нормальное распределение без каких-либо искусственных способствующих этому мер

---

, это опять-таки не означает вмешательства генетики. Закон нормального распределения воспроизводится всякий раз, когда на измеряемое свойство (на формирование определенного уровня способностей индивида) действует множество разных по силе и направленности факторов, независимых друг от друга. История прижизненных средовых воздействий, которые испытывает на себе субъект, также подобна последовательности независимых событий: одни факторы действуют в благоприятном направлении, другие - в неблагоприятном, а в результате взаимопогащение их влияний происходит чаще, чем тенденциозное однонаправленное сочетание (большинство благоприятных или большинство неблагоприятных), т. е. возникает нормальное распределение. Массовые исследования показывают, что введение контроля над одним из средовых популяционных факторов (уровень образования родителей, например) приводит к расслоению кривой нормального распределения: выборочные кривые оказываются смещенными относительно друг друга (Анастази А., 1982, с. 201). Эти результаты служат ярким подтверждением социокультурного происхождения статистических диагностических норм, что одновременно служит основанием для серьезных предосторожностей при переносе норм, полученных на одной популяции, на другие популяции. Однородными можно считать только те популяции, по отношению к которым действует одинаковый механизм выборки: ив ситуации создания (стандартизации) теста, и в ситуации его диагностического применения. Здесь приходится учитывать и такие нюансы выборочного механизма, как феномен нормальных добровольцев. Если выборку стандартизации формировать на студентах, добровольно согласившихся участвовать в тестировании, а применение теста планируется на сплошных выборках (в административном порядке), то это грозит определенными ошибками в диагностических суждениях, так как психологический портрет «добровольца» в существенных чертах отличается от портрета испытуемого, соглашающегося на тестирование только под административным давлением (Шихирев П.Н, 1979, с. 181).

Подсчет параметров и оценка типа распределения. Для описания выборочного распределения, как правило, используются следующие известные параметры:

1. 
   Среднее арифметическое значение:
   

n

1

x p_j y_j , (3.1.1) n j1

где x_j – балл i-го испытуемого;

y_i -значение i-го балла по порядку возрастания; p

---

_i - частота встречающегося i-го балла; n - количество испытуемых в выборке (объем); m - количество градаций шкалы (количество баллов).

2. 
   Среднее квадратическое (стандартное) отклонение:
   

3.

s 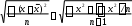 , (3.1.2)

где x² - сумма квадратов тестовых баллов для и испытуемых.

3. 
   Асимметрия:
   
   1. 
      ^{2 3}
      

AS  3  3C x  2x  S

(3.1.3)



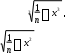
где x - среднее арифметическое значение; S - стандартное отклонение; θ - среднее кубическое значение: 

С - среднее квадратическое: C 

4. 
   Эксцесс:
   
   1. 
       ^{4 3 2 2 4}
      

Ex^ 4 Q 40 x6C x 3x 3, (3.1.4) s

1 ⁴

где Q - среднее значение четвертой степени: Q⁴ x . n

Стандартная ошибка среднего арифметического значения (математического ожидания) оценивается по формуле:

s

s_m 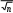 (3.1.5)

На основе ошибки математического ожидания строятся довери-

тельные интервалы: (x  2S_m ; x  2S_m )

Если тестовый балл какого-либо испытуемого попадает в границы доверительного интервала, то нельзя считать, что испытуемый обладает повышенным (или пониженным) значением измеряемого свойства с заданным уровнем статистической значимости.

Асимметрия и эксцесс нормального распределения должны быть равны нулю. Если хотя бы один из двух параметров существенно отличается от нуля, то это означает анормальность полученного эмпирического распределения.

Проверку значимости асимметрии можно произвести на основе общего неравенства Чебышева:

---

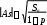(3.1.6)

где S_a - дисперсия эмпирической оценки асимметрии:

^S_a ^ , (3.1.7)

где р - уровень значимости или вероятность ошибки первого ро-

да: ошибки в том, что будет принят вывод о незначимости асимметрии при наличии значимой асимметрии (в формулу подставляют стандартные р = 0,05 или р = 0,01 и проверяют выполнение неравенства).

Сходным образом оценивается значимость эксцесса:

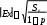(3.1.8)

где S_е - эмпирическая дисперсия оценки эксцесса:

S_e  . (3.1.9)

]

Гипотезы об отсутствии асимметрии и эксцесса принимаются с вероятностью ошибки р (пренебрежимо малой), если выполняются неравенства (3.1.6) и (3.1.8).

Более легкий метод проверки нормальности эмпирического распределения основывается на универсальном критерии Колмогорова. Для каждого тестового балла у. (для каждого интервала равнозначности при дискретизации непрерывной хронометрической шкалы) вычисляется величина D. - модуль отклонения эмпирической и теоретической интегральных функций распределения:

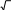
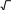
D _j  F(y _j ) U(z _j) (3.1.10) где F- эмпирическая интегральная функция (значение кумуляты в данной точке у_j); U — теоретическая интегральная функция, взятая из таблиц⁷. Среди D_j отыскивается максимальное значение D_max n , и величина _e D_max n сравнивается с табличным значением _t критерия Колмогорова.

В таблице 5 приведены асимптотические критические значения для распределения Колмогорова (при n  ). Близость эмпирического значения λ_е к левосторонним стандартным квантилям λ_t позволяет констатировать близость эмпирического и предполагаемого теоретического распределения с пренебрежимо малой вероятностью ошибки р (0,01; 0,05; 0,10 и т, п.). Близость λ_е к правосторонним стандартным квантилям λ_t позволяет сделать вывод о статистически значимом отсутствии согласованности эмпирического и теоретического распределений. Надо помнить, что критерий Колмогорова, очень простой в вычислительном' отношении, обеспечивает надежные выводы лишь при

---