Файл: Бодалев А. А. Столин В. В.docx

Несколько раньше была получена формула Кьюдера - Ричардсона, аналогичная формуле Кронбаха для частного случая - когда ответы на каждый пункт теста интерпретируются как дихотомические переменные с двумя значениями (1 и 0):

 2 k 

 S _x  p _j q _j  k  j_1 

KR₂₀  k 1^ _Sx2 ^_ (3.2.9)

 

где KR₂₀ - традиционное обозначение получаемого коэффициен-

та;

p _jq _j -дисперсия i-и дихотомической переменной, какой является

N(«верно»)

i-й пункт теста; р = , q = 1 - p n

В 1957 г. Дж. Ките предложил следующий критерий для оценки статистической значимости коэффициента a:

где X _n²_1 - эмпирическое значение статистики % квадрат с п-1 степенью свободы; k - количество пунктов теста; n - количество испытуемых;. a - надежность.

Формулы (3.2.8) и (3.2.9) позволяют оценить взаимную согласованность пунктов теста, используя при этом только подсчет дисперсий. Однако коэффициенты а и KR_2I> позволяют оценить и среднюю корреляцию между i-м и j-м произвольными пунктами теста, так как связаны с этой средней корреляцией следующей формулой:

a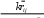^ 11)

1(k1)r_ij



где ^r_ij - средняя корреляция между пунктами теста. Легко увидеть идентичность формулы (3.2.11) обобщенной формуле Спирмена - Брауна, позволяющей прогнозировать повышения синхронной надежности теста с увеличением количества пунктов теста в k раз (Аванесов В. С., 1982, с. 121). Из этой формулы видно, что при больших k малое значение r_ij может сочетаться с высокой надежностью. Пусть r_ij = 0,1, a k =100, тогда по формуле (3.2.11)

a   0,91

Широкое распространение компьютерных программ факторного анализа для исследования взаимоотношений между пунктами теста (по одномоментным данным) привело к обоснованию еще одной достаточно эффективной формулы надежности теста, которой легко воспользоваться, получив стандартную распечатку компьютерных результатов факторного анализа по методу главных компонент:

---

k  1 

k ^1_1 ^_ (3.2.12)

_1

где θ - коэффициент, получивший название тета-надежности

теста; k - количество пунктов теста;

λ₁ - наибольшее значение характеристического корня матрицы интеркорреляций пунктов (наибольшее собственное значение,

или абсолютный вес первой главной компоненты).

Как и предыдущие формулы, формула (3.2.12) также относится к оценке надежности теста, направленного на измерение одной характеристики. Но, кроме того, она применима и для многофакторного теста, хотя и нуждается в пересчете после первоначального отбора пунктов, релевантных фактору (после того, как на основании многофакторного анализа отобраны пункты по одному фактору, снова проводится факторный анализ - только для этих отобранных пунктов).

Надежность отдельных пунктов теста. Надежность теста обеспечивается надежностью пунктов, из которых он состоит. Чтобы повысить ретестовую надежность теста в целом, надо отобрать из исходного набора пунктов, апробируемых в пилотажных психометрических экспериментах, такие пункты, на которые испытуемые дают устойчивые ответы. Для дихотомических пунктов (типа «решил - не решил», «да - нет») устойчивость удобно измерять с использованием четырехклеточной матрицы сопряженности:

Тест 1

Да Нет

a	B
c	D

Да Тест 2

Нет

Здесь в клеточке а суммируются ответы «Да», данные испытуемым при первом и втором тестировании, в клеточке b - число случаев, когда испытуемый при первом тестировании отвечал «Да», а при втором - «Нет» и т. д. В качестве меры корреляции вычисляется фикоэффициент:

ad  bc

 (3.2.13)

(a  b)(c  d)(a  c)(b  d)

Как известно, значимость фи-коэффициента определяется с по мощью критерия хи-квадрат:

X₁² ² n (3.2.14)

Если вычисленное значение хи-квадрат выше табличного с одной степенью свободы, то нулевая гипотеза (о нулевой устойчивости) отвергается. Удобство использования фи-коэффициента состоит в том, что он одновременно оценивает степень оптимальности данного пункта теста по силе (трудности): фи-коэффициент оказывается тем меньшим, чем сильнее частота ответов «да» отличается от частоты ответа «нет».

---

Кроме того, сама четырехклеточная матрица позволяет проследить возможную несимметричность в устойчивости ответов «да» и «нет» (это важнее для задач, чем для вопросов: например, может оказаться, что все испытуемые, уже решившие однажды данную задачу, решают ее при повторном тестировании; это наводит на мысль о том, что при втором тестировании происходит сбережение опыта, приобретенного при первом тестировании). Выявленные в результате такого анализа неустойчивые и неинформативные (слишком сильные или слишком слабые) пункты должны быть исключены из теста. Пункты следует считать недостаточно устойчивыми, если на репрезентативной выборке величина 1превышает 0,71. При этом φ< 0,5.

Для т9. В отсутствие компьютера согласованность для пунктов также очень просто определяется с помощью четырехклеточной матрицы. В этом случае в первом столбце суммируются ответы испытуемых из «высокой».группы (пр величине суммарного балла), во втором столбце - из «низкой».

Высокая Низкая

A	B
C	D

Да

Нет

При нормальном распределении частот суммарных баллов «высокая» и «низкая» группы отсекаются справа и слева 27%-ными маргинальными квантилями (рис. 8).

Для оценки согласованности с суммарным баллом применяется полная¹⁰ или упрощенная формула фи-коэффициента:

2aP¹ 1

^i  (3.2.15)¹¹

P_i (N*P_i )

где P_i - количество ответов «верно» («да») на i-й пункт теста;

N* - сумма всех элементов матрицы;

N* = n • 0,54 где n - объём выборки;

P_i = а + b - При включении в эстремальную группу 1/3 выборки N* = 0,66 • n.



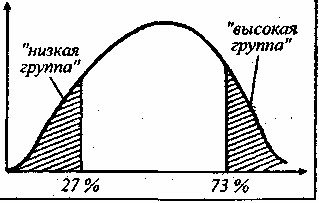
Рис. 8. Квантили «высокой» и «низкой» группы на графике распределения тестовых баллов

---

В некоторых случаях подобный анализ позволяет уточнить ключ для пункта: если пункт получает значимый положительный фи-коэффициент, то ключ определяется значением «+1», если пункт получает значимый отрицательный фи-коэффициент значением «-1». Если пункт получает незначимый фи-коэфф.ициент, то его целесообразно исключить из теста.

При ручных вычислениях фи-коэффициента удобно вначале с помощью формул (3.2.14) и (3.2.15) определить граничное значение значимого (по модулю) фи-коэффициента. Например, при объеме выборки в 100 человек и уровне значимости р < 0,01 пороговое значение вычисляется так:

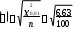 0.27 (3.2.16)

При постоянном использовании компьютера при подсчете суммарных баллов ключ для каждого пункта Q целесообразно определить в виде самого фи-коэффициента (или другого коэффициента корреляции), определенного при коррелировании ответов на пункт с суммарным баллом. Тогда тестовый балл подсчитывается по формуле

k

x_i R_ijC_j, (3.2.17)

j1

где х_i — суммарный балл i-го испытуемого;

^R_ij- ответ «верно» (+1) или «неверно» (-1) i-го испытуемого на i-й пункт;

С_i- ключ для i-го пункта: С = +1 для прямого, С= -1 для обратного.

Более чувствительный коэффициент, который также применяется для дихотомических пунктов, - это точечный бисериальный коэффициент корреляции, учитывающий амплитуду отклонения индивидуальных суммарных баллов от среднего балла:

1 n

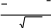ⁿ  x * p_i x 3.2.18)

r_pbi 

S x pi qi

где x* - сумма финальных баллов тех индивидов, которые дали утвердительный ответ на i-й пункт теста (решили i-ю задачу);

S_x - стандартное отклонение для суммарных баллов всех индивидов из выборки; pq - стандартное отклонение по i-му пункту; x - средний балл по всем пунктам.

А. Анастази относит критерий внутренней согласованности теста к валидности (Анастази А., 1982, кн. 1, с. 143), однако если и можно в данном случае говорить о валидности, то только в смысле особой внутренней валидности теста. Как правило, слишком высокая согласованность снижает внешнюю валидность теста по критерию (см. раздел 3.3). Если проверяется согласованность пунктов, составленных одним автором (одним коллективом по стандартной инструкции), то выявление достаточного набора согласованных пунктов свидетельствует о внутренней валидности (согласованности) разработанного диагностического понятия (конструкта).

---

В компьютерных данных факторного анализа аналогом корреляции пункта с суммарным баллом является нагрузка пункта на ведущий фактор («факторная валидность» в терминах А. Анастази). Если прибегать к геометрическому изображению нагрузки как проекции вектора-пункта на ось-фактор, то структура пунктов хорошо согласованного теста предстанет в виде пучка векторов, плотно прилегающих к фактору и вытянувшихся вдоль его оси (рис. 9).



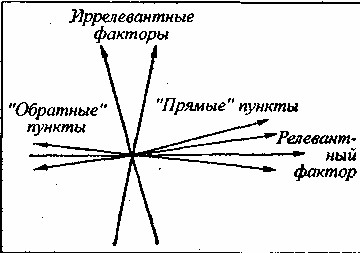
Рис. 9. Векторная модель соотношения «прямых» и «обратных» эмпирических пунктов с релевантным (измеряемым) фактором и иррелевантными («шумовыми») факторами

Последовательность действий при проверке надежности:

1. 
   Узнать, существуют ли данные о надежности теста, предполагаемого к использованию, на какой популяции и в какой диагностической ситуации проводилась проверка. Если проверки не было или признаки новых популяции и ситуации явно специфичны, провести заново проверку надежности с учетом указанных ниже возможностей.
   
2. 
   Произвести повторное тестирование на всей выборке стандартизации и подсчитать все коэффициенты, как для целого теста, так и для его отдельных пунктов. Анализ полученных коэффициентов позволит понять, насколько пренебрежима ошибка измерения, дает ли данный тест интервальную шкалу (высокий r) или только диагностичен для крайних групп (высокий φ), насколько устойчиво измеряемое свойство во времени (возможен ли статистический прогноз - проекция тестового балла на будущее), в каких своих пунктах тест менее надежен (анализ этих пунктов позволяет психологически осмыслить содержательный механизм взаимодействия пунктов с испытуемыми).
   
3. 
   Если возможности обследования испытуемых ограниченны, произвести повторное тестирование только на части выборки (не менее 30 испытуемых), подсчитать (вручную) ранговую или четырехклеточную корреляцию для оценки внутренней согласованности и стабильности теста в целом.
   

---