Файл: 1 Определение линейного пространства. Следствия из аксиом. Линейное пространство.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 124
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теорема 1. Корневое подпространство
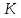 раскладывается в прямую сумму инвариантных подпространств, циклических относительно оператора B.
раскладывается в прямую сумму инвариантных подпространств, циклических относительно оператора B.В соответствии с теоремой 1
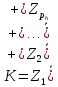 , где базисом циклического подпространства
, где базисом циклического подпространства 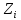 являются вектора
являются вектора 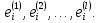 При этом имеет место
При этом имеет место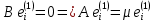
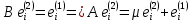
……………….
50) Жорданова нормальная форма матрицы линейного оператора
Рассмотрим линейный оператор
 , действующий в линейном пространстве
, действующий в линейном пространстве  над полем
над полем 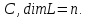 Пусть
Пусть 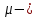 собственное число оператора
собственное число оператора  , а
, а 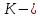 соответствующее ему корневое подпространство.
соответствующее ему корневое подпространство.Рассмотрим линейный оператор
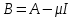 .
.Теорема 1. Корневое подпространство
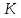 раскладывается в прямую сумму инвариантных подпространств, циклических относительно оператора B.
раскладывается в прямую сумму инвариантных подпространств, циклических относительно оператора B.В соответствии с теоремой 1
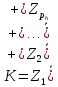 , где базисом циклического подпространства
, где базисом циклического подпространства 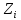 являются вектора
являются вектора 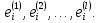 При этом имеет место
При этом имеет место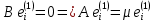
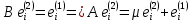
……………….
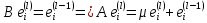 .
.Матрица индуцированного оператора
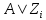 в указанном базисе имеет вид
в указанном базисе имеет вид

Матрицу
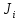 называют клеткой Жордана.
называют клеткой Жордана.В базисе
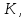 полученном в результате объединения базисов циклических подпространств, матрица линейного оператора имеет вид
полученном в результате объединения базисов циклических подпространств, матрица линейного оператора имеет вид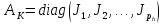 .
.Если разложить все пространство
 в прямую сумму корневых подпространств, а их в свою очередь разложить в прямую сумму циклических подпространств, то получим жорданову нормальную форму матрицы линейного оператора
в прямую сумму корневых подпространств, а их в свою очередь разложить в прямую сумму циклических подпространств, то получим жорданову нормальную форму матрицы линейного оператора  Она представляет собой блочно-диагональную матрицу с клетками Жордана на диагонали.
Она представляет собой блочно-диагональную матрицу с клетками Жордана на диагонали.Базис, в котором матрица оператора имеет ЖНФ, называют каноническим базисом.
51) Алгоритм построения канонического базиса (ну и ЖНФ)
Пример. Построить жорданову нормальную форму матрицы
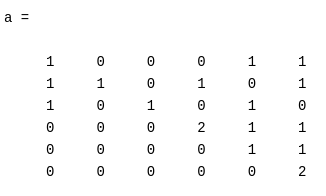
Матрица блочно-треугольная, характеристический многочлен имеет вид
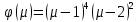
Таким образом, все пространство
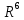 раскладывается в прямую сумму двух корневых подпространств
раскладывается в прямую сумму двух корневых подпространств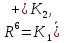
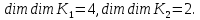
Рассмотрим собственное число
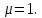
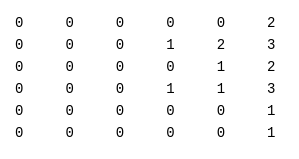
В=А-Е=

Решаем систему B
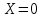 и находим базис собственного подпространства, соответствующего собственному числу 1.
и находим базис собственного подпространства, соответствующего собственному числу 1.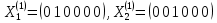
Геометрическая кратность собственного числа 1 равна 2, следовательно, корневое подпространство
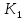 разлагается в прямую сумму двух циклических подпространств
разлагается в прямую сумму двух циклических подпространств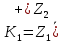
Первый этаж исходной таблицы состоит из двух векторов
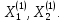
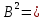
Находим фундаментальную систему решений
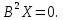
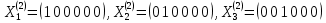
Корневым вектором высоты 2 является только
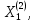 его и помещаем на второй этаж исходной таблицы.
его и помещаем на второй этаж исходной таблицы.
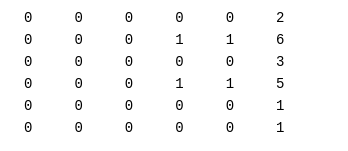 a
a Решая систему
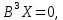 находим корневой вектор высоты 3 и помещаем его на третий этаж
находим корневой вектор высоты 3 и помещаем его на третий этаж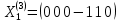
Исходная таблица для
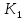 имеет вид
имеет вид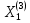
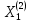
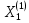
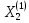
Для построения канонического базиса
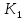 умножаем вектора таблицы, начиная с верхнего этажа, на матрицу
умножаем вектора таблицы, начиная с верхнего этажа, на матрицу 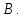
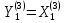
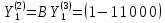 ,
, 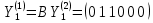 ,
, 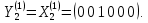
Канонический базис
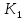
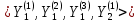
Перейдем к корневому подпространству
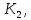 соответствующему собственному числу 2.
соответствующему собственному числу 2.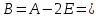

Базис собственного подпространства образует вектор
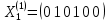
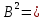

Фундаментальная система решений
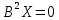 имеет вид
имеет вид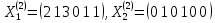
Корневым вектором высоты 2 является
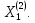 Исходная таблица
Исходная таблица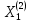
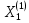
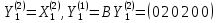
Канонический базис
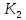
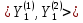 .
.Канонический базис
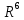 получим в результате объединения канонических базисов корневых подпространств
получим в результате объединения канонических базисов корневых подпространств 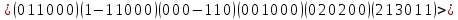
Жорданова нормальная форма матрицы
 имеет вид
имеет вид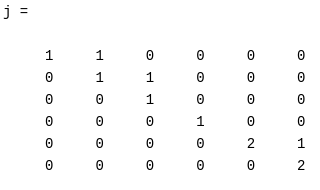
Таким образом, собственному числу 1 соответствуют две клетки размерности 3 и 1, а собственному числу 2 соответствует одна клетка размерности 2.
Построим матрицу
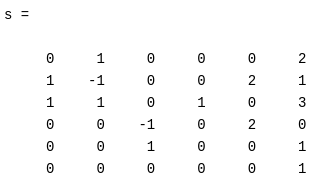
из векторов канонического базиса. Эта матрица является матрицей преобразования подобия
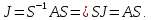 Это формула для проверки правильности ЖНФ и канонического базиса.
Это формула для проверки правильности ЖНФ и канонического базиса.52) Жорданова нормальная форма матрицы линейного оператора в вещественном пространстве
Пусть
 линейное пространство над полем вещественных чисел. Погрузим это пространство в комплексное линейное пространство
линейное пространство над полем вещественных чисел. Погрузим это пространство в комплексное линейное пространство 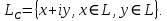 Введем в линейном пространстве
Введем в линейном пространстве 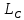 операции сложения и умножения на комплексное число
операции сложения и умножения на комплексное числоНетрудно убедиться в том, что относительно введенных операций сложения и умножения на число
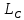 является линейным пространством. В дальнейшем будем полагать, что
является линейным пространством. В дальнейшем будем полагать, что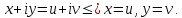
Лемма 1.
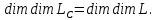
Определение. Линейное пространство
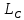 называется комплексным расширением вещественного пространства
называется комплексным расширением вещественного пространства 
Рассмотрим линейный оператор
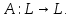 Построим оператор
Построим оператор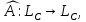 совпадающий с
совпадающий с  на векторах
на векторах  Полагаем по определению
Полагаем по определению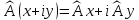
Лемма 2. Оператор
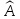 является линейным.
является линейным.Определение. Линейный оператор
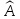 называется расширением линейного оператора
называется расширением линейного оператора  на комплексное пространство
на комплексное пространство 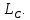
Выберем в
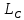 вещественный базис
вещественный базис 
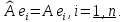
Матрицы линейных операторов
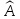 и
и  в указанном базисе совпадают и являются вещественными. Таким образом, характеристический многочлен оператора
в указанном базисе совпадают и являются вещественными. Таким образом, характеристический многочлен оператора 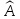 имеет вещественные коэффициенты.
имеет вещественные коэффициенты.Теорема 1. Для любого линейного оператора
 действующего в вещественном линейном пространстве
действующего в вещественном линейном пространстве  существует по крайней мере одно одномерное или двумерное инвариантное подпространство.
существует по крайней мере одно одномерное или двумерное инвариантное подпространство.Замечание. Подпространство
 не содержит ни одного собственного вектора оператора
не содержит ни одного собственного вектора оператора  Матрица индуцированного на
Матрица индуцированного на 
оператора имеет вид
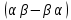 .
.Теорема 2. Пусть
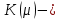 корневое подпространство, соответствующее комплексному собственному числу оператора
корневое подпространство, соответствующее комплексному собственному числу оператора 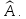
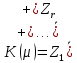 ,
,где
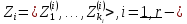 циклические подпространства.
циклические подпространства.Тогда
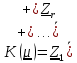 , где
, где 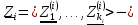 циклические подпространства.
циклические подпространства.Теорема 3. Существует вещественный базис, в котором матрица линейного оператора
 имеет блочно-диагональный вид
имеет блочно-диагональный вид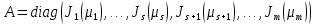 ,
,где
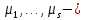 вещественные собственные числа оператора
вещественные собственные числа оператора  соответствующие им клетки Жордана имеют вид
соответствующие им клетки Жордана имеют вид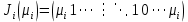 ,
, 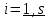 .
.Парам комплексно-сопряженных собственных чисел
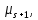
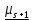 , …,
, …,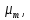
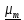 соответствуют обобщенные клетки Жордан
соответствуют обобщенные клетки Жордан