Файл: 1 Определение линейного пространства. Следствия из аксиом. Линейное пространство.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 120
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1) Определение линейного пространства. Следствия из аксиом.
Линейное пространство - множество элементов произвольной природы, для которых выполнены:
-
Имеется правило, по которому любым двум элементам множества ставится ! элемент того же множества, называемый их суммой.
-
Имеется правило, по которому любому элементу из множества и любому вещественному числу ставится в соответствие ! элемент, называемый произведением элемента на число.
-
Относительно введенных операций выполнены следующие аксиомы:
-
x+y=y+x -
(x+y)+z=x+(y+z) -
Существует нулевой элемент -
Существует противоположный элемент для каждого элемента -
1*х=х
-
λ(μx)=(λμ)x -
(λ+μ)x=λx+μx -
λ(x+y)=λx+λy
Элемент линейного пространства - вектор.
Теорема 1. В произвольном линейном пространстве существует единственный нулевой элемент и для каждого элемента существует единственный противоположный элемент.
Теорема 2. В произвольном линейном пространстве:
-
Нулевой элемент = произведение произвольного элемента на 0
-
Противоположный элемент= произведение элемента на -1
Теорема 3. Существует единственный элемент z, удовлетворяющий соотношению y + z = x, называемый разностью элементов х и у (z=x-y)
Свойства линейных пространств:
-
Число*нулевой вектор=нулевой вектор -
Если число*вектор=0, то либо число=0, либо вектор нулевой
-
(-число)*вектор=-(число*вектор)=число*(-вектор) -
Число(вектор1-вектор2)= Число*вектор1- Число*вектор2 -
(Число1-Число2)вектор= Число1*вектор- Число2*вектор
2) Линейная зависимость и независимость
Линейная комбинация векторов е1...еn есть сумма Σai*ei, где ai вещественные
Линейная оболочка - множество всевозможных линейных комбинаций заданной системы векторов.
Свойства линейных оболочек:
-
Линейная оболочка - линейное пространство -
Линейная оболочка содержится в линейном пространстве V.
Если z= Σai*ei ei= Σbij*yj, то z= Σai* bij*yj
Вектора называются линейно зависимыми, если Σai*ei=0 и ai!=0 одновременно
Вектора называются линейно независимыми, если равенство ЛК нулю возможно только в случае, когда все ai=0
Теорема 1. Чтобы вектора были линейно зависимыми необходимо и достаточно, чтобы один из них был линейной комбинацией остальных.
Справедливы следующие утверждения:
-
Если среди элементов имеется нулевой, то система линейно зависима.
-
Если часть векторов линейно зависима, то и вся система линейно зависима.
-
Если вся система линейно независима, то и любая её подсистема линейно независима.
3) Теорема о числе линейных комбинаций. Эквивалентные системы векторов.
Теорема 1. Если число линейных комбинаций больше числа комбинируемых векторов, то комбинации линейно зависимы
Две системы называются эквивалентными, если любой вектор одной системы линейно выражается через вектора другой системы.
Понятие эквивалентности двух систем векторов является отношением эквивалентности, т.е. выполнены симметричность, рефлексивность, транзитивность.
Теорема 2 Чтобы две системы были эквивалентными необходимо и достаточно, чтобы их линейные оболочки совпадали
Теорема 3 Эквивалентные линейно независимые системы состоят из одного и того же числа векторов.
4) Базис и размерность линейного пространства.
Совокупность линейно независимых векторов называется базисом, если любой вектор системы представим в виде линейной комбинации векторов из этой сов-ти.
Теорема 1 Любой вектор может быть разложен по базису единственным образом.
Теорема 2 При сложении двух векторов их координаты складываются, при умножении на число, умножаются на это число.
Линейное пространство называется n-мерным, если в нём существует n линейно независимых векторов, а любая система из n+1 векторов линейно зависима. N=dimV размерность.
Теорема 3. Если пространство размерности n, то любые n линейно независимых вектора образуют базис.
Теорема 4. Если пространство имеет базис, состоящий из n векторов, то размерность пространства n.
Пространство называется конечномерным, если n конечное число.
5) Изоморфизм линейных пространств.
Два пространства называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие так, что: x+y->x’+y’ ax->ax’
Теорема 1. Чтобы два пространства были изоморфными, необходимо и достаточно, чтобы их размерности совпадали.
Следствие. Чтобы система векторов была линейно независима, необходимо и достаточно, чтобы их образы в изоморфном пространстве были линейно независимы. (аналогично для зависимости)
6) Матрица перехода от базиса к базису. Преобразование координат.
f1=t11*e1+t21*e2+...+tn1*en …….
⎨ fn=t1n*e1+t2n*e2+...+tnn*en
t11 t12...t1n
T=⎛ t21 ... ⎞
… ...
⎝ tn1 tn2...tnn ⎠ Матрица перехода от Е к F. Она всегда невырожденная.
Лемма 1.Если Т - матрица перехода от Е-базиса к F-базису, R - матрица перехода от F- базиса к G-базису, то H=T*R - матрица от Е к G.
Лемма 2. Если Т - матрица перехода от Е-базиса к F-базису, то T^-1 матрица перехода от F-базиса к Е-базису.
7) Подпространства линейных пространств.
Подмножество Р является подпространством L, если оно самое является пространством относительно введенных в L операций сложения и умножения на число.
Теорема 1. Для того, чтобы непустое множество Р было подпространством L, необходимо и достаточно, чтобы
-
для любых х и у из Р, их сумма также принадлежала Р -
для любого х, ах также принадлежала Р.
Теорема 2. Размерность подпространства <= размерности пространства. dim P = dim L <=> P=L.
Рангом системы векторов называется максимальное число линейно независимых векторов этой системы.
Теорема 3. Линейная оболочка системы векторов есть минимальное подпространство, содержащее все вектора данной системы, причём его размерность есть ранг системы.
8) Подпространство решений линейной однородной системы.
Рассмотрим систему Ах=0
Теорема 1 Множество решений Р однородной системы линейных уравнений является подпространством Rn размерности n-r, где r=rangA
Вектора ФСР - базис Р
Теорема 2. Если вектора е1...ек образуют базис к-мерного подпространства Р n мерного пространства L, то базис е1..ек можно дополнить векторами е(к+1)...еn до базиса L
Теорема 3. Каждое подпространство Rn определяется линейной однородной системой.
Замечание. Такое определение не однозначно
9) Сумма и пересечение линейных подпространств. Формула Грассмана.
Суммой двух подпространств называются все вектора х=у+z, где y принадлежит одному подпространству, z другому.
Пересечением называется множество векторов, содержащее элементы двух подпространств одновременно.
Теорема 1. Сумма и пересечение являются линейными подпространствами
Теорема 2. Формула Грассмана dim(p+q)+dim(p∩q)=dimp+dimq
10) Построение базиса суммы и пересечения линейных подпространств
Рассмотрим изоморфное L арифметическое пространство Rn координатных столбцов векторов из L. Каждому базисному вектору в соответствие поставим аналогичный столбец из Rn. Введём в рассмотрение матрицу
A=(E1...Em1,F1...Fm2)
dim(P+Q)=rangA
Базис Р может быть дополнен векторами Q до базиса суммы. Достаточно привести матрицу А к трапециевидной форме и выделить линейно независимые столбцы. Соответствующие им вектора образуют базис P+Q.
Пересечение
x=a1e1+...anen=b1f1+...bmfm
a1e1+...anen-(b1f1+...bmfm)=0
запишем последнее в виде системы. Bz=0
rangB=rangA=dim(P+Q)
решение Bz=0
пусть базис суммы образуют e1...en f1...fs
размерность суммы r=n+s
Тогда размерность пространства решений Bz=0
d=n+m-r=m-s
фср Bz=0
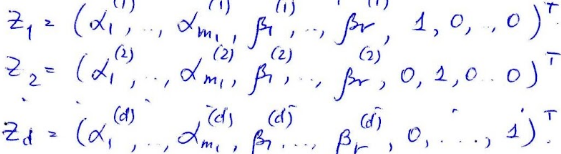
Введём в рассмотрение вектора:
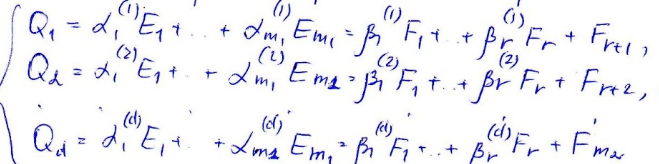
По построению изоморфное перечению подпространство в Rn есть линейная оболочка Q1...Qd
Q1...Qd лнз,т.к. лнз F1...Fm.
Вектора Q1...Qd базис пересечения.
11)Прямая сумма линейных подпространств.
Прямой суммой называется сумма подпространств при условии, что пересечение состоит только из нулевого вектора. P1 ⊕ P2 = {0}
Теорема 1.Чтобы пространство раскладывалось в прямую сумму подпространств, необходимо и достаточно, чтобы любой вектор единственным образом представлялся в виде суммы двух векторов, один из которых принадлежит одному подпр-ву, а другой другому.
Теорема 2. Для того, чтобы пространство раскладывалось в прямую сумму, необходимо и достаточно, чтобы dimL=dimP1+dimP2
Теорема 3 Для того, чтобы пространство раскладывалось в прямую сумму подпространств, необходимо и достаточно, чтобы объединение любых базисов подпространств давало базис пространства.
Следствие: Следующие утверждения эквивалентны для прямой суммы неск. подпр-в
-
Существует единственное представление нулевого вектора в виде суммы слагаемых из подпространств. -
Существует единственное представление вектора пространства в виде суммы слагаемых из подпространств. -
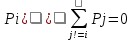
-
Сумма размерностей подпространств= размерности пространств -
Объединение базисов подпространств=базис пространства.
Теорема 4. Существует подпространство P2: P1⊕P2=L. P2 называют прямым дополнением к P1 относительно L.
12) Фактор-пространство.
Будем говорить, что вектора сравнимы по модулю Р, если x-y∊P
x≡y(modP)
Очевидные свойства сравнений:
-
x≡x -
Если x≡y, то у≡х -
транзитивность -
Если x≡y u≡v, то x+u≡y+v -
Если x≡y, то ax≡ay
Класс векторов, сравнимых по модулю P c x будем обозначать
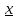
Теорема 1.Два класса сравнимых по модулю P векторов
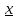 и
и 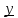 либо не пересекаются, либо совпадают.
либо не пересекаются, либо совпадают.Следствие. Если вектора x и y сравнимы по модулю P, то
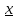 =
=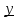
Теорема 2.
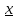 +
+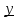 =
=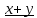 a
a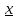 =
=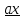
Множество всех классов векторов, сравнимых по модулю P обозначим L/p
Теорема 3 Множество L/p всех классов векторов сравнимых по модулю P образуют линейное пространство, которое называют фактор-пространством.
Теорема 4 dimL/p=dimL-dimP
13) Линейные многообразия
Линейный многообразием линейного пространства L называется совокупность векторов M полученная прибавлением ко всем векторам подпространства Р одного и того же вектора X0
Лемма. Класс векторов
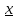 сравнимых с x по модулю P образует линейное многообразие
сравнимых с x по модулю P образует линейное многообразиеТеорема. Чтобы многообразия были равны, необходимо и достаточно, чтобы подпространства были равны и X1-X2 принадлежал пересечению подпространств
Теорема. Для того, чтобы множество было линейным многообразием, необходимо и достаточно чтобы вместе с векторами X1 X2 множеству принадлежали все точки (1 - λ)X1 + λX2 (то есть вся прямая проходящая через указанные точки)
Теорема. Для того, чтобы множество было линейным многообразием, необходимо и достаточно, чтобы множество P всевозможных разностей двух векторов из этого множества было линейным подпространством.
Размерностью линейного многообразия называется размерность направляющего подпространства Р
14) Линейное многообразие решений линейной неоднородной системы.
Рангом линейной неоднородной системы АX = В будем называть r=rangA
Теорема. Всякое линейное многообразие размерности К в пространстве Rn задается линейной /неоднородной системой ранга N - K = r. Обратно, множество решений линейной неоднородной системы ранга r = N - K является линейным многообразием размерности K.
15) Сумма и пересечение линейных многообразий.
Теорема. Сумма и пересечение линейных многообразий являются линейными многообразия.
H0 + H1 = (X0 + X1) + (P0 + P1)
H0 ∩ H1 = X0 + (P0 ∩ P1), где X0 принадлежит H0 ∩ H1
16)Евклидово пространство и его простейшие свойства.
Линейное пространство называется евклидовом пространством если выполнены следующие требования :
-
Имеется правило, посредством которого любым двум элементам x y ставится в соответствии вещественное число, называемое скалярным произведением этих элементов и обозначается (x;y) -
Выполнены аксиомы:
1. (Lx,y)=L(x,y)
2. (x,y1+y2)=(xy1)+(xy2)
3. (x,y)=(у,х)
4.(х,х) >= 0, при этом (x, x) = 0 <=> x = 0
Неравенство Коши-Буняковского.
(x,y)^2<=(x,x)(y,y)
Свойства скалярного произведения:
-
(y1 + y2, x) = (y1, x) + (y2, x) -
(x, Ly) = L(x, y) -
(x, y1 - y2) = (y1 - y2, x) = (x, y1) - (x, y2) -
(x, 0) = 0
Линейное пространство называется нормированным если выполнены следующие требования :
-
Имеется правило посредством которого каждому элементу ставится в соответствии вещественное число называемое нормой указанного элемента и обозначается ॥x॥ -
Выполнены аксиомы:
1.
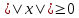 , причем ||x|| = 0 ⇔ x = 0
, причем ||x|| = 0 ⇔ x = 02.

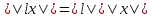
3.
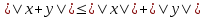
Всякое евклидово пространства является нормированным, если в нём норму элемента определить равенством
॥x॥=
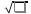
Углом между элементами X и Y назовем угол косинус которого определяется соотношением:
cos =
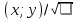
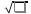
Два произвольных элемента X и Y назовем ортогональными если скалярное произведение X и Y=0
||x + y||^2 = ||x||^2 + ||y||^2, если (x, y) = 0 - аналог т. Пифагора
17) Унитарное пространство и его простейшие свойства.
Линейное пространство называется унитарным если выполнены следующие требования:
-
Имеется правило, посредством которого любым элементам X и Y ставится в соответствие комплексное число (X, Y), называемое их скалярным произв-ем -
Выполнены аксиомы:
1. (Lx,y)=L(x,y)
2. (x1 + x2,y)=(x1, y)+(x2, y)
3. (x,y)=
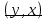
4.(х,х) вещественное неотрицательное число, равное 0 т. и т. т. когда x = 0
Простейшие свойства:
-
(x,Ly)=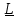 (x,y)
(x,y) -
(x,y1+y2)=(x, y1)+(x, y2)
Теорема. Для любых X и Y, принадлежащих унитарному пространству справедливо неравенство Коши-Буняковского
|(x, y)|^2 <= (x, x)(y, y)
Теорема. Унитарное пространство с нормой ||x||=
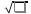 образуют нормированное пространство
образуют нормированное пространство 18) Ортонормированный базис и его существование.
Будем говорить, что ненулевые элементы е1...еk образуют ортогональную систему если
(ei;ej)=0 при i!=j
Теорема.Ортогональная система ненулевых векторов является линейно независимой
Следствие.Число ненулевых векторов в ортогональной системе <= размерности пространства
Система векторов Унитарного пространства называется ортонормированной если
(ei;ej)=
Теорема. Во всяком n-мерном унитарном евклидовом пространстве существует ортонормированный Базис.
e1=f1/||f1||
…
en=gn/||gn|| где gn=fn-(
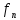
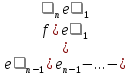
Свойства ортонормированного базиса:
1. (x, y) = Σxi * [сопряженное к yi]
2.
-
Матрица перехода от одного ортонормированного базиса к другому унитарна -
Равенство Парсеваля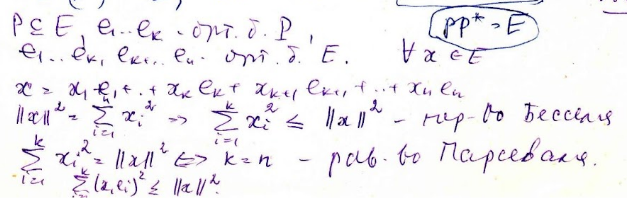
Теорема. для того чтобы векторы e1, …, en образовывали ортонормированный Базис необходимо и достаточно чтобы для любого вектора X
19) Ортогональное дополнение
Вектор y из унитарного пространства U ортогонален подпространству Р, если у ортогонален х для любого х из Р
Теорема 1:Множество ортогональных Р векторов является подпространством L и называется ортогональным дополнением
Теорема 2: Для того, чтобы вектор у принадлежал ортогональному дополнению, необходимо и достаточно, чтобы у был ортогонален всем векторам какого-либо базиса подпространства Р
Теорема 3: унитарное пространство U есть прямая сумма Р и его орт. доп.
Теорема 4: Ортогональное дополнение ортогонального дополнения подпространства Р есть само Р
Теорема 5:
Сумма подпространств называется ортогональной, если слагаемые попарно ортогональны
Лемма: Ортогональная сумма подпространств является прямой суммой
Теорема 6:
Пространство есть ортог. сумма тогда и только тогда, когда (x, y) = (x1, y1) + … +
+(xm, ym) для произвольных x, y из E. Здесь xi, yi принадлежат i-му слагаемому
20) Определитель Грама. Связь с линейной зависимостью
Определитель вида
 называется определителем Грама, составленным для векторов е1… ek∈ Е(U)
называется определителем Грама, составленным для векторов е1… ek∈ Е(U)Теорема: Чтобы система векторов x1...xm была линейно зависимой, необходимо и достаточно, чтобы определитель Грама, составленный из этих векторов, был равен нулю.
Теорема 2: Г(x1...xm) ≥ 0 ∀x1...xm
Замечание: Г(х1...xm) обязательно действительное число, так как соответствующая матрица Грама симметрическая
Замечание 2: Если какой-либо главный минор определителя Грама равен нулю, то равен нулю и сам определитель Грама, так как этот минор будет являться определителем Грама для части векторов
21) Ортогональное проектирование
Всякий вектор x представим ! образом в виде суммы x’ и x’’, где x’ входит в P, x’’ входит в его ортог. дополнение
Вектор x’ называется ортогональной проекцией вектора X на подпространство P, a x’’- ортогональной составляющей x над P
Теорема 3: Г(x1, …, xm) = Г(x1...x(m-1)) * ||hm||^2, где hm - ортогональная составляющая вектора xm на Р =
22) Геометрический смысл определителя Грама. Неравенство Адамара
Пусть x1, …, xm - лнз система векторов
Определим V(x1, …, xm) - трехмерный объем как V(x1, …, x(m - 1)) * ||hm||, где hm - ортогональная составляющая вектора xm на Р =
Теорема: Vm(x1...xm) =

Теорема 2 (неравенство Адамара): Г(x1...xm) ≤Г(x1)⋅Г(x2)⋅...⋅Г(xm)
23) Подпространства в евклидовых пространствах. Углы и расстояния
Расстоянием между векторами x, y будем называть p(x,y) = ||x-y||
Свойства расстояния между векторами:
-
p(x,y) = p(y,x) -
p(x,y) > 0, если x<>y, p(x,y) = 0, если x=y -
p(x,y) <= p(x,z) + p(z,y) - неравенство треугольника
Расстояние от вектора x∊E до подпространства P⊆E: p(x,P) = inf p(x,y) (y∊P)
Теорема 1:
-
p(x,P) = p(x,x1) = ||x2||, где x1 - ортогональная проекция x на P; x2 - ортогональная составляющая -
∀ y ∈ P p(x+y, P) = p(x,P)
Углом между вектором x и подпространством P будем называть α(x,P) = inf α(x,y) (y∈P)
Теорема 2 α(x,P) = α(x, x1), x1 - ортогональная проекция x на P
Теорема 3 Пусть е1... ek - ортонормированный базис подпространства P ⊆ E, αi = α(x,ei). Тогда угол α=α(x, P) удовлетворяет условию
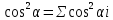 , i =
, i = 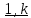 (x - любой единичный вектор
(x - любой единичный векторСледствие 1: Пусть e1...en - ортонормированный базис Е, x - ∀ единичный вектор из Е, α(x,ei) = αi, тогда
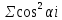 = 1 = ||x||²
= 1 = ||x||²Следствие 2: Углы, которые вектор x образует с произвольным подпространством P и его ортогональным дополнением P┴, в сумме равны
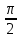
24) Линейные многообразия в евклидовых пространствах
Теорема 1:Для любого вектора х ∈E существует единственное разложение вида x = x1 + x2 где x1∊H, x2∊P┴ (H = x0 + P - линейное многообразие в Е)
Расстоянием от вектора х до линейного многообразия H называется p(x, H) = inf p(x,y) (y∈H)
Теорема 2 p(x, H) = ||x2||, x2 - Ортогональная составляющая вектора х на множестве H
Следствие: p(x,H) = p(x,x1), где x1 - ортогональная проекция вектора x на многообразие H
Теорема 3:p(x,H) = p(x-x0, P)
Линейное многообразие размерности n -1 в n-мерном евклидовом пространстве E будем называть гиперплоскостью
Теорема:
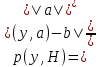 , H задано уравнением (x,a) = b
, H задано уравнением (x,a) = bСледствие: Проекция вектора y на гиперплоскость H имеет вид y1 = y -
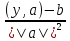 ⋅a
⋅aРасстоянием между линейными многообразиями H1 = x1 + P1 и H2 = x2 + P2 называется p(H1, H2) = inf ||z1 - z2||, z1∈H1, z2∈H2
Теорема: p(H1, H2) = p(x1-x2, P1 + P2)
25) Изоморфизм унитарных пространств
Унитарные пространства будем называть изоморфными, если между векторами этих пространств можно установить взаимно-однозначное соответствие, удовлетворяющее следующим свойствам (x↦x’, y↦y’)
-
x+y ↦x’ + y’ -
λx ↦ λx’ -
(x,y) = (x’, y’)
Теорема: Для того чтобы два унитарных пространства были изоморфны необходимо и достаточно, чтобы были равны размерности этих пространств
26) Линейное отображение. Основные свойства
Правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y из непустого множества Y называется отображение множества X в множество Y (y = φ(x); φ: x↦y; X↦Y), X - область определения отображения φ, y - образ элемента x, x - прообраз элемента у)
Отображение φ: z ↦z’ называется линейным, если ∀x,y∈Z, ∝, β∊P
[φ(∝x + βy) = ∝φ(x) + βφ(y)]
-
φ(x+y) = φ(x) + φ(y) - аддитивность -
φ(∝x) = ∝φ(x) - однородность
Примеры:
-
φ(x) = x - тождественное отображение Z в Z -
φ(x) = 0’ - нулевое отображение -
проектирование вектора на плоскость -
дифференцирование функций -
интегрирование функций
Свойства линейных отображений:
-
φ(0) = 0’, 0 ∈L, 0’ ∈L’ -
φ(-x) = -x’ -
φ(α1x1 + … + αnxn) =α1φ(x1) + … +αn φ(xn) -
コz =и φ(z) = z’, то есть ∀y∈Z’ ∃ прообраз x∊Z, тогда z’ = <φ(a1),...,φ(an)>
Если x1,...,xn линейно зависимы, то φ(x1), … φ(xn) линейно зависимы
Отображения φ и ψ считаем равными, если ∀x∊L φ(x) = ψ(x)
Лемма: コ Z = Lin
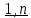
-
Если φ(x1)...φ(xn) линейно независимы, то x1...xn независимы
Теорема: Пусть e1...en - базис линейного пространства Z. Выберем в Z’ произвольные векторы a1’...an’. Тогда Ǝ! линейное отображение Z на Z’, переводящее векторы e1...en в векторы a1’...an’ соответственно
27) Пространство линейных отображений
-
⊐ L =L < > и L -> L’, т.е. для любого y ∈ L’ ∃ прообраз x ∈ L => L’ = <
> и L -> L’, т.е. для любого y ∈ L’ ∃ прообраз x ∈ L => L’ = <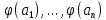 >
> -
Если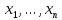 линейно зависимы, то
линейно зависимы, то 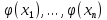 линейно зависимы
линейно зависимы -
Если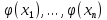 линейно независимы, то
линейно независимы, то 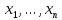 линейно независимы
линейно независимы
Рассмотрим линейные пространства L и L’ над одним числовым полем и множество всех линейных отображений L на L’. На этом множестве введем операции сложения и умножения на число.
Линейное отображение φ называется суммой линейных отображений φ1 и φ2, если выполнено равенство φ(x) = φ1(x) + φ2(x)
Линейное отображение φ называется произведением линейного отображения ψ на число λ из поля P, если выполняется равенство φ(x) = λψ(x)
Теорема: Множество линейных отображений из z в z’ относительно введенных операций сложения и умножения на число образуют линейное пространство
пространство линейных отображений Hom(z z’)
Теорема: dim Hom(z z’)=dim z*dimz’
Рассмотрим три линейных пространства L, L’, L’’ над одним полем P.
 : L↦L’; ψ: L’↦L’’
: L↦L’; ψ: L’↦L’’Отображение Х называется произведением линейных отображений
 и ψ, если выполняется равенство:
и ψ, если выполняется равенство:X(x) = ψ(
 (x)); ∀x ∈ L; X: L↦L’’
(x)); ∀x ∈ L; X: L↦L’’ Утверждение: Произведение линейных отображений - линейное отображение
Теорема: Множество линейных отображений L на L’ относительно операций сложения и умножения образует ассоциативное кольцо (т.е. сложение коммутативно, ассоциативно, есть нейтральный и противоположный элемент относительно сложения, умножение ассоциативно, есть дистрибутивность)
Пусть
 принадлежит множеству линейных отображений L на L’.
принадлежит множеству линейных отображений L на L’. 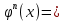
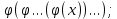
Утверждение:
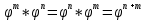 - доказывается по индукции
- доказывается по индукцииМногочленом от линейного отображения
 будем называть F(
будем называть F( ) =
) = 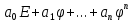
Теорема: Два многочлена от одного линейного отображения перестановочны между собой: F(
 )G(
)G( ) = G(
) = G( )F(
)F( )
)28) Ядро и образ линейного отображения
Ядром(ker) линейного отображения
 будем называть множество векторов x ∈ L :
будем называть множество векторов x ∈ L : (x) = 0’
(x) = 0’Образом (областью значений (Jm)) линейного отображения
 будем называть совокупность образов всех векторов x ∈ L
будем называть совокупность образов всех векторов x ∈ L Теорема: Ядро и образ линейного отображения являются линейными подпространствами соответственно L и L’.
Размерность ядра
 называется дефектом линейного отображения.
называется дефектом линейного отображения.Размерность образа
 называется рангом линейного отображения.
называется рангом линейного отображения.Теорема: Сумма дефекта и ранга линейного отображения есть размерность L.
Теорема: Если V подпространство L, V’ подпространство L’ такие, что dimV+dimV’=dimL. Тогда существует такое линейное отображение
 из L в L’, что V=ker
из L в L’, что V=ker , V’=Jm
, V’=Jm
29) Невырожденное линейное отображения.
Линейное отображение называется невырожденным, если его ядро состоит только из нулевого вектора.
Следствие:
 - невырожденное → Ранг
- невырожденное → Ранг  равен размерности L
равен размерности LТеорема: Чтобы линейное отображение
 было невырожденным, необходимо и достаточно, чтобы оно было взаимооднозначным (мономорфизмом), то есть различным векторам соответствуют различные образы.
было невырожденным, необходимо и достаточно, чтобы оно было взаимооднозначным (мономорфизмом), то есть различным векторам соответствуют различные образы. Отображение
 , переводящее L’ в L, называется обратным линейным отображением
, переводящее L’ в L, называется обратным линейным отображением  если
если 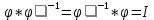 где I тождественное отображение.
где I тождественное отображение.При этом такое отображение может быть определено не на всем Z’
Теорема:
 -невырождено <->
-невырождено <->  обратимо.
обратимо. 
Теорема: Произведение любого конечного числа невырожденных отображений есть также невырожденное отображение.
Теорема: Множество невырожденных отображений
 является группой по умножению (то есть умножение ассоциативно, имеется нейтральный элемент относительно умножения, элементы обратимы относительно умножения).
является группой по умножению (то есть умножение ассоциативно, имеется нейтральный элемент относительно умножения, элементы обратимы относительно умножения).30) Матрица линейного отображения
Рассмотрим линейное отображение
 : L→ L’
: L→ L’Пусть
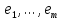 - базис L
- базис L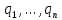 - базис L’
- базис L’Применим отображение
 к базисным векторам:
к базисным векторам: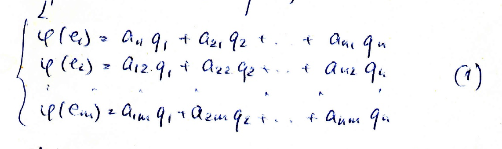 (1)
(1)Коэффициенты
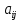 определяют матрицу
определяют матрицу 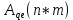
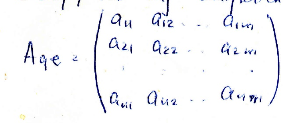 (2)
(2), которая называется матрицей линейного отображения
 в выбранных базисах.
в выбранных базисах.Столбцами матрицы линейного отображения являются координаты образов базисных векторов L.
Установим связь между ∀x ∈ L и его образом y =
 (x)∈ L’ (3)
(x)∈ L’ (3)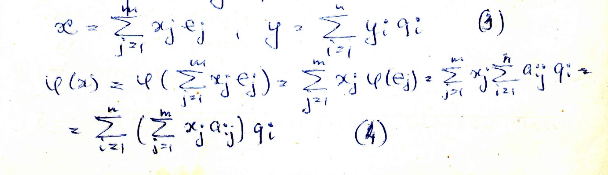 (4)
(4)Отсюда совокупность равенств
или в матричной форме
При попытке вычислить неизвестные
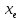 по известным
по известным 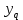 получаем неоднородную систему линейных уравнений.
получаем неоднородную систему линейных уравнений.Из (6) следует, что ранг линейного отображения совпадает с рангом матрицы линейного отображения, а его дефект - с числом фундаментальных решений соответствующей однородной системы.
Выберем в пространстве L другой базис
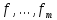 , а в L’ соответственно
, а в L’ соответственно 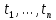
Аналогично (6) запишем
где
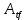 - матрица линейного отображения
- матрица линейного отображения  в паре базисов
в паре базисов 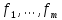 и
и 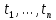
Установим связь матриц
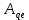 и
и 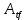
Пусть T - матрица перехода от базиса
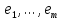 к базису
к базису 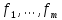 , а Q - матрица перехода от базиса
, а Q - матрица перехода от базиса 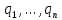 к базису
к базису 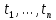 : (8)
: (8)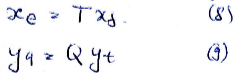 (9)
(9)Подставляем (8) и (9) в (6):
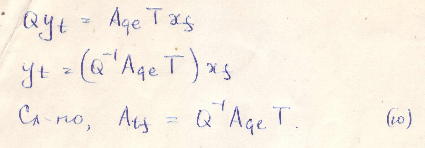 (10)
(10)(10) связывает матрицы одного линейного отображения в разных парах базисов
1 2 3 4 5 6
31) Относительный базис линейного пространства. Канонический вид матрицы линейного отображения.
Рассмотрим линейное пространство
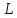 и его подпространство
и его подпространство 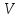 .
.Вектора
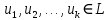 будем называть линейно независимыми относительно подпространства
будем называть линейно независимыми относительно подпространства 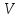 , если
, если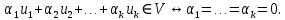
Теорема: Пусть
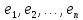 – базис подпространства
– базис подпространства 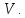 Вектора
Вектора 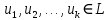 будут линейно независимыми относительно подпространства
будут линейно независимыми относительно подпространства 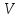 , тогда и только тогда, когда совокупность векторов
, тогда и только тогда, когда совокупность векторов 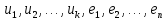 линейно независима в обычном смысле.
линейно независима в обычном смысле.Будем говорить, что вектора
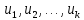 образуют базис пространства
образуют базис пространства 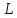 относительно подпространства
относительно подпространства 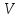 , если
, если-
вектора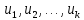 линейно независимы относительно
линейно независимы относительно 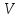
-
для любого вектора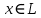 имеет место представление
имеет место представление
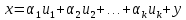 , где
, где 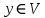 .
.Теорема: Для того, чтобы вектора
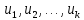 были базисом пространства
были базисом пространства 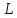 относительно подпространства
относительно подпространства 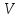 , необходимо и достаточно, чтобы вектора
, необходимо и достаточно, чтобы вектора 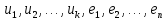
были базисом
 , где
, где  базис
базис 
Канонический вид матрицы линейного отображения.
Известно, что матрица линейного отображения зависит от выбора пары базисов. Найдем наиболее простой вид этой матрицы и соответствующую ему пару базисов.
Рассмотрим линейное отображение
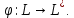 Выберем в
Выберем в  относительный базис
относительный базис 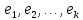 по отношению к ядру
по отношению к ядру 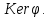 Пусть вектора
Пусть вектора 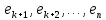 образуют базис ядра. Тогда
образуют базис ядра. Тогда 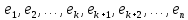 – базис
– базис  в обычном смысле. Покажем, что вектора
в обычном смысле. Покажем, что вектора 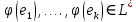 образуют базис образа
образуют базис образа 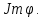 Для любого
Для любого 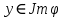 существует
существует  такой, что
такой, что 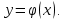
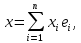
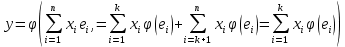 .
.Следовательно,
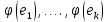 – система образующих для
– система образующих для 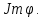
Покажем, что эти вектора линейно независимы.
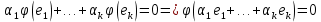
Следовательно,
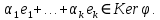 По определению линейной независимости относительно подпространства
По определению линейной независимости относительно подпространства 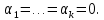 Таким образом,
Таким образом,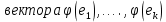 линейно независимы и образуют базис
линейно независимы и образуют базис 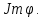 Дополним эти вектора до базиса пространства
Дополним эти вектора до базиса пространства