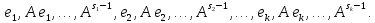Файл: 1 Определение линейного пространства. Следствия из аксиом. Линейное пространство.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 121
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
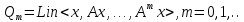
Степень относительного минимального многочлена совпадает с минимальным
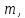 для которого
для которого 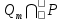 содержит ненулевые векторы.
содержит ненулевые векторы.Пусть
 матрица линейного оператора
матрица линейного оператора  в базисе
в базисе  . Выберем базис
. Выберем базис 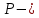
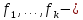 базис
базис 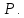 В выбранном базисе найдем координатные столбцы соответствующих векторов.
В выбранном базисе найдем координатные столбцы соответствующих векторов.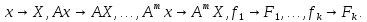
Пусть
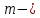 степень относительного минимального многочлена. Составим матрицу
степень относительного минимального многочлена. Составим матрицу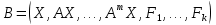
Фундаментальная система решений
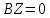 состоит из одного вектора
состоит из одного вектора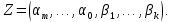
Выбираем единственную произвольную постоянную таким образом, чтобы
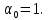 Искомый относительный минимальный многочлен вектора
Искомый относительный минимальный многочлен вектора  :
: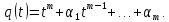
Опр. Ненулевой многочлен P
 будем называть относительным аннулирующим многочленом пространства
будем называть относительным аннулирующим многочленом пространства  относительно подпространства
относительно подпространства  если
если 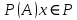 для любого вектора
для любого вектора 
Опр. Ненулевой приведенный многочлен Q
 называется минимальным аннулирующим многочленом пространства
называется минимальным аннулирующим многочленом пространства 
относительно подпространства
 если
если-
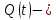 относительный аннулирующий многочлен
относительный аннулирующий многочлен -
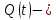 относительный аннулирующий многочлен минимальной степени.
относительный аннулирующий многочлен минимальной степени.
Свойства
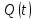 аналогичны свойствам
аналогичны свойствам 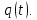
Относительный минимальный многочлен пространства может быть построен как НОК относительных минимальных многочленов базисных векторов.
38) Первая теорема о расщеплении
Теорема 1: (первая теорема о расщеплении)
Если минимальный многочлен
 линейного пространства
линейного пространства  представим в виде произведения двух взаимно простых многочленов
представим в виде произведения двух взаимно простых многочленов 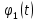 и
и 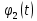 , то пространство
, то пространство  расщепляется в прямую сумму двух инвариантных подпространств
расщепляется в прямую сумму двух инвариантных подпространств 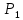 и
и 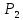 так, что минимальными многочленами данных подпространств являются
так, что минимальными многочленами данных подпространств являются 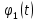 и
и 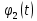 соответственно.
соответственно.(Здесь
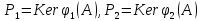 )
)Следствие: Результат теоремы 1 справедлив для произведения конечного числа взаимно простых многочленов.
Теорема 2: Если минимальные многочлены векторов
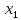 и
и 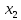 из
из  взаимно просты, то минимальный многочлен их суммы равен произведению минимальных многочленов слагаемых.
взаимно просты, то минимальный многочлен их суммы равен произведению минимальных многочленов слагаемых.Следствие: Результат теоремы 2 справедлив для относительного минимального многочлена вектора.
39) Теорема о существовании вектора, минимальный многочлен которого совпадает с минимальным многочленом пространства.
Теорема 3: В пространстве
 всегда существует вектор, минимальный многочлен которого совпадает с минимальным многочленом всего пространства.
всегда существует вектор, минимальный многочлен которого совпадает с минимальным многочленом всего пространства.40) Циклические инвариантные подпространства
Пусть
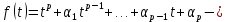 минимальный многочлен вектора
минимальный многочлен вектора 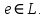 Векторы
Векторы 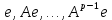 линейно независимы, причем
линейно независимы, причем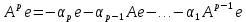
Опр. Подпространство
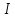 с базисом
с базисом 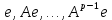 называется циклическим подпространством, порожденным вектором
называется циклическим подпространством, порожденным вектором 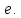
Теорема: Циклическое подпространство
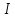 инвариантно относительно линейного оператора
инвариантно относительно линейного оператора 
Теорема: Минимальный многочлен порождающего вектора
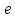 будет одновременно минимальным многочленом всего подпространства
будет одновременно минимальным многочленом всего подпространства 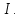
41) Вторая теорема о расщеплении
Теорема: (Вторая теорема о расщеплении)
Пространство
 всегда можно расщепить на циклические относительно данного линейного оператора
всегда можно расщепить на циклические относительно данного линейного оператора  подпространства
подпространства 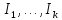 с минимальными многочленами
с минимальными многочленами 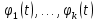
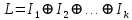
так, чтобы многочлен
 совпадал с минимальным многочленом
совпадал с минимальным многочленом  всего пространства
всего пространства  и каждый многочлен
и каждый многочлен 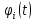
был бы делителем предыдущего многочлена
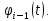
42) Критерии цикличности. Нерасщепимость
Теорема: Для того, чтобы пространство L было циклическим, необходимо и достаточно, чтобы его размерность совпадала со степенью его минимального многочлена
Теорема: Циклическое пространство расщепляется только на такие инвариантные подпространства, которые
-
сами являются циклическими -
имеют взаимно простые минимальные многочлены.
Теорема: Если пространство
 расщепляется на инвариантные подпространства, которые
расщепляется на инвариантные подпространства, которые-
являются циклическими -
имеют взаимно простые минимальные многочлены, то само пространство является циклическим.
Теорема: Пространство не расщепляется на инвариантные подпространства тогда и только тогда, когда
-
оно циклическое -
его минимальный многочлен есть степень неприводимого над данным полем многочлена
43) Третья теорема о расщеплении. Первая и вторая ЕНФ матрицы линейного оператора.
Теорема: (третья теорема о расщеплении)
Пространство всегда можно расщепить на циклические инвариантные подпространства
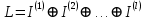
так, чтобы минимальный многочлен каждого из этих циклических подпространств был степенью неприводимого многочлена.
Структура матрицы лин. оп. в случае, если пр-во допускает расщепление на циклические подпр-ва. Эта матрица имеет блочно-диагональный вид.
Расщепим
 по второй теореме о расщеплении
по второй теореме о расщеплении
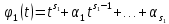
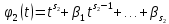
…………………………………..
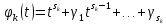 .
.Обозначим через
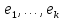 порождающие векторы в подпространствах
порождающие векторы в подпространствах  и составим базис пространства
и составим базис пространства  объединяя базисы подпространств, в прямую сумму которых оно расщепляется
объединяя базисы подпространств, в прямую сумму которых оно расщепляется