Файл: 1 Определение линейного пространства. Следствия из аксиом. Линейное пространство.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 125
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
векторами 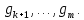
Теперь построим матрицу линейного отображения в паре базисов
в паре базисов
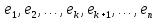 и
и 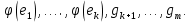 Эта матрица
Эта матрица 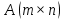 имеет вид
имеет вид
A = (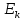 O
O
O O)
Здесь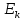 – единичная матрица порядка
– единичная матрица порядка 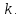 Это канонический вид матрицы линейного отображения.
Это канонический вид матрицы линейного отображения.
32) Линейные операторы. Основные свойства.
Линейное отображение пространства в себя называется линейным оператором
в себя называется линейным оператором 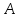 :
: 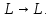
Линейный оператор также характеризуется ядром и образом с той лишь разницей, что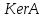 и
и 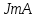 являются подпространствами одного линейного пространства
являются подпространствами одного линейного пространства  .Пусть
.Пусть 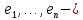 базис
базис  Поставим в соответствие в данном базисе образам базисных векторов координатные столбцы
Поставим в соответствие в данном базисе образам базисных векторов координатные столбцы 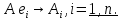
Матрица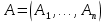 размерности
размерности 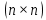 называется матрицей линейного оператора
называется матрицей линейного оператора 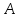 в базисе
в базисе 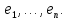
Нетрудно установить взаимно-однозначное соответствие между линейными операторами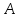 :
: 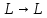
и квадратными матрицами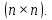
Теорема: Если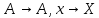 в базисе
в базисе 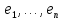 , то
, то 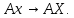
Если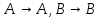 в базисе
в базисе 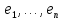 , то
, то 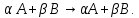
Если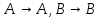 в базисе
в базисе 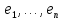 , то
, то 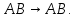
Теорема: Ранг линейного оператора равен рангу матрицы этого оператора
равен рангу матрицы этого оператора  .
.
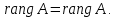
Теорема: Пусть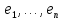 и
и 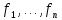 - два различных базиса
- два различных базиса 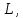
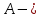 матрица линейного оператора
матрица линейного оператора  в базисе
в базисе  Тогда матрица этого оператора в базисе
Тогда матрица этого оператора в базисе 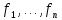 имеет вид
имеет вид 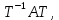 где
где 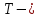 матрица перехода от базиса
матрица перехода от базиса
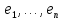 к базису
к базису 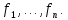
Замечание: Ранг матрицы линейного оператора не зависит от выбора базиса, поскольку матрицы в различных базисах подобны.
Для линейного оператора :
:  справедливо
справедливо
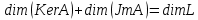 . (*)
. (*)
Пример: Рассмотрим оператор проектирования произвольного вектора из
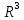 на координатную плоскость
на координатную плоскость 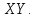 Покажем, что этот оператор является линейным.
Покажем, что этот оператор является линейным.
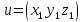 ,
, 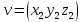
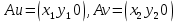
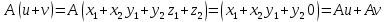
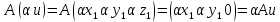
Построим матрицу оператора проектирования в стандартном координатном базисе.
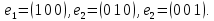
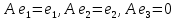
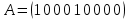
Ядро данного оператора совпадает с осью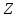 , а образ – с плоскостью
, а образ – с плоскостью 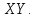
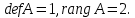
Лемма: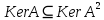 ,
, 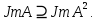
Теорема: Для того, чтобы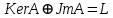 , необходимо и достаточно,
, необходимо и достаточно, 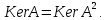
Пример: Оператор дифференцирования в пространстве многочленов степени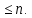
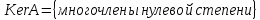
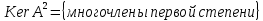
Очевидно,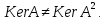
Пусть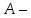 невырожденный линейный оператор. Отметим ряд его очевидных свойств.
невырожденный линейный оператор. Отметим ряд его очевидных свойств.
33) Собственные числа и собственные векторы и пространства.
Пусть A - линейный оператор, действующий из в
в 
 матрица этого оператора в базисе
матрица этого оператора в базисе 
Многочлен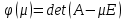 называется характеристическим многочленом оператора
называется характеристическим многочленом оператора 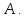
Матрицы линейного оператора в различных базисах подобны, следовательно, характеристический многочлен оператора не зависит от выбора базиса.
Число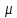 называется собственным числом линейного оператора
называется собственным числом линейного оператора  , если существует ненулевой вектор
, если существует ненулевой вектор 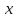 такой, что
такой, что
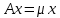 , (1)
, (1)
При этом вектор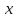 называется собственным вектором оператора
называется собственным вектором оператора  , соответствующим собственному числу
, соответствующим собственному числу 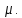
Теорема: Для того, чтобы число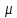 было собственным числом оператора
было собственным числом оператора  , необходимо и достаточно, чтобы это число было корнем характеристического многочлена
, необходимо и достаточно, чтобы это число было корнем характеристического многочлена 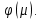
Следствие: Если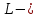 пространство над полем комплексных чисел, то линейный оператор
пространство над полем комплексных чисел, то линейный оператор  имеет по крайней мере одно собственное число.
имеет по крайней мере одно собственное число.
Теорема: Собственные векторы линейного оператора , соответствующие различным собственным числам
, соответствующие различным собственным числам
, линейно независимы.
Следствие: Максимальное число линейно независимых собственных векторов не превосходит размерности пространства
Теорема: Все собственные векторы, принадлежащие собственному числу , вместе с нулевым вектором образуют линейное подпространство.
, вместе с нулевым вектором образуют линейное подпространство.
34) Оператор простой структуры
Алгебраическая кратность собственного числа - кратность собственного числа как корня характеристического многочлена.
Геометрическая кратность собственного числа - максимальное число линейно независимых собственных векторов, соответствующих этому собственному числу.
Обозначим через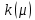 алгебраическую кратность собственного числа
алгебраическую кратность собственного числа  , а через
, а через 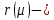 геометрическую кратность этого собственного числа.
геометрическую кратность этого собственного числа.
Теорема: Для любого собственного числа линейного оператора
линейного оператора 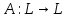
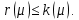
Линейный оператор называется оператором простой структуры, если существует базис пространства
называется оператором простой структуры, если существует базис пространства  , в котором матрица этого оператора диагональна.
, в котором матрица этого оператора диагональна.
Теорема: Для того, чтобы линейный оператор был оператором простой структуры, необходимо и достаточно, чтобы существовал базис, состоящий из собственных векторов этого оператора.
был оператором простой структуры, необходимо и достаточно, чтобы существовал базис, состоящий из собственных векторов этого оператора.
Следствие: Если оператор A имеет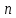 различных собственных чисел, то он является оператором простой структуры. (Этот факт следует из линейной независимости собственных векторов, соответствующих различным собственным числам.)
различных собственных чисел, то он является оператором простой структуры. (Этот факт следует из линейной независимости собственных векторов, соответствующих различным собственным числам.)
Теорема: Для того, чтобы линейный оператор
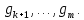
Теперь построим матрицу линейного отображения
 в паре базисов
в паре базисов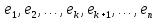 и
и 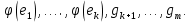 Эта матрица
Эта матрица 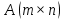 имеет вид
имеет видA = (
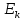 O
OO O)
Здесь
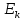 – единичная матрица порядка
– единичная матрица порядка 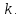 Это канонический вид матрицы линейного отображения.
Это канонический вид матрицы линейного отображения.32) Линейные операторы. Основные свойства.
Линейное отображение пространства
 в себя называется линейным оператором
в себя называется линейным оператором 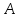 :
: 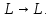
Линейный оператор также характеризуется ядром и образом с той лишь разницей, что
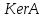 и
и 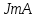 являются подпространствами одного линейного пространства
являются подпространствами одного линейного пространства  .Пусть
.Пусть 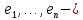 базис
базис  Поставим в соответствие в данном базисе образам базисных векторов координатные столбцы
Поставим в соответствие в данном базисе образам базисных векторов координатные столбцы 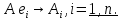
Матрица
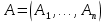 размерности
размерности 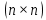 называется матрицей линейного оператора
называется матрицей линейного оператора 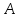 в базисе
в базисе 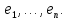
Нетрудно установить взаимно-однозначное соответствие между линейными операторами
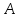 :
: 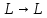
и квадратными матрицами
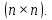
Теорема: Если
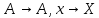 в базисе
в базисе 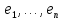 , то
, то 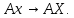
Если
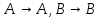 в базисе
в базисе 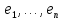 , то
, то 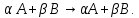
Если
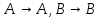 в базисе
в базисе 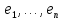 , то
, то 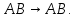
Теорема: Ранг линейного оператора
 равен рангу матрицы этого оператора
равен рангу матрицы этого оператора  .
.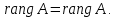
Теорема: Пусть
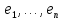 и
и 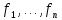 - два различных базиса
- два различных базиса 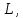
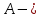 матрица линейного оператора
матрица линейного оператора  в базисе
в базисе  Тогда матрица этого оператора в базисе
Тогда матрица этого оператора в базисе 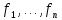 имеет вид
имеет вид 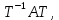 где
где 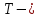 матрица перехода от базиса
матрица перехода от базиса 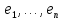 к базису
к базису 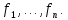
Замечание: Ранг матрицы линейного оператора не зависит от выбора базиса, поскольку матрицы в различных базисах подобны.
Для линейного оператора
 :
:  справедливо
справедливо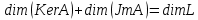 . (*)
. (*)Пример: Рассмотрим оператор проектирования произвольного вектора из
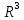 на координатную плоскость
на координатную плоскость 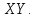 Покажем, что этот оператор является линейным.
Покажем, что этот оператор является линейным.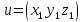 ,
, 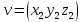
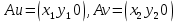
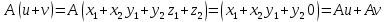
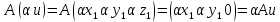
Построим матрицу оператора проектирования в стандартном координатном базисе.
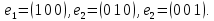
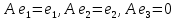
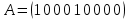
Ядро данного оператора совпадает с осью
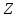 , а образ – с плоскостью
, а образ – с плоскостью 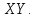
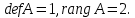
Лемма:
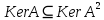 ,
, 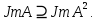
Теорема: Для того, чтобы
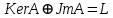 , необходимо и достаточно,
, необходимо и достаточно, 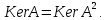
Пример: Оператор дифференцирования в пространстве многочленов степени
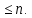
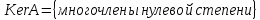
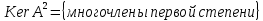
Очевидно,
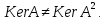
Пусть
 невырожденный линейный оператор. Отметим ряд его очевидных свойств.
невырожденный линейный оператор. Отметим ряд его очевидных свойств.-
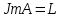
-
Матрица невырождена в любом базисе
невырождена в любом базисе 
-
 переводит любую линейно независимую систему векторов в линейно независимую систему векторов
переводит любую линейно независимую систему векторов в линейно независимую систему векторов -
A^-1 есть матрица обратного оператора в том же базисе, в котором A - матрица самого оператора
33) Собственные числа и собственные векторы и пространства.
Пусть A - линейный оператор, действующий из
 в
в 
 матрица этого оператора в базисе
матрица этого оператора в базисе 
Многочлен
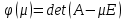 называется характеристическим многочленом оператора
называется характеристическим многочленом оператора 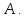
Матрицы линейного оператора в различных базисах подобны, следовательно, характеристический многочлен оператора не зависит от выбора базиса.
Число
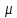 называется собственным числом линейного оператора
называется собственным числом линейного оператора  , если существует ненулевой вектор
, если существует ненулевой вектор 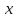 такой, что
такой, что 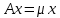 , (1)
, (1)При этом вектор
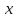 называется собственным вектором оператора
называется собственным вектором оператора  , соответствующим собственному числу
, соответствующим собственному числу 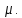
Теорема: Для того, чтобы число
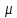 было собственным числом оператора
было собственным числом оператора  , необходимо и достаточно, чтобы это число было корнем характеристического многочлена
, необходимо и достаточно, чтобы это число было корнем характеристического многочлена 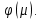
Следствие: Если
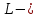 пространство над полем комплексных чисел, то линейный оператор
пространство над полем комплексных чисел, то линейный оператор  имеет по крайней мере одно собственное число.
имеет по крайней мере одно собственное число.Теорема: Собственные векторы линейного оператора
 , соответствующие различным собственным числам
, соответствующие различным собственным числам
, линейно независимы.
Следствие: Максимальное число линейно независимых собственных векторов не превосходит размерности пространства

Теорема: Все собственные векторы, принадлежащие собственному числу
 , вместе с нулевым вектором образуют линейное подпространство.
, вместе с нулевым вектором образуют линейное подпространство.34) Оператор простой структуры
Алгебраическая кратность собственного числа - кратность собственного числа как корня характеристического многочлена.
Геометрическая кратность собственного числа - максимальное число линейно независимых собственных векторов, соответствующих этому собственному числу.
Обозначим через
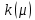 алгебраическую кратность собственного числа
алгебраическую кратность собственного числа  , а через
, а через 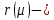 геометрическую кратность этого собственного числа.
геометрическую кратность этого собственного числа.Теорема: Для любого собственного числа
 линейного оператора
линейного оператора 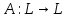
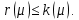
Линейный оператор
 называется оператором простой структуры, если существует базис пространства
называется оператором простой структуры, если существует базис пространства  , в котором матрица этого оператора диагональна.
, в котором матрица этого оператора диагональна.Теорема: Для того, чтобы линейный оператор
 был оператором простой структуры, необходимо и достаточно, чтобы существовал базис, состоящий из собственных векторов этого оператора.
был оператором простой структуры, необходимо и достаточно, чтобы существовал базис, состоящий из собственных векторов этого оператора.Следствие: Если оператор A имеет
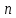 различных собственных чисел, то он является оператором простой структуры. (Этот факт следует из линейной независимости собственных векторов, соответствующих различным собственным числам.)
различных собственных чисел, то он является оператором простой структуры. (Этот факт следует из линейной независимости собственных векторов, соответствующих различным собственным числам.)Теорема: Для того, чтобы линейный оператор