Матрица линейного оператора в этом базисе имеет вид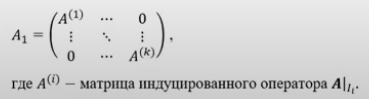



Про матрицу 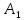будем говорить, что она имеет первую естественную нормальную форму (ЕНФ) (первую нормальную форму Фробениуса).

Если проделать аналогичную процедуру на основе третьей теоремы о расщеплении, то получим блочно-диагональную матрицу 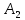, которая имеет вторую ЕНФ (вторую нормальную форму Фробениуса).

44)Корневые подпространства

Пусть линейный оператор, действующий в комплексном линейном пространстве размерности 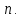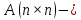матрица этого оператора в некотором базисе. Обозначим через характеристический многочлен данного оператора.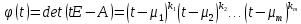

(1)

Здесь 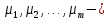различные собственные числа оператора, а 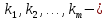их алгебраические кратности,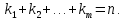

Подставим вместо переменной 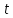в (1) оператор .

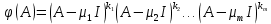, (2)

здесь 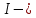тождественный оператор.

Опр. Совокупность всех векторов удовлетворяющих условию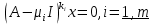

(3)

будем называть корневым подпространством, соответствующим собственному числу

---

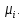
Вектора из корневого подпространства называются корневыми векторами.

Замечание. Собственные вектора, соответствующие собственному числу

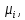
являются корневыми векторами.

Теорема 1.

Индуцированный на корневом подпространстве 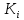линейный оператор имеет единственное собственное число

Теорема 2.

Комплексное линейное пространство представляет собой прямую сумму инвариантных корневых подпространств линейного оператора 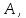соответствующих его различным собственным числам.

Следствие.

Размерность корневого подпространства совпадает с алгебраической кратностью соответствующего собственного числа.

45) Высота корневого вектора

Опр. Высотой корневого вектора 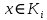называется наименьшее натуральное 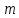такое, что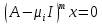



Теорема.

Корневые векторы из 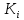попарно различных высот линейно независимы.

Замечание.

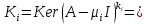корневое подпространство является инвариантным.

Пусть 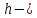максимально возможная высота корневых векторов в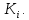

Теорема.

Для любого 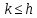множество корневых векторов 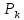, высота которых не превосходит 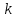, образует линейное подпространство.

Замечание.

Если имеет высоту то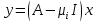

---

имеет высоту

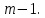
46) Разложение пространства в прямую сумму корневых подпространств

Теорема.

Комплексное линейное пространство представляет собой прямую сумму инвариантных корневых подпространств линейного оператора соответствующих его различным собственным числам.

Следствие.

Размерность корневого подпространства совпадает с алгебраической кратностью соответствующего собственного числа.

47) Характеристический и минимальный многочлен оператора

Рассмотрим линейный оператор , действующий в линейном пространстве . Пусть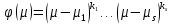



характеристический многочлен оператора

Теорема 1.

Минимальный многочлен пространства имеет вид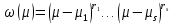

,

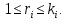
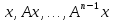Теорема 2. Для того, чтобы характеристический многочлен оператора и минимальный многочлен пространства совпадали, необходимо и достаточно, чтобы существовал вектор такой, что векторы линейно независимы,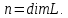

Теорема 3. Для каждого корневого подпространства имеем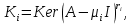



где 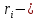кратность собственного числа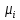

---

как корня минимального многочлена.

Следствие. Максимальная высота корневого вектора в равна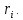

Теорема 4.Для того, чтобы оператор был оператором простой структуры, необходимо и достаточно, чтобы минимальный многочлен пространства имел только простые корни.

48) Структура инвариантных подпространств

Опр. Подпространство линейного пространства называется инвариантным относительно линейного оператора , если для любого вектора его образ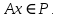

Для любого линейного оператора существует по крайней мере два инвариантных подпространства – нулевое подпространство и все пространство Они называются тривиальными инвариантными подпространствами.

Теорема 1. Инвариантными подпространствами линейного оператора являются его ядро, образ и произвольное собственное подпространство.

Теорема 2. Сумма и пересечение инвариантных подпространств являются инвариантными подпространствами.

Инвариантные подпространства и 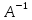совпадают.

Пусть подпространство размерности , инвариантное относительно линейного оператора Существует такое подпространств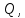о что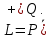

---

Пусть базис пространства где базис а базис

A

A

Матрица оператора в выбранном базисе ступенчатая.



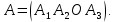
Если подпространство 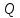тоже инвариантно, то матрица оператора блочно- диагональная.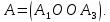



Опр. Оператор A, определенный только для векторов некоторого инвариантного подпространства, будем называть индуцированным на этом подпространстве.

индуцированный оператор на подпространстве A порождающий оператор.

Пусть матрица индуцированного оператора в базисе

матрица индуцированного оператора в базисе

Теорема 3. Характеристический многочлен порождающего оператора равен произведению характеристических многочленов соответствующих индуцированных операторов.

49) Разложение корневого подпространства в прямую сумму циклических подпространств

---

Смотрите также файлы

• Инструмент оснастка Инструмент оснастка.docx

• 1. 1 Школа и семья как субъекты образовательного процесса.doc

• Образовательное учреждение высшего образования мордовский государственный педагогический университет имени м. Е. Евсевьева.docx

• Отчет по дисциплине Экономика финансы и организации Практикум Тема Доходы и финансовые результаты организации обучающийся группы дбэ101бд Абраам Абрамян Хоренович.docx

• Практическая работа 5 Быстрота Особенности возрастного периода 1215 лет.docx