ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 98
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В связи с тем, что для каждого участка траектории требуется определить Nтраекторий присоединенных переменных, то в этом случае удобно воспользоваться нормированным временем t
Каждая система полиномов должна удовлетворять определенным граничным условиями:
-
Начальное положение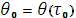
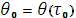 ;
; -
Значение начальной скорости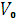
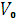 (обычно нулевое);
(обычно нулевое); -
Значение начального ускорения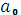
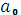 (обычно нулевое);
(обычно нулевое); -
Положение в точке ухода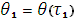
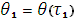 ;
; -
Непрерывность по положению в момент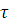
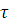 ;
; -
Непрерывность по скорости в момент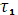
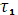 ;
; -
Непрерывность по ускорению в момент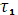
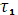 ;
; -
Положение в точке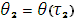
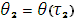 ;
; -
Непрерывность по положению в момент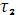
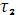 ;
; -
Непрерывность по скорости в момент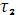
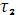 ;
; -
Непрерывность по ускорению в момент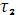
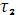 ;
; -
Конечное положение
 ;
; -
Значение конечной скорости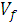
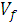 (обычно нулевое);
(обычно нулевое); -
Значение конечного ускорения
 (обычно нулевое).
(обычно нулевое).
Для расчета траектории берем второе звено с обобщенной координатой q2 = 120°.
Максимальное значение обобщенной координаты: q1max = 200°.
Находим значения присоединенных координат, исходя из условия, что: время прохождения 1-го участка траектории равно времени прохождения последнего участка траектории, и составляет 25% времени перемещения звена от начальной до конечной точки перемещения. Время прохождения 2-го участка в 2 раза больше времени прохождения 1-го участка.
Используя пакет программ Matlab, рассчитаем траекторию и построим для каждого участка траектории графики.
Рассчитываем первый участок траектории.
где
Тогда
Зная законы изменения положения, скорости и ускорения на первом участке, найдем поочередно значения функций на интервалеt
[0, 1] с шагом 0,1, и запишем данные в таблицу 2. Графики Пути, скорости и ускорения представлены на рисунках 6, 7 и 8 соответственно.
Таблица 2 – Значения функций положения, скорости и ускорения на первом участке
| t | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| | 12.05 | 12.38 | 13.23 | 14.78 | 17.08 | 20.21 | 24.04 | 28.54 | 33.72 | 39 |
| | 1.467 | 5.679 | 11.74 | 18.83 | 27.09 | 35.06 | 42.25 | 48.45 | 52.53 | 54 |
| | 28.94 | 54.78 | 67.93 | 77.59 | 81 | 77.59 | 67.93 | 54.78 | 28.94 | 0 |
Рассчитываем второй участок траектории.
Графики Пути, скорости и ускорения представлены на рисунках 9, 10 и 11 соответственно.
Таблица 3 – Значения функций положения, скорости и ускорения на втором участке
| t | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| | 44.39 | 49.79 | 55.18 | 60.57 | 66.06 | 71.46 | 76.8 | 82.19 | 87.59 | 93 |
| | 54 | |||||||||
| | 0 | |||||||||
Рассчитываем третий участок траектории.
Графики Пути, скорости и ускорения представлены на рисунках 12, 13 и 14 соответственно.
Таблица 4 – Значения функций положения, скорости и ускорения на третьем участке
| t | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| | 98.31 | 103.4 | 108 | 111.8 | 115 | 117.3 | 118.8 | 119.6 | 119.9 | 120 |
| | 52.2 | 48.28 | 42.25 | 34.96 | 27.02 | 18.84 | 11.75 | 5.644 | 1.448 | 0 |
| | -29.27 | -52.1 | -68.06 | -77.7 | -81 | -77.7 | -68.06 | -52.1 | -29.27 | 0 |
4. Динамический расчет манипулятора
Кинетостатический анализ основан на принципе Даламбера и заключается в определении усилий, развиваемых приводами робота, для реализации заданного движения манипулятора, а также для определения сил инерции в кинематических парах, возникающих при выполнении этого движения.
Рассчитанные усилия, развиваемые приводом, используются для абсолютного выбора двигателей привода. Силы и моменты сил инерции звеньев необходимы для расчетов манипулятора на прочность и жесткость.
Размыкаем кинематическую цепь манипулятора в третьей кинематической паре, представим это на рисунке 16, и составляем уравнения равновесия сил и моментов.
Дифференциальное уравнение крутящего момента:
Определим ускорение центра масс звена:
5. Определение точности и повторяемости позиционирования манипулятора
Положение центра схвата при максимальных обобщенных координатах:
Фактическое положение центра схвата в i – том рабочем цикле имеет координаты:
Таблица 5 – Фактические положения центра схвата
| № цикла | | | |
| 1 | 0.5703 | 1000.4942 | 0.5259 |
| 2 | 0.6341 | 1000.0222 | 0.1786 |
| 3 | 0.0889 | 1000.1938 | 0.3542 |
| 4 | 0.6394 | 1000.0323 | 0.4894 |
| 5 | 0.4427 | 1000.0679 | 0.6236 |
| 6 | 0.0689 | 1000.5764 | 0.6715 |
| 7 | 0.1949 | 1000.4863 | 0.3831 |
| 8 | 0.3828 | 1000.2219 | 0.097 |
| 9 | 0.6703 | 1000.6651 | 0.1045 |
| 10 | 0.6754 | 1000.0241 | 0.1803 |
| 11 | 0.1103 | 1000.3071 | 0.5885 |
| 12 | 0.6794 | 1000.2670 | 0.1780 |
| 13 | 0.67 | 1000.5358 | 0.5700 |
| 14 | 0.3398 | 1000.5566 | 0.1705 |
| 15 | 0.5602 | 1000.1308 | 0.6505 |
| 16 | 0.0993 | 1000.3428 | 0.2450 |
| 17 | 0.2952 | 1000.3119 | 0.1376 |
| 18 | 0.6410 | 1000.0452 | 0.1758 |
| 19 | 0.5545 | 1000.4965 | 0.4312 |
| 20 | 0.6716 | 1000.5282 | 0.3313 |
| 21 | 0.4590 | 1000.1932 | 0.2462 |
| 22 | 0.0250 | 1000.4757 | 0.5816 |
| 23 | 0.5944 | 1000.4585 | 0.4097 |
| 24 | 0.6538 | 1000.1138 | 0.3848 |
| 25 | 0.4751 | 1000.0832 | 0.6420 |
| 26 | 0.5304 | 1000.3488 | 0.2001 |
| 27 | 0.5202 | 1000.6718 | 0.5300 |
| 28 | 0.2746 | 1000.2382 | 0.5276 |
| 29 | 0.4588 | 1000.4096 | 0.2663 |
| 30 | 0.1198 | 1000.1566 | 0.3975 |