МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОНИКИ И МАТЕМАТИКИ.

(Технический университет)

Кафедра «Вычислительные системы и сети»

КУРСОВАЯ РАБОТА

НА ТЕМУ

«Проектирование многоразрядного десятичного сумматора комбинационного типа»
по дисциплине: «Теория автоматов»


Работу выполнил

Москва 2005

Исходные данные для проектирования.

Количество десятичных разрядов – 3.

Двоично-десятичный код, в котором находятся числа. – 8421+6.

Система логических элементов –И-НЕ.

Критерий оптимальности элементов для проектирования логических схем – минимальное количество логических элементов.

Тип триггера для проектирования схемы управления – JK.

Временные параметры синхронизирующей серии импульсов логических элементов:

Задержка 1 логического элемента – 1нс.

Длительность импульса – 2нс.

Промежуток между импульсами – 2нс.

Разработка алгоритма выполнения арифметических операций сложения и вычитания многоразрядных чисел в заданном двоично-десятичном коде.

8421+6	0	1	2	3	4	5	6	7	8	9
	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
0	1100	1101	1110	1111	0000	0001	0010	0011	0100	0101
0110	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
1	1101	1110	1111	0000	0001	0010	0011	0100	0101	0110
0111	0111	1000	1001	1010	1011	1100	1101	1110	1111	0110
2	1110	1111	0000	0001	0010	0011	0100	0101	0110	0111
1000	1000	1001	1010	1011	1100	1101	1110	1111	0110	0111
3	1111	0000	0001	0010	0011	0100	0101	0110	0111	1000
1001	1001	1010	1011	1100	1101	1110	1111	0110	0111	1000
4	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001
1010	1010	1011	1100	1101	1110	1111	0110	0111	1000	1001
5	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010
1011	1011	1100	1101	1110	1111	0110	0111	1000	1001	1010
6	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011
1100	1100	1101	1110	1111	0110	0111	1000	1001	1010	1011
7	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100
1101	1101	1110	1111	0110	0111	1000	1001	1010	1011	1100
8	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101
1110	1110	1111	0110	0111	1000	1001	1010	1011	1100	1101
9	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110
1111	1111	0110	0111	1000	1001	1010	1011	1100	1101	1110
Цветомвыделенаобласть, гденеобходимакоррекция:								Отсутствиепереноса
								Запрещеннаякомбинация

---

Величина коррекции одинакова для обеих областей и равна 1010.
Примеры:

---

Примеры с переполнением:

Разработка оптимальной схемы одноразрядного двоичного сумматора с учетом заданного базиса логических элементов.

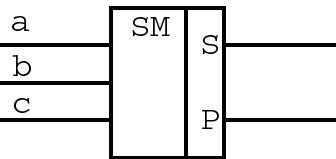
a	b	c	s	p
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

	a		¬a
b		1		1
¬b	1		1
	¬с	с		¬с

	a		¬a
b	1	1	1
¬b		1
	¬с	с		¬с

---

Логическая схема одноразрядного двоичного сумматора

---

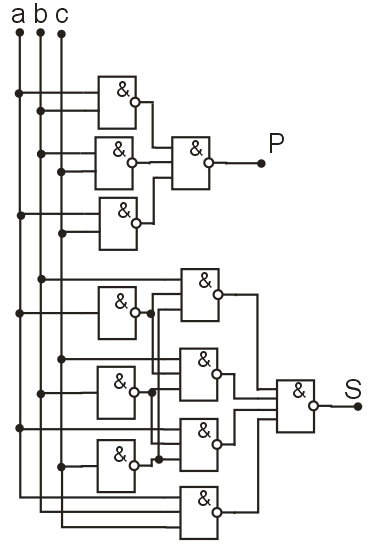
Разработка схемы коррекции.

Получим условие коррекции в случае запрещенной комбинации:

				Fзк
0	0	0	0	1
0	0	0	1	1
0	0	1	0	1
0	0	1	1	1
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

	4			не 4
3						1	не 1
						1	1
не3				1		1
				1		1	не 1
	не 2		2		не 2

---

Смотрите также файлы

• Экзаменационные вопросы по Теории вероятностей и математической статистике.docx

• Дискуссия в деловом общении как способ решения проблем.docx

• Кейс 16 крылова мария.pdf

• Конфликтология и медиация грузов игорь вячеславович.pptx

• Шекспир и шекспировский вопрос. Периодизация творчества.docx