Файл: Проектирование многоразрядного десятичного сумматора комбинационного типа.doc
Добавлен: 07.11.2023
Просмотров: 63
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Fk = (¬γ8)∙(¬γ2) + (¬γ8)∙(¬γ4) + Пi =
Разработка схемы одноразрядного двоично-десятичного сумматора.
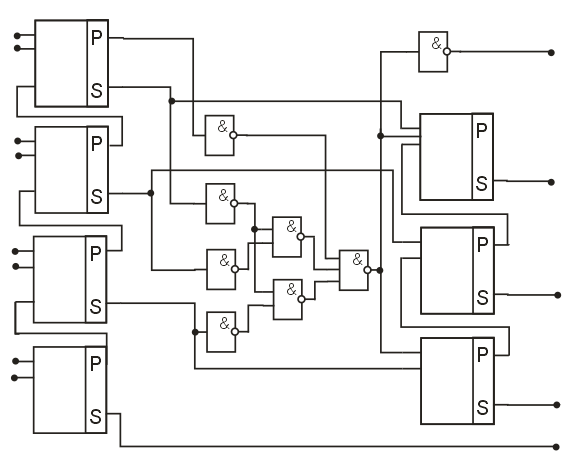
α8 Пi’
β8 Пi
α4
β4
γ8
α2
β2 Fk
γ4
α1
β1
γ2
γ1
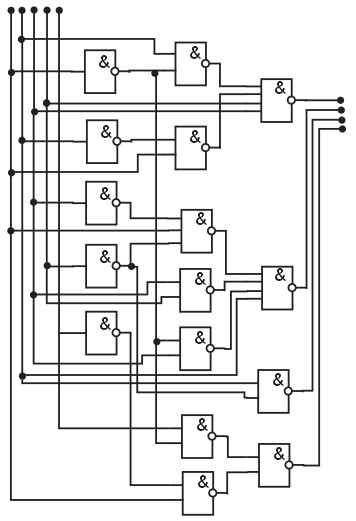
Разработка преобразователя прямого кода в обратный для работы с отрицательными величинами.
| a0 | a8 | a4 | a2 | a1 | a'8 | a'4 | a'2 | a'1 |
| 0 | 0 | 0 | 0 | 0 | x | x | x | x |
| 0 | 0 | 0 | 0 | 1 | x | x | x | x |
| 0 | 0 | 0 | 1 | 0 | x | x | x | x |
| 0 | 0 | 0 | 1 | 1 | x | x | x | x |
| 0 | 0 | 1 | 0 | 0 | x | x | x | x |
| 0 | 0 | 1 | 0 | 1 | x | x | x | x |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | x | x | x | x |
| 1 | 0 | 0 | 0 | 1 | x | x | x | x |
| 1 | 0 | 0 | 1 | 0 | x | x | x | x |
| 1 | 0 | 0 | 1 | 1 | x | x | x | x |
| 1 | 0 | 1 | 0 | 0 | x | x | x | x |
| 1 | 0 | 1 | 0 | 1 | x | x | x | x |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
Из таблицы сразу видны уравнения функций
. Остальные уравнения получаем с помощью диаграмм Вейча:| α1’ | 1 | ¬ 1 | | ||||||||||
| | 0 | ¬ 0 | 0 | ¬ 0 | | ||||||||
| 8 | | | 1 | 1 | 1 | 1 | | | ¬ 2 | ||||
| | | 1 | 1 | 1 | 1 | | | 2 | |||||
| ¬8 | x | | 1 | x | x | 1 | | x | |||||
| x | x | x | x | x | x | x | x | ¬ 2 | |||||
| | ¬ 4 | 4 | ¬ 4 | ¬ 4 | 4 | ¬ 4 | | ||||||
| α2’ | 1 | ¬ 1 | | ||||||||||
| | 0 | ¬ 0 | 0 | ¬ 0 | | ||||||||
| 8 | | | | | | | | | ¬ 2 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | |||||
| ¬8 | x | 1 | 1 | x | x | 1 | 1 | x | |||||
| x | x | x | x | x | x | x | x | ¬ 2 | |||||
| | ¬ 4 | 4 | ¬ 4 | ¬ 4 | 4 | ¬ 4 | | ||||||
α1’ =
α2’ =
| α4’ | 1 | ¬ 1 | | ||||||||||
| | 0 | ¬ 0 | 0 | ¬ 0 | | ||||||||
| 8 | 1 | | 1 | | 1 | | 1 | | ¬ 2 | ||||
| | 1 | 1 | | | 1 | 1 | | 2 | |||||
| ¬8 | x | 1 | 1 | x | x | 1 | 1 | x | |||||
| x | x | x | x | x | x | x | x | ¬ 2 | |||||
| | ¬ 4 | 4 | ¬ 4 | ¬ 4 | 4 | ¬ 4 | | ||||||
| α8’ | 1 | ¬ 1 | | ||||||||||
| | 0 | ¬ 0 | 0 | | 0 | ||||||||
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | | ||||
| 1 | | 1 | 1 | 1 | | 1 | 1 | | |||||
| ¬8 | x | 1 | | x | x | 1 | | x | |||||
| x | x | x | x | x | x | x | x | | |||||
| | ¬ 4 | 4 | ¬ 4 | | ¬ 4 | 4 | ¬ 4 | ||||||
α4’ =
α8’ =
Разработка схемы, фискирующей переполнение
|
|  φ = Приводим в базис «и - не» φ = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Функциональная схема, фиксирующая переполнение
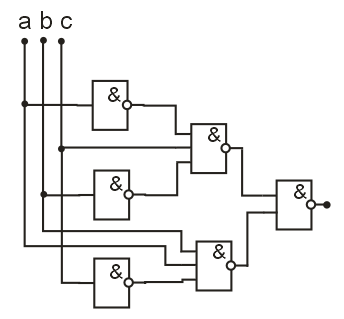
φ
Условное изображение этой функциональной схемы будет следующим
