Добавлен: 02.02.2019
Просмотров: 5538
Скачиваний: 25

39
ТЕОРИЯЛЫҚ СҰРАҚТАР
•
Үйлесімді жəне үйлесімсіз жүйе деп қандай жүйені
айтамыз?
•
Қай кезде жүйе анықталған деп аталады?
•
Жүйе шешудің Крaмер əдісін түсіндір.
•
Жүйе шешудің матрицалық əдісін түсіндір.
•
Жүйе шешудің Гаусс əдісін түсіндір.
•
Жүйенің базистік шешімдері дегеніміз не?
40
b
a
−
b
a
ҮШІНШІ ЛЕКЦИЯ
ВЕКТОРЛЫҚ КЕҢІСТІК
Негізгі ұғымдар. Мектеп курсынан белгілі векторлар
жөніндегі білімімізді жалпылайық.
Басы А, соңы В нүктесі болатын бағытталған кесінді
вектор деп аталады. Оқулықтарда векторларды
→
АВ
немесе
_
АВ
,
кейде тек қалың əріптермен АВ белгілеу түрлері кездеседі. Сол
сияқты векторларды бір əріппен де белгілей береді (
→
а
=
→
АВ
,
_
а
, а).
→
АВ
векторының ұзындығы деп АВ кесіндісінің ұзындығын
айтады жəне
→
АВ
деп белгілейді.
Басы мен соңы беттесетін вектор нолдік вектор деп
аталады,
→
0
=
→
АА
жəне ұзындығы нолге тең.
Бір түзудің не өзара параллель түзулер бойында орналасқан
векторлар коллениар векторлар деп аталады.
_
а
жəне
_
b
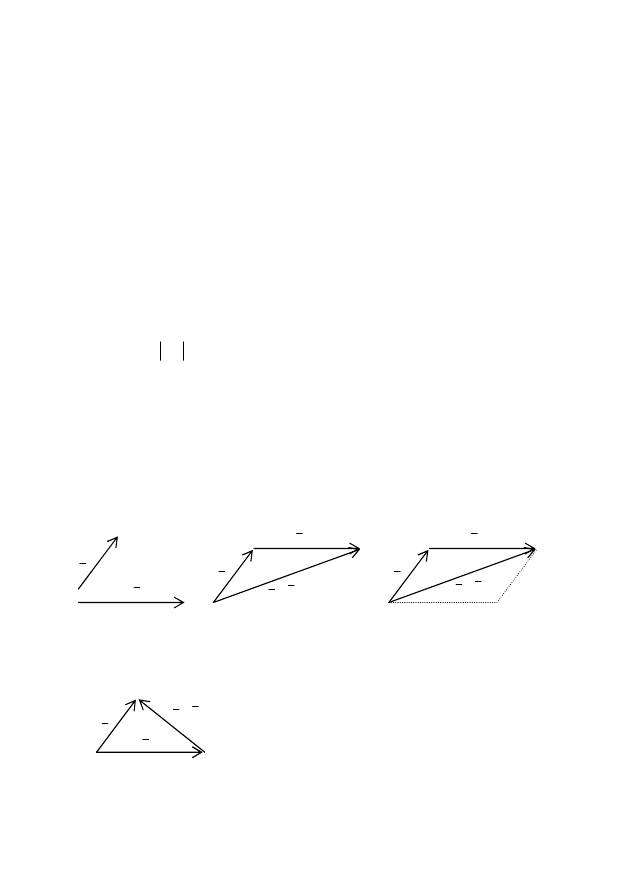
векторларының қосындысы «үшбұрыш» не
«параллелограмм» ережесімен анықталады:
_
а
жəне
_
b
векторларының
_
а
-
_
b
айырымы деп
_
b
-ға қосқанда
_
а
векторы алынатын
_
с
=
_
а
-
_
b
векторын
айтады.
b
a
+
b
a
b
a
+
b
a
b
a
41
A
y
2
y
1
0 x
1
x
2
x
B
_
а
векторының
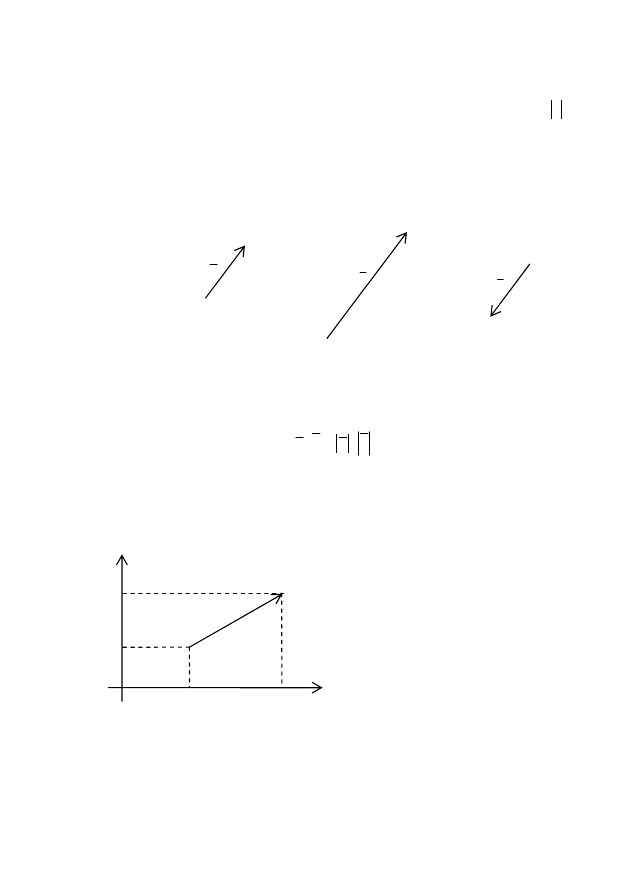
λ
санға көбейтіндісі деп ұзындығы
_
а
⋅
λ
болатын, бағыты
λ
>0 болғанда
_
а
векторымен бағыттас,
λ
<0
болғанда
_
а
векторымен қарама-қарсы бағытта болатын
_
b
векторын айтады. Суретте,
λ
= 2,
_
b
=2
_
а
;
λ
= -1,
_
b
=-
_
а
.
Екі вектордың скаляр көбейтіндісі деп осы векторлардың
ұзындықтары мен олардың арасындағы бұрыштың косинусына
көбейтіндісіне тең шаманы айтады:
ϕ
cos
b
a
b
a
⋅
=
⋅
.
Тік бұрышты декарт координаталар жүйесінде
_
АВ
векторының басы мен соңының координаталары белгілі болсын
)
,
(
1
1
y
x
A
жəне
)
,
(
2
2
y
x
В
. Сонда
_
АВ
векторын координаталары
арқылы былай жазуға болады:
_
АВ
=
)
,
(
1
2
1
2
y
y
x
x
−
−
_
АВ
векторының басы
координаталар
басымен
беттесетіндей етіп өз-өзіне параллель көшірсек, онда
_
АВ
векторының
координатасы
вектордың
соңының
координаталарымен бірдей болатынын аңғару қиын емес.
a
−
a
2
a
42
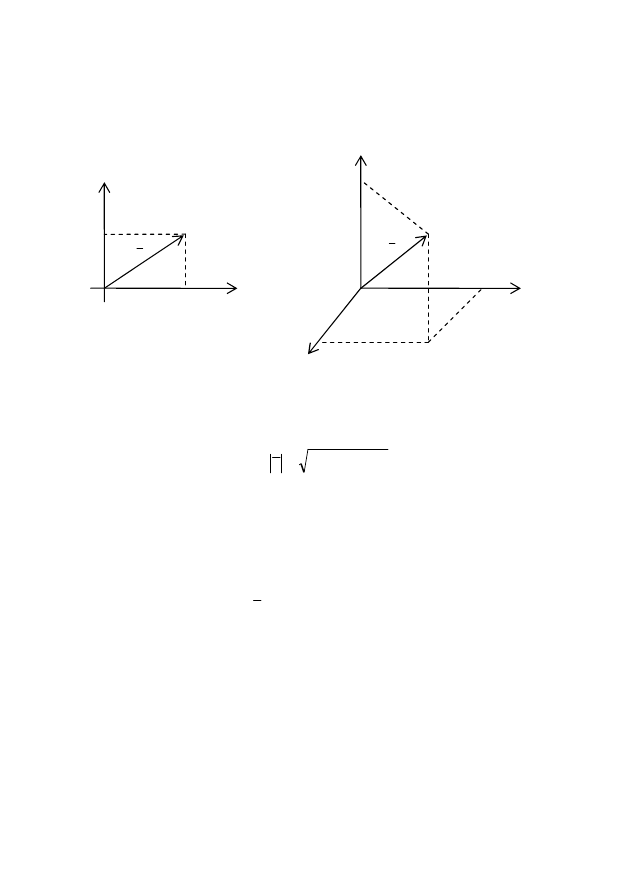
Жазықтықта вектордың координатасын екі сан анықтаса,
айталық
)
,
(
2
1
_
a
a
а
=
, кеңістікте үш сан анытайды,
)
,
,
(
3
2
1
_
a
a
a
а
=
.
Вектордың
ұзындығы
оның
координаталарының
квадраттарының қосындысынан алынған квадрат түбірге тең:
2
3
2
2
2
1
a
a
a
a
+
+
=
.
)
,
,
(
3
2
1
_
a
a
a
а
=
жəне
)
,
,
(
3
2
1
_
b
b
b
b
=
векторлары
координаталарымен берілген болса олардың қосындысы мынадай
түрде анықталады:
)
,
,
(
3
3
2
2
1
1
_
b
a
b
a
b
a
b
а
+
+
+
=
+
Ал
)
,
,
(
3
2
1
_
a
a
a
а
=
векторын
λ
санға көбейту мынадай түрде
анықталады:
)
,
,
(
3
2
1
_
a
a
a
а
λ
λ
λ
λ =
Ал
)
,
,
(
3
2
1
_
a
a
a
а
=
жəне
)
,
,
(
3
2
1
_
b
b
b
b
=
векторларының скаляр
көбейтіндісі мынадай:
a
a
2
y
a
1
x
z
a
3
a
1
x
a
a
2
y

43
3
3
2
2
1
1
_
b
a
b
a
b
a
b
а
⋅
+
⋅
+
⋅
=
⋅
Енді векторлық кеңістік ұғымына көшейік. Элементтері x,
y, z, … болатын қандай да бір R жиын қарастырайық. Осы
жиынның кез келген x жəне y элементтері үшін қосу x + y амалы
мен қандай да бір х элементі жəне
λ
нақты сан үшін көбейту
λ
х
амалы орындалсын.
Анықтама. R жиынның элементтерін қосу жəне
элементін нақты санға көбейту амалдары төмендегідей
шарттарды қанағаттандырса, R жиын векторлық (сызықтық)
кеңістік деп, ал элементтерін векторлар деп атайды:
1.
x+y=y+x;
2.
(x+y)+z=x+(y+z);
3.
Кез келген x
∈
R үшін 0
∈
R (нол-элемент) табылады да,
мынадай қатынас орындалады: x+0=x;
4.
Кез келген x
∈
R үшін -х
∈
R (қарама-қарсы элемент)
табылады да, мынадай қатынас орындалады: x+(-x)=0;
5.
⋅
1
x=x;
6.
λ
(
µ
x)=(
λ µ
)x;
7.
λ
(x+y)=
λ
x+
λ
y
8.
(
λ
+
µ
)x=
λ
x+
µ
x.
x жəне y векторларының айырмасы деп х векторы мен –1у
векторларының қосындысын айтамыз:
x-y=x+(-1)y
Векторлық кеңістіктің анықтамасынан кез келген х
векторды 0 нақты санына көбейткенде пайда болатын жалғыз
0 - ноль вектордың бар болатындығы; əрбір х вектор үшін осы
векторды (-1) санына көбейткенде пайда болатын жалғыз
қарама-қарсы ( –х) вектордың бар болатындығы шығады.
ВЕКТОРЛЫҚ КЕҢІСТІКТІҢ ӨЛШЕМІ ЖƏНЕ БАЗИСІ
R
сызықты кеңістіктің векторлары x, y, z, …, u болсын.
Мынадай
v=
α
x+
β
y+
γ
z+…+
λ
u