Файл: Виды и методы технического контроля качества продукции пао Среднеуральский медеплавильный завод.docx

База данных реализована на отдельном высокопроизводительном персональном компьютере. Весь технологический процесс (програм­мное управление и непрерывное регулирование) осуществляется ми­кроконтроллером.

---

2.2 Организация и управление техническим контролем и качеством продукции ПАО «СУМЗ»

Структура алгоритмизации рафинирования меди связана со стоха­стическими данными о химическом составе черновой меди и может быть представлена двумя подсистемами: подсистема подготовки пред­ложения для управления основными стадиями рафинирования и рас­четно-прогностическая подсистема. В свою очередь расчетно-прогно­стическую подсистему условно можно представить как оптимизация, прогнозирование поведения параметров аппроксимирующей функ­ции и параметрический синтез.

Алгоритмизация расчетно-прогностической подсистемы обеспечи­вает реализацию трех основных задач:

оптимизация состава шихты;

расчет теоретически потребной концентрации кислорода для окисления примесей и анализ аналитической зависимости;

расчет параметров восстановительной стадии.

Все задачи представляют собой логически связанные частные моде­ли. Декомпозиция модели проводится по однородным компонентам в пределах одной задачи. Правилом перехода к новой частной модели является адекватность предыдущей модели. Все данные о расчетных показателях частных моделей заносятся в базу данных.

Первая задача успешно решается методом линейного программиро­вания. Исходными данными для решения задачи могут быть текущие значения химического состава черновой меди, используемой в соста­ве шихты от нескольких заводов, либо значения химического состава черновой меди из базы данных (см. рис. 5).


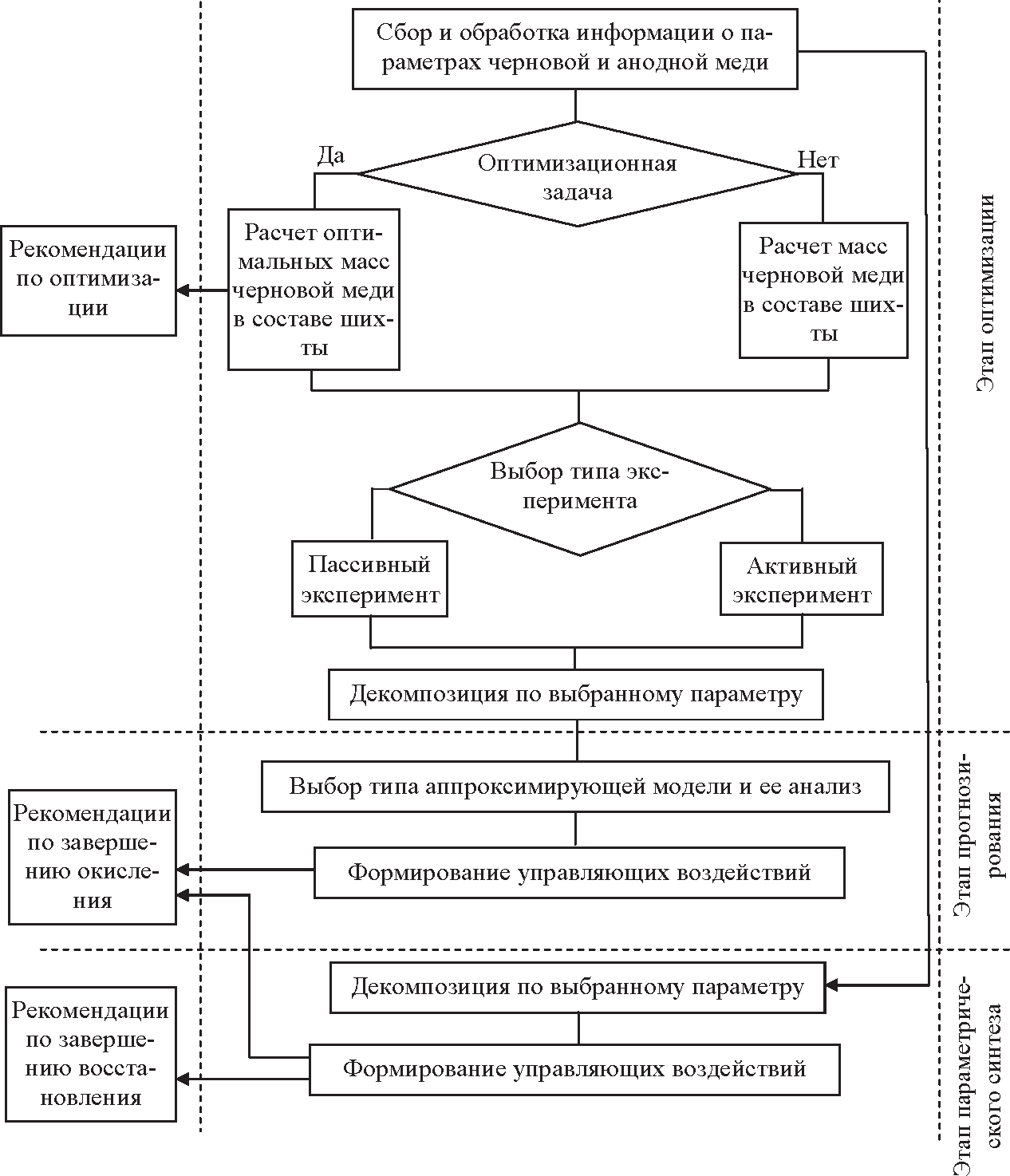
Рисунок 5 - Структура алгоритмизации огневого рафинирования меди

В качестве значений ограничений (bj) по каждому элементу в составе шихты предлагается несколько вариантов их расчета, например, сред­нее арифметическое значение элемента от всех заводов.

Далее составляется наилучший план, реализуя поиск значений пе­ременных x1, ..., xn, обращающих в минимум значение целевой функ­ции (см. формулу (5.3)). Целевая функция определяет оптимальный состав шихты, удовлет­воряющий условиям минимального содержания примесей в шихте.

Математическая модель была представлена системой линейных ал­гебраических уравнений (СЛАУ) (5.6).

---

После решения системы (5.6) с использованием данных о разовой загрузке печи находится оптимальный состав шихты с минимальным содержанием в ней примесей.

Анализ результатов показывает, что СЛАУ является совместной и определенной, так как для нее существует единственное решение, что является оценкой адекватности целевой функции.

В качестве рекомендаций, интегрированных в систему поддержки принятия решений, используются значения оптимальных масс черно­вой меди (т) в составе шихты от каждого завода, соответствующие ми­нимальному количеству примесей при заданном химическом составе шихты и определенных допущениях.

Для решения второй задачи используются результаты расчета, по­лученные на первом этапе.

Анализ экспериментальных данных показывает, что концентрация кислорода в расплаве зависит от температуры расплава, концентрации примесей, гидродинамики продувки жидкой ванны (Х1, Х2, ХД. Дан­ная зависимость, исследуемая в небольших интервалах, носит линей­ный характер и может быть описана уравнением множественной ли­нейной регрессии:

Y = b0 + b1X1 + b2X2 + ... + bnXn. (1)

При решении уравнений такого типа целесообразно использовать корреляционно-регрессионный метод, существенным образом упро­щающий оценку влияния переменных Хп на результативную перемен­ную Y.

Исходя из реальной исследовательской задачи подбирается необ­ходимое количество вариантов оценки корреляционной зависимости и формируется уравнение регрессии.

В случае оценки совместного влияния переменных Х1, Х2, Х3 на ре­зультативную переменную Y вводится множественный коэффици­ент корреляции R и формулируется нулевая гипотеза: переменные Х1, Х2, Х3 не оказывают влияния на концентрацию кислорода в расплаве.

Задача декомпозиции уравнения множественной линейной регрес­сии осуществляется по результатам пассивного эксперимента, с помощью которого выделим необходимое количество переменных в преде­лах статистической выборки. Значение коэффициента множественной корреляции рассчитывается по парным коэффициентам корреляции между значениями величин уравнения.

Недостаточность информации, полученной при расчете коэффи­циента множественной корреляции, позволяет выбирать параметры, влияющие на результативную переменную Y, на основе оценки их вза­имного влияния друг на друга.

---

Алгоритм оценки основан на вычислении парных коэффициен­тов корреляции и их значениях: | r | > 0,85 и | r | < 0,3, либо интервала от 0,7 до 0,99.

При | r | > 0,85 параметр оказывает существенное влияние на резуль­тативную переменную, и его необходимо учитывать при составлении уравнения. В противном случае (| r | < 0,3) параметр не оказывает су­щественного влияния на результативную переменную и его можно не учитывать при составлении уравнения.

Аналогично оценивается взаимное влияние между параметрами. При | r | > 0,85 нет смысла включать оба параметра в уравнение регрес­сии, так как один параметр очень сильно повторяет динамику другого параметра. В этом случае в уравнение регрессии включается тот, ко­торый оказывает большее влияние на Y.

Анализ оценки взаимного влияния переменных позволяет выбрать две переменные — концентрацию примесей и гидродинамику продув­ки жидкой ванны. В результате уравнение множественной регрессии можно записать в виде:

Y = b0 + b1X2 + b2X3. (2)

Стадия окисления характеризуется процессом удаления примесей за счет кислорода, подаваемого в расплав в составе воздуха.

Для анализа проводятся предварительные расчеты, представляю­щие отдельные наблюдения, по которым необходимо выявить и опи­сать общие закономерности. По известным данным химического соста­ва черновой меди для каждой плавки последовательно рассчитываются: масса (т) примесей в шихте, масса (т) Cu2O, необходимая для удаления всех примесей; теоретическое значение массы необходимого кислоро­да; расчетное значение концентрации кислорода в расплаве для окисле­ния примесей, мас. %; количество воздуха (м 3), подаваемого в расплав.

Рассчитанные данные заносятся в массив данных. Алгоритм создания математической модели окислительной стадии рафинирования основан на методе пассивного эксперимента и на допущении о том, что физико­химический механизм, приводящий к зависимости концентрации кис­лорода в расплаве от количества примесей в составе шихты, известен.

Выбор количества данных влияет на оценку качества рассчитанного уравнения регрессии, по которому строится график зависимости кон­центрации кислорода (мас. %) в расплаве от массы (т) Cu2O.

При расчете неиспользованного количества кислорода (воздуха) Д[Ор] (ДУ) используется методика, применяемая для решении вто­рой задачи: расчет массы (т) Cu2O; расчет значения невостребован­ной

---

концентрации кислорода в расплаве, мас. %; количество возду­ха (м 3) (см. рис. 6).

Рассчитанное значение неиспользованного кислорода (воздуха) ин­тегрируется в расчеты второго этапа в качестве поправки, уменьшаю­щей подачу в расплав меди кислорода Д [Op] (ДУ, воздуха).

На основании результатов расчета вырабатываются рекомендации по особенностям прогнозирования проведения окислительной стадии и формируются управляющие воздействия, интегрированные в систе­му поддержки принятия решений в качестве рекомендаций по сокра­щению времени стадии окисления.

Данные из архива о выбранном химическом составе анодной меди используются для расчета количественных показателей восстанови­теля. В качестве критерия расчета используется значение «лишнего» восстановителя (ДСН4), на величину которого рекомендуется умень­шить его подачу в расплав меди и как следствие сократить продолжи­тельность стадии восстановления.



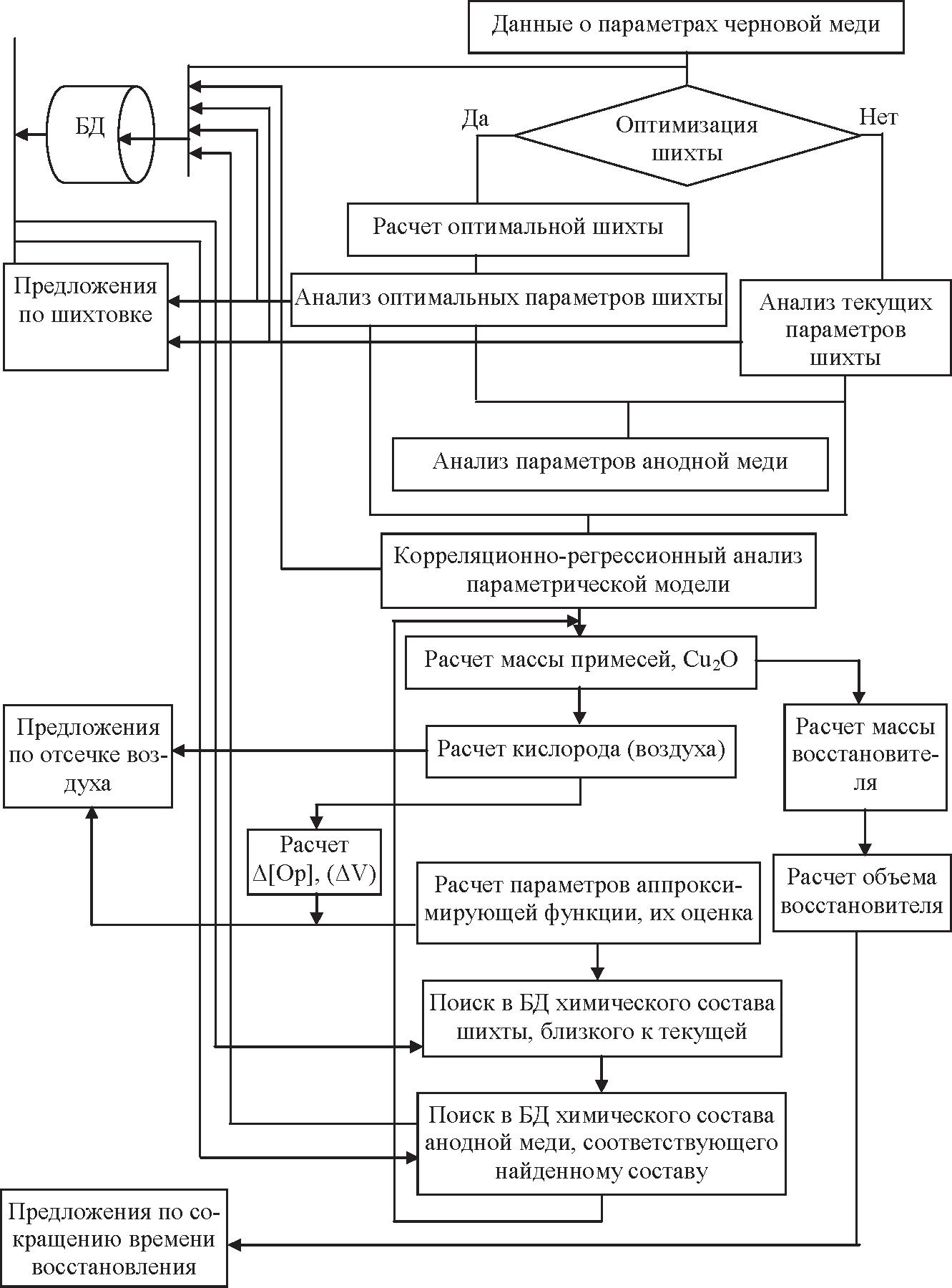
Рисунок 6 - Структура расчетно-прогностической подсистемы

Таблица 4 - Состав продуктов окисления, мас. %

Состав продуктов окисления, %	PbO	FeO	SnO	SiO2	AI2O3	NiO	ZnO	CuO
Начало окисления	20,1	2,5	16,3	18,5	28,9	2,3	8,2	3,2
Середина окисления	31,7	4,8	39,9	1,2	2,7	4	9	6,7
Конец окисления	31,8	4,9	35,4	0	0	4,3	6,5	17,1

---