Зерттеу жұмысын жасауда оқушының мақсаты – теориялық білімдерді тереңдету және ғылыми мәселелердің шешімдерін іздестіру әдістерін игерту. Оқушының бұл оқу-зерттеу жұмысы проблемалық оқумен тығыз байланысты. Оқушылардың ғылыми-зерттеу жұмысы оқушыны ғылыми зерттеуге баулудың неғұрлым жоғары дәрежесімен сипатталады және ол оқу үдерісінің шеңберіне сыймайды [10]. Оқушылардың ғылыми-зерттеу жұмыстарына талдау жасау келесідей кемшіліктердің кездесетінін көрсетті:

- оқушылар жалпы міндетті, зерттеуді өткізу мазмұнын және оның мақсатын толық түсінбейді, нысанды анықтауда, ғылыми зерттеу болжамын жасауда қиналады;

- жүйелі талдау жүргізе алмайды және материалдарды ғылыми-зерттеу жұмысы барысында қолдана алмайды;

- ғылыми-зерттеу әдістерін қолдануда қиналады;

- оқушыларда әдебиеттермен жұмыс істеу дағдылары толығымен қалыптаспаған;

- зерттеу барысында өзінің әрекетінің тиімді тиімсіз жақтарын көрсете алмайды.

Сонымен қатар, оқушыларды зерттеушілік іс-әрекетке баулуда мынадай сипаттамаларға көңіл бөлген жөн:

1. Жұмысты орындауға деген үлкен құлшыныс.

2. Жаңа білім, білік, дағдымен қарулануға деген ұмтылыс.

3. Сыни көзқараспен алынған ақпаратты талдауға, жинақтауға, болжам жасап оны ұсынуға, қорытындылауға және өз зерттеу қызметінде пайдалана отырып нәтиже шығаруға деген қабілеттілік.

4. Өз көзқарасын басқаның пікірімен сәйкес келмесе де дәлелдеуге талпыну [11].

Сонымен, оқушыларды зерттеушілікке үйретуде қолданылатын есептердің шығарылу формасын екі бөлімге бөлуге болады:

1. 
   Алгоритмдік және жартылай эвристикалық типтегі есептерді шығаруға үйрету.
   
2. 
   Эвристикалық типтегі есепті шығаруға үйрету.
   

Мұндай бөлу шартты екенін есте сақтаған жөн. Өйткені ғалымдардың зерттеулері бойынша кез келген типтегі есепті шығару жолдарын іздеу көп жағдайда бір-біріне ұқсас, «ізденістің, яғни эвристикалық әрекеттің мағынасы бар, егер есеп таныс және оны шешу жалпы жағдайда белгілі болса да» [12].

Осылар арқылы негізгі мектептегі білім берудің оқыту үдерісінде тек жаңа ақпарат іздеу немесе өңдеуден ғана емес, өз ойын жинақтап сол арқылы болжам жасап оны ұсына алу, алынған нәтижесін қорғай білуді талап ететін зерттеушілік әрекетті табысты жүзеге асыру барысында өз бетімен белсенді ізденістің әртүрлі деңгейі және оқушылар үшін қолжетімді зерттеу әдістерін қолдану арқылы оқушылардың танымдық белсенділіктері мен оқуға деген ынтасы артады.

2.2. 9 сынып геометриясын зерттеп оқыту технологиясын жүзеге асыру

---

Қазіргі таңда, математика сабағында оқушылардың шығармашылық қабілетін, танымдық ізденісін оқу-зерттеушілігін қалыптастыру үшін қандай да бір әдістемелік тәсіл құру керектігі айқын.

Зерттеушілік тапсырмаларды орындау кейде сабақтың бір ғана бөлігін қамтуы мүмкін. Оқушылардың зерттеушілік қызметі басқа қызметтермен үйлесіп кетеді. Ал, кейбір жағдайларда зерттеу жұмысы ұзақ уақытқа созылып, бірнеше сабақ бойы өткізілуі мүмкін.

Оқушыларды зерттеушілікке баулитын сабақтар бірқатар белгілермен сипатталады. Ол: проблемалық ахуал, оқушылардың ғылыми-зерттеу әдістерін қолдануы, жаңа білім алуда немесе өтілген материалды қайталауда оқушының өз бетінше жұмыс істеуі. Алайда қарастырылып отырған мәселенің сипаттылық ерекшеліктеріне қарай сабақ құрылымында елеулі өзгешеліктер де пайда болды. Әдетте, теориялық сұрақтарды зерттеу бірнеше сабақта қарастырылуы, ал кейбірі бір сабақтың өзінде-ақ сұрақтарға жауаптар табылып, ізденіс әрекеті аяқталуымүмкін.

Оқушылардың өз бетінше зерттеуқызметін ұйымдастыру және басқару үшін мұғалім өтуге тиісті оқу материалын алдын ала теориялық-логикалық талдау жасауы қажет және соның негізінде зерттеу жүргізу арқылы шешімі табылатын проблемалық ахуалдарды белгілейді.

Проблемалық ахуалды оқушылар игерген білім мен іскерліктің және түсіндіруге қажетті фактілер мен ұғымдардың арасындағы сәйкессіздік десек, онда проблемалық ахуалдың негізгі көзі есеп шығару болып табылады. Есептерді шығару барысында оқушылардың ойлау қызметін шыңдауға қажетті зерттеушілік дағдылар дамытылады [13].

Оқушының зерттеуге құштарлығы шығармашылық ойлауды қалыптастырудың алғашқы кезеңі уәждемелік қызметке сәйкес келеді. Бұл жағдайда проблемалық ахуал субъектінің ішкі қарама-қайшылығының туындау шарты болып табылады. Проблемалық ахуалды белгілеп қою зерттеу нысанының проблемаларын қалыптастырумен аяқталады [14].

Оқу-зерттеу жұмысы барысында оқушыларға ұсынылатын тақырыптарды таңдау барысында критерилерді таңдауға ерекше назар аудару қажет.

М.З. Каплан зерттеу әдісі бойынша критерилерді таңдаудың үш түрін қарастырған:

1. Фундаментальды критерийлер.

2. Белгілі бір деңгейге қатысты жүргізілетін зерттеуге арналған тақырыпты таңдау критериі.

3. Сабақтың типіне немесе сабақтың кезеңдеріне қатысты (сұрау, жаңа, тақырыпты түсіндіру, бекіту, бір кезеңнен екінші кезеңге өту) немесе сабақтың типіне байланысты [15].

Қарастыратын тақырыптар бойынша зерттеу іс-әрекетіне оқушыларды үйрету жалпы математикалық заңдылықтарды іздестіру мен оларды репродуктивтік, іздеушілік және шығармашылық деңгейде қолданудың алғышарттарын (негізгі қажетті ұғымдарды енгізу жұмыстары) жасау мен деңгейлік есептерді орындату арқылы жүзеге асырылады.

---

Геометрия пәнінен 9 сынып оқушыларының оқу-зерттеу іс-әрекеттерін бағытты қалыптастыру критерийлеріне сәйкес таңдалған тақырыптардың кейбірінің үлгісін ұсынамыз (1-кесте).

1-кесте. Таңдалған тақырыптар үлгісі

№	Тараудың аты	Тақырыптар
1	Жазықтықтағы векторлар	1. Векторларға амалдар қолдану 2. Үшбұрыш ережесі 3. Тең векторлар 4. Белгісізді табу 5. Векторлар арқылы өрнекті құру
2	Жазықтықтағы түрлендірулер	1.Жазықтықтағы түрлендірулер. 2. Центрлік және осьтік симметрия.
3	Шеңбер және көпбұрыштар	1. Шеңберге іштей немесе сырттай сызылған үшбұрыштың ауданын пайдаланып шеңбердің радиусын табу 2. Шеңберге жүргізілген жанама 3. Дұрыс көпбұрыштарды салу және ауданын есептеу
4	Үшбұрышты шешу	1. Косинустар теоремасы 2. Синустар теоремасы 3.Синустар және косинустар теоремаларын үшбұрыштарды шешуде және қолданбалы есептерде қолдану.

«Векторларға амалдар қолдану» тақырыбын қарастырайық. Вектордың бағытталған кесінді екенін білетін оқушы үшін бұл тақырып қатты таңданысты тудырмауы мүмкін. Алайда бағыттаушы мұғалім оларға: векторларды сандар сияқты қосуға және азайтуға болады ма? Егер бар болатын болса, (бұл кезде мұғалім тақтаға 7 сыныпта өтілген фигураларды яғни, үшбұрыш және параллелограммды салып қойып) мына суретке назар салайық. Бұл қандай фигура еді? Оқушылар тақтадағы фигуралар мен векторлардың қандай байланысы бар екендігін білуге қызығушылығы артар еді. Осылайша, олар ойындағы бірінші жауапты береді: үшбұрыш және параллелограмм. Бұл жауаптың дұрыстығы белгілі, десек те оның векторлармен байланысы қандай екендігі оқушылар үшін беймәлім дүние.

Осы кезде мұғалім бағыттаушы қызметін атқарып, жаңа тақырыпты түсіндіру барысында оларға барлық теорияларды өзі айтып бермейді, оның атқаратын қызметі тек белгілі қадамдармен жұмыс жүргізу арқылы оқушының сол қадаммен жүріп өтуіне жағдай жасау және оны өзі қадағалау. Осыған байланысты жаңа тақырыпты игертуде оқушының ішкі қорқынышын кетіріп, ауызша көмек беру арқылы оқушының өзінің қабілетіне жол ашады.

---

Үшбұрыш ережесі. Бұл тақырыпты индуктивті ашуға болады. Индуктивті қорытынды жасау ол дәлелдеу емес екенін естен шығармау керек: ол дегеніміз жеке қадамдарды орындау арқылы нақты ережені шығару.

Мұғалім-бағыттаушы: Үшбұрыш ережесіне сәйкес 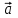және 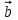екі векторды қосу үшін мына әрекеттерді орындаңыздар:

• 
  кез келген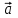 векторын салыңыз (мұнда оқушылар алдыңғы тақырыппен байланыстырып, яғни 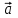векторын салу үшін кез-келген нүктені таңдап алу керектігі және осы нүктеден бастап берілген 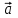векторына тең вектор салуды біледі);
  
• 
  алынған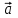 векторының ұшынан бастап 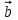векторына тең вектор салыңыз (вектордың басы және ұшы деген ұғымды ажырата алады);
  
• 
  енді берілген екі векторды қолдана отырып, үшбұрышқа толтырыңыз. (мұндағы үшбұрыштың екі қабырғасы сәйкесінш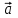е және 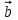векторлары, ал үшінші қабырғасы олардың қосындысы екендігін олар түсінеді).
  

Ескерту. Бір оқушы 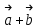деп жазса, енді бірі 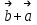деп жазатыны күмәнсіз. Бірақ бұл жерде векторларды қосу амалының қасиеті ауыстырымдылық заңы орын алғанмен де екі векторды қосу ережесінің яғни үшбұрыш ережесінің басты шарты: бірінші вектордың басы мен екінші вектордың ұшын қосу керектігі олардың санасында әлі көрініс тапқан жоқ. Мұны атап өту маңызды. Сондықтан оларға жадыда жақсы сақталу мақсатында мына ассоциациялық формуланы ұсынуға болады: Қ = Б₁ + Ұ₂ (мұндағы, Б₁ – бірінші вектордың басы, Ұ₂ – екінші вектордың ұшы және Қ -қосынды).

Сол секілді проблемалық есепті беру арқылы оны шығару барысында үшбұрыш ережесін пайдаланып, бірнеше вектордың да қосындысын салуға болады. Мысалы, 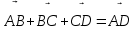. Ол үшін келесі вектордың басын алдыңғы вектордың ұшына сәйкес келетіндей етіп салу керектігін оқушылар өз бетімен аңғарып, яғни бірінші вектордың басын екінші вектордың ұшымен қосатын вектор осы векторлардың қосындысы болады деген тұжырымға келеді. Параллелограмм ережесін осы секілді дәлелдеуге өз бетімен жұмыс ретінде қалдыруға болады.

---

Бұл проблемалық есептің бірден-бір алғышарты ретінде жасалынған қадамдар жаңа білімді алудың қажет екені туралы қызығушылық туғызады, себебі оқушыларға дайын есепті бермей тек мұғалімнің берген нұсқаулығын қолдану арқылы белгісіз тақырыпты алдыңғы өтілген тақырыптармен байланыстыра отырып, оқушылардың өзіндік белсенділігі мен қызығушылығын арттыруға, ғылымда ашылған бірақ өздері үшін ашылмаған тақырыптың мәні мен мағынасын түсінуге үлкен көмегін тигізеді.

Векторларды азайту ережесінде де осылай жоғарыдағы қадамдар секілді ұқсастығы мен ерекшелігі айқындалып оқушылардан сөзімізге дәлел ретінде мынадай ассоциациялық формуланы алуымызға болады: А = Ұ₂ - Ұ₁ (мұндағы, Ұ₂ – екінші вектордың ұшы, Ұ₁ – бірінші вектордың ұшы және А -азайту).

Векторларға амалдар қолдану тарауына байланысты оқушылардың қызығушылығын арттыруда зерттеу іс-әрекетіне бағыттайтын төмендегідей сұрақтарды қоюға болады :

• 
  Векторларды қосудың параллелограмм ережесі бойынша әрекеттер ретін кім көрсеткісі келеді?
  
• 
  Векторларды тізбектеп қосу арқылы тұйық сынық сызық шықса (алғашқы вектордың басы мен соңғы вектордың ұшы беттессе), бұл векторлардың қосындысы нені береді? (нөлдік вектор).
  
• 
  Параллелограмм ережесін векторларды азайтуда қолдануға болады ма?
  
• 
  Екі вектордың айырымы деп қандай векторды айтуға болады?
  
• 
  Параллелограмның қай диагоналі параллелограмның іргелес қабырғаларында жатқан векторлардың қосындысын анықтайды?
  

Оқушылардың танымдық қызметін дамытуға бағытталған, векторларға қолданылатын амалдардың қасиеттеріне сүйене отырып, өз бетімен орындауға берілетін есептер мысалдарын қарастырайық:

---

Смотрите также файлы

• С ocacola classic (классическая кола).docx

• Курс на ускорение развития общества середины 1980х годов.docx

• Ваучерная приватизация особая форма безвозмездной приватизации государственной собственности по принципу "дележки" государственной собственности, предназначенной для приватизации, между всеми трудящимися.docx

• Существование общества невозможно без постоянного производства материальных благ и услуг.docx

• Благодаря своей относительной простоте применения, быстроте соединения различных материалов сварка находит широкое применение.docx