Файл: Образовательная программа Компьютерный анализ и интерпретация данных к защите допустить Зав каф. Сиб.docx

2.2. Регистр сдвига с линейной обратной связью

Регистр сдвига с линейной обратной связью (РСЛОС) – это алгоритмический ГПСЧ, использующий регистр сдвига для генерации последовательности битов.

Регистр сдвига – это цепочка триггеров, соединенная последовательно. Он хранит определенное количество битов и выполняет операцию сдвига разрядов двоичного кода, записанного в триггеры [6], на один бит вправо или влево (рис. 2.1).



Рис. 2.1. Линейный сдвиговый регистр с обратной связью

Также в РСЛОС используется линейная обратная связь между битами регистра, то есть каждый бит регистра вычисляется как линейная комбинация предыдущих битов с некоторыми коэффициентами. Например, для регистра из трех битов коэффициенты могут быть следующими: 1, 0, 1.

Таким образом, каждый новый бит регистра вычисляется как XOR двух предыдущих битов, умноженных на соответствующие коэффициенты.

Пусть последовательность битов [????₁, ... ,????_????] задает конфигурацию отводной последовательности. Отводам в данной последовательности будут соответствовать единицы, тогда как всем оставшимся ячейкам – нули.

Содержимое регистра сдвига обозначим [????_????−1, ... , ????₀].

Шаг генерации каждого очередного бита при помощи регистра сдвига длины l описывается следующими операциями:

1) проводится вычисление результата функции обратной связи (например, XOR ячеек регистра с коэффициентами ????₁, ... , ????_????);

2) результат записывается в крайнюю слева ячейку регистра (????_????−1);

3) производится сдвиг вправо на одну позицию всех битов регистра;

4) содержимое крайней̆ справа ячейки регистра (????₀) будет образовывать выходное значение генератора.

(2.2)

К основным достоинствам [11] генераторов типа РСЛОС можно отнести простоту реализации и относительно высокую скорость работы.

---

Последовательность битов, получаемая генератором, может быть использована для создания ПСЧ путем разбиения последовательности на блоки и преобразования их в числа.

Однако, стоит отметить также и то, что РСЛОС имеет определенные ограничения, такие как короткий период генерации и возможность предсказания следующего числа в последовательности при известных начальных значениях регистра.

Генераторы типа РСЛОС играют важную роль не только непосредственно в генерации ПСЧ, но также и в различных аспектах защиты данных.

Такими аспектами являются, например, контроль целостности данных (CRC-коды), самотестирование интегральных схем, разработка криптографических алгоритмов и другие [5, 9-11, 14, 16].

2.3. Алгоритм «Вихрь Мерсенна»

Алгоритм «Вихрь Мерсенна» (от англ. Mersenne Twister) был разработан двумя японскими учеными Такэро Нисимура и Макото Матсумото.

Своим названием алгоритм обязан так называемым простым числам Мерсенна, то есть числам вида

Mn=2n-1

(2.3)

, где n – это натуральное число. Основой алгоритма является число Мерсенна.

Существуют две основные версии данного алгоритма, различающихся размером использующегося числа Мерсенна [7]. Новейшая и наиболее распространённая модификация алгоритма называется MT19937.

Вихрь Мерсенна использует ЛКМ. Однако, для устранения ограничений ЛКМ (короткий период и низкая степень равномерности) Вихрь Мерсенна использует более сложный алгоритм, который основывается на использовании массива из 624 значений, каждое из которых является 32-битным целым числом. Каждый очередной элемент массива вычисляется на основе предыдущих элементов, а также определенных констант.

Вихрь Мерсенна обладает длинным периодом, высокой скоростью и относительно хорошей криптографической стойкостью, однако требует большого объема памяти для хранения массива чисел.

Будем обозначать x векторы-слова, которые представляют собой w-мерные векторы над полем F₂ = {0,1}, которые соответствуют машинному слову размера w.

Алгоритм генерирует последовательность данных вектор-слов, псевдослучайных целых и лежащих в диапазоне от 0 до 2^w – 1. Операцией деления на 2^w – 1 получится псевдослучайное вещественное значение из диапазона [0,1].

Основой алгоритма является следующее рекуррентное выражение:

---

(2.4)

Пояснение параметров рекуррентного выражения приведено в таблице 2.3.

Таблица 2.3

Параметры Алгоритма Вихрь Мерсенна

Параметр	Описание
k	Порядковый номер (шаг) операции
n	Степень рекуррентности. Целое
m	Целое. Ограничение: 1 ≤ m ≤ n
A	Матрица размера w×w с элементами из F2
|	Операция Побитовое ИЛИ (OR)
⊕	Операция Сложение по модулю 2 (XOR)
xku	«старшие» w-r бит xk
xk+1l	«младшие r бит» xk+1
Вектор (xku | xk+1l)	конкатенация старших w-r бит xk и младших r бит xk+1.

В качестве начального заполнения возьмем вектор (x₀, x₁,..., x_n-1). Тогда по рекуррентному выражению (2.4) генератор рассчитает x_n при k= 0.

Полагая, что k = 1,2, ..., w генератор вычислит x_n+1, x_n+2,..., x_w.

(2.5)

Вычисление xA сводится к следующим побитовым операциям:

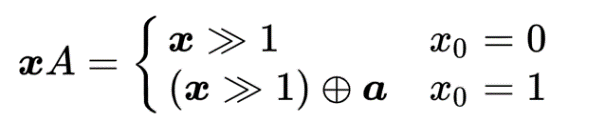(2.6)

---

, где x:= (xku| xk+1l ) k = 0,1,…;

a:= (aw-1, aw-2 , … a0 );

x:= (xw-1, xw-2 , … x0 );

Генерируемые рекурсией (2.4) необработанные последовательности имеют один важный недостаток – они обладают довольно плохим равномерным распределением на больших размерностях.

Для исправления данного недостатка используется так называемый метод закалки, результатом которого является итоговая псевдослучайная последовательность.

Суть метода закалки заключается в том, что каждое сгенерированное слово умножается справа на особую обратимую матрицу T размера w × w.

Для матрицы T: x → z = x T выбраны следующие последовательные преобразования:

y := x ⊕ (x >> u) y := :y ⊕ ((y << s) & b) y := :y ⊕ ((y << t) & c) z := y ⊕ (y >> l)

(2.7)

где l, s, t и u – целые числа,

а b и c — специально подобранные битовые маски размера слова,

(x≫u) обозначает побитовую операцию сдвига вправо на u бит.

В основе Вихря Мерсенна лежат две основных части: рекурсивная и закалки.

Рекурсивная часть реализуется с помощью РСЛОС. Все биты состояния в регистре определяются рекурсивно. Выходные биты определяются также рекурсивно, но на основе битов состояния.

Регистр сдвига состоит из 624 элементов, и в общей̆ сложности имеет 19937 клеток. Каждый элемент, кроме первого, имеет длину 32 бита. Первый элемент имеет только 1 бит за счет отбрасывания бита.

Процесс генерации начинается с применения битовой̆ маски, которая отбрасывает 31 бит (то есть все, кроме наиболее значащих битов). Далее происходит этап инициализации (x₀,x₁,..., x₆₂₃) любыми 32-разрядными беззнаковыми целыми числами.

Следующие шаги включают в себя объединение и переходные состояния.

Пространство состояний имеет 19937 бит (то есть 624 элемента по 32 бита, исключая 31 бит: 624 * 32 - 31). Следующее состояние генерируется сдвигом одного слова вертикально вверх и вставкой нового слова в конец. Новое слово рассчитывается посредством гаммирования.

Выходная последовательность начинается с x₆₂₄, x₆₂₅, ..., x₁₉₉₃₇.

Алгоритм (рис. 2.2) производится в 6 этапов.



Рис. 2.2. Алгоритм Вихря Мерсенна

Главными преимуществами Вихря Мерсенна перед другими ГПСЧ являются:

---

1) более быстрая скорость работы, чем у других генераторов, за исключением статистически-дефектных генераторов, поскольку при генерации не требуется проводить операции умножения и деления;

2) большой период;

3) отсутствие определенного шаблона в генерируемой последовательности чисел;

4) алгоритм статистически случаен во всех выходных битах.

Следует также отметить, что Вихрь Мерсенна имеет облегченную версию, которая адаптируется к ограничениям ресурсов, что значительно снижает требования к буферу за счет сокращения продолжительности периода [8].

---