Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 975

Скачиваний: 24

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Ответы на тесты

Выберите два варианта ответов

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №2

1. Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является…

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №3 Отметьте верные утверждения односторонние пределы всегда меньше двустороннего сумма и разность бесконечно большой величины и ограниченной функции есть бесконечно большая величина если существует двусторонний предел, то существует и односторонние пределы равные ему же если функция монотонна и ограничена, то она не имеет предел Предел произведения функций равен… бесконечно малой величине произведению пределов этих функций бесконечно большой величине это ситуация неопределенности Впишите правильный ответ Пусть f: X R, a-предельная точка множества Х. Если функция имеет конечный предел при окрестности точки a.x a, то онав некоторой проколотой Выберите неверное утверждение: Дана функция f(x)  . x lim x0 lim x 0 lim x 0 lim f (x) не существуетf(x)  1f(x)  1f(x)  1 x  0 Отметьте примеры, в которых переход к эквивалентным совершен верно: x arcsin2 x x0x2 ; tgx sin x x0x x; C) (x 3)  sin(x 1) (x 3)(x 1) ;x0D) x2  tg(  x) x2 (  x) x Вычислить: limх3  8 12 ∞ 4 -4 x2 аrсtg(x 2) Пусть  (x) и (x)являются бесконечно малыми функциями при x a. Что можно сказать о функцияхx a (x)   (x); (x)   (x); (x) (x)при Бесконечно малая; бесконечно малая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; бесконечно малая Бесконечно малая; бесконечно большая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; стремится к 1 Пусть f положительная бесконечно большая, а gотрицательная бесконечно большая функции при x a. Что можно сказать о функциях f g;f g;f приgx a бесконечно малая; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; бесконечно малая бесконечно малая; отрицательная бесконечно большая; бесконечно малая Установить соответствие между 1 цифрой и 1 буквой а) формула, определяющая второй замечательный предел 1 f(x1), f(x2), f(x3),… f(xn), состоящая из значенийфункции, сходится к числу А. б) формула первого замечательного предела 2 lim (1 1)x ex x в) число А называется пределом функции f(x)в точке х=х0, если для любой,сходящейся к х0последовательности x1,x2,x3,…xn…, состоящей из значений аргумента, отличных от х0,соответствующая последовательность 3 lim sin x 1x0 x г) если функция имеет областьопределения на всей числовой оси, то ее предел в точке равен 4 значению функции в этой точке Число А называется пределом функции в точке Х0, когда к Х0 сходится последовательность из значений а) аргументаб) числовой осив) координатной плоскости г) функции 1   2   3   4   5   6   7   8   9   ...   14

Ответы на тесты

Тест №1

Тест №3

Ответы на тесты

Тест №1

Тест №2

Ответы на тесты


МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования

«Саратовский государственный аграрный университет имени Н.И. Вавилова»

СБОРНИК ТЕСТОВ ПО МАТЕМАТИКЕ

Саратов-2016


Содержание

Тесты входного контроля по дисциплине МАТЕМАТИКА 3

Тест №1 3

Тест № 2 4

Тест № 3 5

Ответы на тесты 6

Тема “Предел функции” 7

Тест №1 7

Тест №2 9

Тест №3 11

Ответы на тесты 13

Тема “Нахождение производных функций.” 14

Тест №1 14

Тест №2 16

Тест №3 18

Ответы на тесты 19

Тема “Неопределенный и определенный интеграл/” 20

Тест №1 20

Тест №2 22

Тест №3 24

Ответы на тесты 26

Тесты входного контроля
по дисциплине МАТЕМАТИКА. Тест №1
Ответы

Задание
А
Б
В
Г


1.
Упростите выражение

5 32a7 5 a3
4a4
16a2
2a2
2a


2.
Найдите значение выражения

1 3 147 3 63

3

7

21

- 7

- 21


3.
Упростите выражение

3 1 1 1

3

a4 a4 : a2

 

a4

51

a12

a4

a3


4.
Найдите значение выражения

2

5 0 2 1 3

6 4

16 3 4

 

1

2,5

- 5

0


5.
Найдите значение выражения

2 log 3 log 1

6 6 4

2

2 log 6 0,75

1,25

1,5


6.
Решите уравнение и укажите верное утверждение о корнях

x 2 x 4
Корень только один, и он положительный
Корень только один, и он отрицательный
Корней два, и они

разных знаков
Корней два, и они положительные



7.
Укажите промежуток,

которому принадлежит корень уравнения

1 0,2 x1

25

125


3;9

7;0

9;7

0;3


8.
Найти область определения функции y0,42x1 0,16
1,5;
0,5;

;1,5
;0,5


9.
Какое из чисел входит в множество значений функции

y 4 2x

2

3

4

5

10.
Какая из функций является

чётной?
y x2 3x
y 8x4
y x2 cos x
y log 3 x
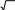
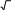
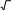
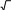
Тест № 2






Ответы
Задание
А
Б
В
Г


1.
Упростите выражение

5 2a7b3 5 16a2b28

2ab5

1

32ab5

32ab5

  • 2ab5


2.
Найдите значение выражения

4

33 3 16 3 48

33

6 6

43

6

0

3

6



3.
Упростите

1

9m3 m32

2

8

m3
выражение


2

27m3

27

2

3

m

27

3

m2


3

27m2


4.
Найдите значение выражения

1 3


27 2  1 4  1 4 3    

256 16

3 8

9
4 8

9
12 1

9
4 1

9

5.
Найдите значение выражения

log 15 log 5 3log3 5

3 3
6
2 2 log 7 2
2
3 6 log 7 2


6.
Решите уравнение и укажите верное утверждение о корнях

2x1 x 2
Корень только один, и он положительный
Корень только один, и он отрицательный
Корней два, и они разных

знаков
Корней два, и они положительные



7.
Укажите промежуток, которому принадлежит корень

уравнения 33x1 3x 1

3

2;0,5

1;1,8

2;4

5;10



8.
Найти область определения

1 3x1 1

функции y  

11 121

1,5;
;1
; 1

2




;1,5



9.
Какое из чисел входит в множество значений функции

1 x

y 5

3


3

7

5

4

10.
Какая из чётной?
функций является
y log 9 x 5
y x cos x
y x6 2
y x3 x

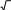
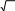
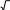
Тест № 3
Ответы
Задание
А
Б
В
Г


1.
Упростите выражение

3 4 4m6
2m2
2m

1

2m2
2m3


2.
Найдите значение выражения

3 81 490,5 3 24

143 3

3 33

113 3

- 11



3.
Упростите выражение

31

8k3 k2

21

k 2

8k7

8k4

8k8

8k9


4.
Найдите значение выражения

3 3

480 70 4 325

100

108

116

28


5.
Найдите значение выражения

log 144 2 log 1 1

6 6 2

6

log 6 144

3

37


6.
Решите уравнение и укажите верное утверждение о корнях

x 4 31 6x
Корень только один, и он положительный
Корень только один, и он отрицательный
Корней два, и они разных знаков
Корней два, и они положительные



7.
Укажите промежуток,

которому принадлежит корень уравнения

1 2 1

x

4 2

  8

3;4

1,5;2,5

1;1,5

0;1



8.
Найти область определения

1 2x1

функции y  

7 49

;1

1;
1;
;1


9.
Какое из чисел входит в множество значений функции y 4x 2

2

3

0

1


10.
Какая из функций является нечётной?
3

1  x

y   1

2

y log 2 x 2
y x cos x
y xsin x

Смотрите также файлы