Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 983

Скачиваний: 24

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Ответы на тесты

Выберите два варианта ответов

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №2

1. Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является…

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №3 Отметьте верные утверждения односторонние пределы всегда меньше двустороннего сумма и разность бесконечно большой величины и ограниченной функции есть бесконечно большая величина если существует двусторонний предел, то существует и односторонние пределы равные ему же если функция монотонна и ограничена, то она не имеет предел Предел произведения функций равен… бесконечно малой величине произведению пределов этих функций бесконечно большой величине это ситуация неопределенности Впишите правильный ответ Пусть f: X R, a-предельная точка множества Х. Если функция имеет конечный предел при окрестности точки a.x a, то онав некоторой проколотой Выберите неверное утверждение: Дана функция f(x)  . x lim x0 lim x 0 lim x 0 lim f (x) не существуетf(x)  1f(x)  1f(x)  1 x  0 Отметьте примеры, в которых переход к эквивалентным совершен верно: x arcsin2 x x0x2 ; tgx sin x x0x x; C) (x 3)  sin(x 1) (x 3)(x 1) ;x0D) x2  tg(  x) x2 (  x) x Вычислить: limх3  8 12 ∞ 4 -4 x2 аrсtg(x 2) Пусть  (x) и (x)являются бесконечно малыми функциями при x a. Что можно сказать о функцияхx a (x)   (x); (x)   (x); (x) (x)при Бесконечно малая; бесконечно малая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; бесконечно малая Бесконечно малая; бесконечно большая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; стремится к 1 Пусть f положительная бесконечно большая, а gотрицательная бесконечно большая функции при x a. Что можно сказать о функциях f g;f g;f приgx a бесконечно малая; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; бесконечно малая бесконечно малая; отрицательная бесконечно большая; бесконечно малая Установить соответствие между 1 цифрой и 1 буквой а) формула, определяющая второй замечательный предел 1 f(x1), f(x2), f(x3),… f(xn), состоящая из значенийфункции, сходится к числу А. б) формула первого замечательного предела 2 lim (1 1)x ex x в) число А называется пределом функции f(x)в точке х=х0, если для любой,сходящейся к х0последовательности x1,x2,x3,…xn…, состоящей из значений аргумента, отличных от х0,соответствующая последовательность 3 lim sin x 1x0 x г) если функция имеет областьопределения на всей числовой оси, то ее предел в точке равен 4 значению функции в этой точке Число А называется пределом функции в точке Х0, когда к Х0 сходится последовательность из значений а) аргументаб) числовой осив) координатной плоскости г) функции 1   2   3   4   5   6   7   8   9   ...   14

Ответы на тесты

Тест №1

Тест №3

Ответы на тесты

Тест №1

Тест №2

Ответы на тесты

Ответы на тесты





Тест №1

№

задания
1
2
3
4
5
6
7
8
9
10

Ответ
В
А
Г
А
А
А
В
В
Г
В

Тест №2

№

задания
1
2
3
4
5
6
7
8
9
10

Ответ
А
Б
А
А
А
А
А
Б
А, Г
В

Тест № 3

№

задания
1
2
3
4
5
6
7
8
9
10

Ответ
Б
В
Г
А
В
А
В
В
Б
В

Тема “Предел функции” Тест №1

  1. Отметьте верные утверждения


  • Ситуации, когда бесконечно большие величины делят друг друга или вычитают друг из друга – это ситуация неопределённости

  • произведение бесконечно большой величины и функции, которая при той же базе не стремится к нулю, есть ограниченная функция

  • односторонние пределы всегда меньше двустороннего Ответы на тесты

  1. Произведение бесконечно большой и малой величин представляет собой…


  • бесконечно малую величину

  • ситуацию неопределённости

  • ограниченную функцию

  • бесконечно большую величину
  1. 1   2   3   4   5   6   7   8   9   ...   14

Выберите два варианта ответов


Предел функции может…

Варианты ответов:


  • равняться бесконечности.

  • равняться числу.

  • стремиться сразу к двум числам

  1. Выберите один вариант ответа


Первый член числовой последовательности равен…

Варианты ответов:


  • 4

  • 1

  • 2

  • 3

  1. Выберите один вариант ответа


На числовой прямой дана точка . Тогда ее «-окрестностью» может являться интервал …

Варианты ответов:











lim

x2 16



6.





  1. ½

x4 2x2 7x 4

равен

  1. x  4 2x 1

C) 16/7

D) 8/9


  1. Вычислить



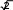A)


B) 2/3

C) -1/3

D) ∞


lim

x

  1


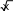x 3

  1. Дляобозначенияразличныхменяющихсявеличинприменяюттермин

а) функция б) предел в) аргумент

г) переменная

  1. Данная формула является формулой второго замечательного предела.

а) lim (1 1)x e

x x

б) lim sin x 1

x0

в) lim

xx0

x

f(x) A

г) ответ отсутствует

  1. Установить соответствие между 1 буквой и 1 цифрой

а) аргумент - это
1
не чётная

б) множество всех возможных

значений переменной х - это
2
непрерывная

в) если для всех значения

аргумента f(-х) = f(х), то эта функция
3
чётная

г) если для всех значений аргумента f(-х) = -f(х) то эта

функция
4
область определения функции

Тест №2


1. Отметьте верные утверждения

  • если односторонние пределы в некоторой точке равны, то двусторонний предел равен тому же числу

  • функция называется бесконечно малой величиной, если её предел равен нулю

  • односторонние пределы в одной и той же точке всегда равны друг другу

  • разность бесконечно большой величины и ограниченной функции есть бесконечно малая величина

1. Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является…


  • бесконечно малой величиной

  • не имеет предел

  • ситуацией неопределенности

  • бесконечно большой величиной

  1. Выберите один вариант ответа


Функция называется непрерывной в точке, если в этой точке у функции:

Варианты ответов:


  • существует предел и он не равен значению функции в этой точке.

  • существует предел и он равен значению функции в этой точке.

  • не существует предела.

  1. Выберите один вариант ответа


Точка является точкой устранимого разрыва первого рода, если в данной точке у функции:

Варианты ответов:


  • предел слева равен пределу справа, и они конечны.

  • предел слева не равен пределу справа, но оба односторонних предела конечны.

  • предел слева и предел справа равны бесконечности.

  • один из односторонних пределов равен бесконечности, а другой конечен.

Смотрите также файлы