Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 982

Скачиваний: 24

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Ответы на тесты

Выберите два варианта ответов

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №2

1. Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является…

Варианты ответов:

Варианты ответов:

Варианты ответов:

Тест №3 Отметьте верные утверждения односторонние пределы всегда меньше двустороннего сумма и разность бесконечно большой величины и ограниченной функции есть бесконечно большая величина если существует двусторонний предел, то существует и односторонние пределы равные ему же если функция монотонна и ограничена, то она не имеет предел Предел произведения функций равен… бесконечно малой величине произведению пределов этих функций бесконечно большой величине это ситуация неопределенности Впишите правильный ответ Пусть f: X R, a-предельная точка множества Х. Если функция имеет конечный предел при окрестности точки a.x a, то онав некоторой проколотой Выберите неверное утверждение: Дана функция f(x)  . x lim x0 lim x 0 lim x 0 lim f (x) не существуетf(x)  1f(x)  1f(x)  1 x  0 Отметьте примеры, в которых переход к эквивалентным совершен верно: x arcsin2 x x0x2 ; tgx sin x x0x x; C) (x 3)  sin(x 1) (x 3)(x 1) ;x0D) x2  tg(  x) x2 (  x) x Вычислить: limх3  8 12 ∞ 4 -4 x2 аrсtg(x 2) Пусть  (x) и (x)являются бесконечно малыми функциями при x a. Что можно сказать о функцияхx a (x)   (x); (x)   (x); (x) (x)при Бесконечно малая; бесконечно малая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; бесконечно малая Бесконечно малая; бесконечно большая; ничего определенного сказать нельзя Бесконечно малая; бесконечно малая; стремится к 1 Пусть f положительная бесконечно большая, а gотрицательная бесконечно большая функции при x a. Что можно сказать о функциях f g;f g;f приgx a бесконечно малая; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; Ничего определенного Ничего определенного; отрицательная бесконечно большая; бесконечно малая бесконечно малая; отрицательная бесконечно большая; бесконечно малая Установить соответствие между 1 цифрой и 1 буквой а) формула, определяющая второй замечательный предел 1 f(x1), f(x2), f(x3),… f(xn), состоящая из значенийфункции, сходится к числу А. б) формула первого замечательного предела 2 lim (1 1)x ex x в) число А называется пределом функции f(x)в точке х=х0, если для любой,сходящейся к х0последовательности x1,x2,x3,…xn…, состоящей из значений аргумента, отличных от х0,соответствующая последовательность 3 lim sin x 1x0 x г) если функция имеет областьопределения на всей числовой оси, то ее предел в точке равен 4 значению функции в этой точке Число А называется пределом функции в точке Х0, когда к Х0 сходится последовательность из значений а) аргументаб) числовой осив) координатной плоскости г) функции 1   2   3   4   5   6   7   8   9   ...   14

Ответы на тесты

Тест №1

Тест №3

Ответы на тесты

Тест №1

Тест №2

Ответы на тесты


  1. Найти неопределенный интеграл

ln 3 dx



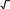
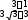ln 2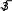

A) 8 2

B) 0 C) ln

D) ln3 ln2


  1. Найти площадь фигуры, ограниченной линиями

A) 2/3 B) 1/6π C) 1/6 D) -6

y 2x x2 ,

y x

  1. Найти площадь фигуры, ограниченной линиями y x3,

y 1 ,

x

y 8

A) 111 ln 1 B) 111 ln 1

4 8 4 8

C) 111 ln 1

D) 8

4 8

  1. Найти объем тела, полученного от вращения вокруг оси ОХ фигуры,

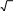ограниченной линиями yx,

y 1 ,

x

x 4

  1. -4 B)

6 3

4

  1. 4 1 4

D) 2 3

5

  1. Найти площадь фигуры, ограниченной кривыми

y 3 | x|.

A) 1,2 B) 4 C) -2 D) 0

y| x1| и

  1. Найти неопределенный интеграл ex 1 exdx.

А) 2 С

3

С) 2 С

3

В) ех 2

3

  1. arcsin

  • С

ex C

  1. Найти неопределенный интеграл

dx


x(1 ln 2 x)

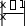
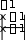A) ln2 C
C) ln x ln  C

B) ln ln x 1 C

ln x 1

D) arctg(ln x) C




  1. Найти неопределенный интеграл arccosxdx




A) 2arccosx

  1. arccosx 4

4  C

  • C

B) arccos2 x C

D) arccos2 x C




  1. Найти длину дуги кривой

Тест №3


y ln(x
x2 1),
1 x 2

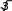A) 2 B) 1 C)

  1. Найдите первообразную для функции



  1. 3

f(x) sin x, которая в точке

x принимает значение,

2

A) Cosx+C B) –Cosx+11 C) 10Cosx D) Cosx+10

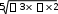  1. Найти неопределенный интеграл (x2)dx






    • 7 arcsin2x3 C

2 29



    • 7arcsin2x3 C

2 29 29

  1. ln

    • 7 arcsin2x3 C






2

7ln

29

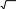
2x3 29 C

2 29

2х3 29

  1. График какой первообразной для функции

f(x)

1

1 x2

проходит

через точку с координатами (1; 2 )?

А) arctgx+(7π)/4 В) arctgх

С) arctgx+(3π)/4 D) arctgx+(9π)/4

  1. Вычислить

1/ 2 8xarctg2xdx


А) 2 2

64

1 4x2


0
В) ln 2  2

64
С) ln 2 2

64
D) 2ln2

16




  1. Вычислить

1/ 2 e2x 2exdx





А) e1 2arctg

2

e2x 1


0

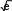
2

В) ln e1 2arctg

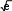2 2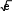

С) 1 ln e1 arctgе 3 D) 1 ln e1 2arctg

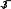2 2 2 2 2 2




  1. Вычислить

xdx


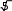А) ln В)

2ln

С) 1 ln

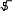
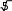2

D) 1 ln

2

  1. Не вычисляя интегралы, сравнить их:

1

1 x2 dx и

1

xdx.

 

0 0

А) > В) < С) =

  1. Не вычисляя интегралы, сравнить их.

1 x2 sin2 xdx или 1 xsin2 xdx

 

0 0

А) > В) < С) =

  1. Не вычисляя интегралы, сравнить их.

2

ln

1

xdx

или

2

ln 2 xdx.

1

А) > В) < С) =

Ответы на тесты





Тест №1

№

задания
1
2
3
4
5
6
7
8
9
10

Ответ
дифференцируема;

F(x) f(x), x X
A
B,C
C
F(b)-F(a)
C, D
A
D
B
B

Тест №2

№

задания
1
2
3
4
5
6
7
8
9
10

Ответ
B
A
C
C
A
B
B
A
B
A

Тест №3

№

задания
1
2
3
4
5
6
7
8
9
10

Ответ
C
D
A
A
C
D
C
A
B
A

Смотрите также файлы