Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 980
Скачиваний: 24
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема “Неопределенный и определенный интеграл/”
Тест №1
-
Пусть функции
f, F
определены на множестве Х. Функция F
называется первообразной функции f на множестве Х, если
на Х и.
-
Если функция f имеет первообразную на множестве Х, то она единственна?
А) Нет В) да
С) зависит от самой функции D) неопределенность
-
Выберите верные из следующих утверждений:
Пусть функции
f, g
имеют первообразные на множестве Х. Тогда
А) Совокупность всех первообразных функции fна множестве Х
исчерпывается множеством первообразных f.
{F(x) C,
C R}, где F- одна из
В)
функция
f
также имеет первообразную на Х и
f(x)dx f(x)dx
С) функция
f
также имеет первообразную на Х и
( f(x) (x))dx f(x)dx
(x))dx
D) функция
f
также имеет первообразную на Х и
( f(x) (x))dx f(x)dx
(x))dx
-
Выберите правильный ответ.
Формула интегрирования по частям в неопределенном интеграле имеет вид:
A) ( f(x) (x))dx f(x)dx (x))dx
-
f(x)dx f(x)dx -
udv uv vdu -
udv uv vdu
-
Пусть F-одна из первообразных fна отрезке [a;b]. Тогда справедлива формула Ньютона-Лейбница для вычисления определенного интеграла от
в
функции fна [a;b]: f(х)dx.
а
-
Выберите первообразные для функции
f(x)
1
.
cos2 x
А)
1
sin2 x
В) (cos x)1
С) tgx 5 D) 3 (tgx)
-
 Найти неопределенный интеграл ex 1 exdx.
Найти неопределенный интеграл ex 1 exdx.
-
 2 С
2 С
3
-
ех 2 С
 3
3-
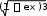 2 3
2 3 -
ех
-
ех С
-

 Выберите правильный ответ (x 3)e3xdx
Выберите правильный ответ (x 3)e3xdx
A) e3x 3e3x(x 3)
C) (x 3)e3x e3x C
B) (x2 3x)e3x
D) 1 (x 3)e3x 1 e3x C
3 9
-
Выберите правильный ответ ln 2 xdx
-
2ln
x
x C
-
xln2 x 2xln x 2x C
x
C) 1 2 C
D) 2/ x C
-
Найти неопределенный интеграл
dx
x2 4x 6
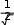 A) ln
A) ln-
arcsin
-
C
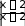
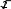 x 2 C
x 2 CB)
-
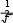
arctg C
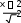 1
1x 2
Тест №2
-
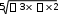 Найти неопределенный интеграл (x2)dx
Найти неопределенный интеграл (x2)dx
-
ln
-
7 arcsin2x3 C



 29 29
29 29-
-
7 arcsin2x3 C
C)

 х2 2 ln
х2 2 ln 3
2 29
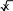 x1 C
x1 C х2
х2 D) 2х 2 С
2
-
Найти неопределенный интеграл cos7 xsin 2 xdx
A) 1 sin3 x 3 sin5 x 3 sin7 x 1 sin9 x C
3 5 7 9
B)
sin 3 x sin 7 x C
3 7
C)
cos8 x sin 3 x C
8 3
D) sin7 x cos2 x C