Файл: Сборник тестов по математике саратов2016 Содержание Тесты входного контроля по дисциплине.docx

предел слева равен пределу справа, и они конечны.
предел слева не равен пределу справа, но оба односторонних предела существуют и конечны.
предел слева и предел справа равны бесконечности.
один из односторонних пределов не существует, а другой конечен.

Вычислить

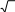lim n(

n

 n 3)

B) 5/2

C) ∞

D) -1/2

Вычислить

lim

(3  4n)²

3 3

A) -1/2

C) -8/9

D) 1/6

ⁿ^(n 3)

 (n 3)

ПеременнаяХ-это

а) функция б) предел в) аргумент

г) переменная

ЕслиданазависимостьмеждупеременнымиикаждомуХоднозначноопределено значениеУ тоэто

а) функция б) предел в) аргумент

г) переменная

Областьопределенияфункции–этомножествовсех

а) возможных значений У б) отрицательных чисел в) возможных значений Х г) положительных чисел

Тест №3

Отметьте верные утверждения

односторонние пределы всегда меньше двустороннего
сумма и разность бесконечно большой величины и ограниченной функции есть бесконечно большая величина
если существует двусторонний предел, то существует и односторонние пределы равные ему же
если функция монотонна и ограничена, то она не имеет предел

Предел произведения функций равен…

бесконечно малой величине
произведению пределов этих функций
бесконечно большой величине
это ситуация неопределенности

Впишите правильный ответ

Пусть f: X R, a-предельная точка множества Х. Если функция имеет

конечный предел при окрестности точки a.

x a, то онав некоторой проколотой

Выберите неверное утверждение: Дана функция

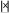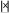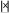f(x)  .

^lim

x0

^lim

x 0

^lim

x 0

^lim

^f⁽^x⁾не существует

f(x)  1

f(x)  1

f(x)  1

x  0

Отметьте примеры, в которых переход к эквивалентным совершен верно:

x arcsin²x

x0

x²;

tgx sin x

x0

x x;

C) (x 3)  sin(x 1) (x 3)(x 1) ;

x0

D) x² tg(  x) x²(  x)

x

Вычислить:

lim

х³ 8

12
∞
4
-4

_x_₂аrсtg(x 2)

Пусть

 (x) и

 (x)

являются бесконечно малыми функциями при

x a. Что можно сказать о функциях

x a

 (x)   (x);

 (x)   (x);

 (x)

 (x)

при

Бесконечно малая; бесконечно малая; ничего определенного сказать нельзя
Бесконечно малая; бесконечно малая; бесконечно малая
Бесконечно малая; бесконечно большая; ничего определенного сказать нельзя
Бесконечно малая; бесконечно малая; стремится к 1

Пусть ^fположительная бесконечно большая, а gотрицательная

бесконечно большая функции при x a. Что можно сказать о функциях

f g;

f g;

^fпри

g

x a

бесконечно малая; отрицательная бесконечно большая; Ничего определенного
Ничего определенного; отрицательная бесконечно большая; Ничего определенного
Ничего определенного; отрицательная бесконечно большая; бесконечно малая
бесконечно малая; отрицательная бесконечно большая; бесконечно малая

Установить соответствие между 1 цифрой и 1 буквой

а) формула, определяющая второй замечательный предел	1	f(x₁), f(x₂), f(x₃),… f(x_n), состоящая из значений функции, сходится к числу А.
б) формула первого замечательного предела	2	lim (1 ¹)^x e x _x
в) число А называется пределом функции f(x)в точке х=х₀, если для любой,сходящейся к х₀последовательности x₁,x₂,x₃,…x_n…, состоящей из значений аргумента, отличных от х₀, соответствующая последовательность	3	lim ^sin^x 1 x0 _x
г) если функция имеет область определения на всей числовой оси, то ее предел в точке равен	4	значению функции в этой точке

Число А называется пределом функции в точке Х₀, когда к Х₀ сходится последовательность из значений

а) аргумента

б) числовой оси

в) координатной плоскости г) функции

1 2 3 4 5 6 7 8 9 ... 14

Ответы на тесты

Тест №1
№ задания	1	2	3	4	5	6	7	8	9	10
Ответ	1	2	1,2	2	4	D	A	Г	А	А-2 Б-4 В-3 Г-1
Тест №2
№ задания	1	2	3	4	5	6	7	8	9	10
Ответ	1,2	1	2	1	2	B	C	В	А	В
Тест № 3
№ задания	1	2	3	4	5	6	7	8	9	10
Ответ	2,3	2	Ограниче	С	D	A	A	B	А-2	А
			на						Б-3 В-1
									Г-4

Тема “Нахождение производных функций.”

Тест №1

Производная функции y sin ³ 5xравна:

y^ 5cos³ 5x
y^ 3sin ² 5x
y^ 15sin ² 5xcos5x
y^ 15sin ² 5x

Пусть

f: X R,

-предельная точка множества Х,

a X^.

Производной функции f в точке aназывается

f(x)

f(x)  f(a)

xa

xa

x a

x0

f(a x) 

x

f(a)

lim ( f(x) 

xa

f(a))

Пусть

f: X R,

a-предельная точка множества Х,

a X. Функция ^f

называется дифференцируемой в точке a, если

A ) к. lim

xa

f(x) 

f(a)

к.

lim

x0

f(a x) 

x

f(a)

к.

lim

x0

f(a)

x

fнепрерывна в точке a

Пусть

f: X R,

a-предельная точка множества Х,

a X, ^f

дифференцируема в точке a. Дифференциалом функции f в точке a

называетсяи df(a)=

Выберите верное утверждение:

А) если fнепрерывна в точке a, то она дифференцируема в точке a

В) если fдифференцируема в точке a, то она непрерывна в точке a

С) если fнепрерывна в точке a, то она имеет конечную производную в точке

a

D) если fдифференцируема в точке a, то она имеет конечную производную

в точке a