Файл: Особенности формирования математической грамотности на уроках математики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 314
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для проведения опросов и тестов среди обучающихся использовалась программа GoogleForms, которая позволяет автоматически создавать отчёты общей статистики и по отдельным обучающимся. На диагностическом этапе исследовательской работы применялся гугл-тест.
Детям было предложено пройти гугл-тест «Математическая грамотность», ответив на 10 вопросов (для каждого класса - свой гугл-тест). Целью тестирования было выявление уровня сформированности математической грамотности обучающихся.
Содержание гугл-теста представлено в Приложении № 1. Ссылка на тест: https://docs.google.com/spreadsheets/d/1HXqEFsNt4cKtArlj1_rnJbQZFEP3B_f89ufQdnm6I/edit?usp=sharing
Итоги теста свидетельствовали о низком уровне сформированности математической грамотности обучающихся 8 класса. Результаты тестирования отражены в таблице 1 Приложения № 2, а диаграмма на рисунке 2.
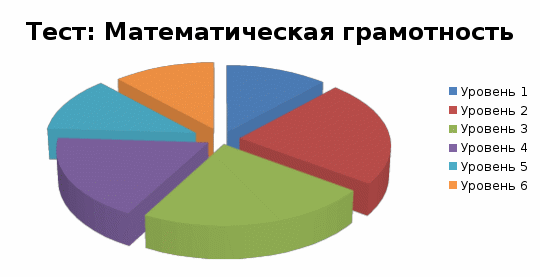
Рисунок 2. Результат тестирования «Математическая грамотность»
Формирующий этап: В рамках проведения Недели математики в школе, ребята приняли активное участие во всех проводимых мероприятиях.
Основными целями предметной недели являются:
-
Создание условий для интеллектуального, творческого развития и дальнейшего совершенствования способностей каждого учащегося. -
Развитие функциональной математической грамотности учащихся. -
Организация плодотворного сотрудничества и взаимного уважения. -
Поддержка активного стремления учащихся к получению новых и более глубоких знаний.
План мероприятий в рамках Недели математики:
| День недели | Название мероприятия | Класс |
| Понедельник | 1) Линейка, посвящённая недели математики (объявляется программа недели, оглашается состав жюри и т.п.) 2) Викторина «Знаешь ли ты историю математики?» | 5-11 кл |
| Вторник | 1) Игра «Математический поезд» 2) Викторина «Кто самый умный?» | 5-7 кл 8-11 кл |
| Среда | 1) Конкурсная игра «Зебра» 2) Конкурс творческих проектов «Талант и я!» (выставка рисунков и аппликаций с математическим содержанием, демонстрация моделей геометрических тел, ребусы и кроссворды на математические темы) 3) Защита проектов | 5-7 кл 8-11 кл |
| Четверг | 1) Конкурс – игра «Математическая литература» (составление математических стихов и сказок) 2) Игра «Математическая мозаика» | 5-7 кл 8-11 кл |
| Пятница | 1)Игры на переменах «Учусь играя» 2)Игра – конкурс «Если силён, реши!» | 5-11 кл 8-11 кл |
| Суббота | Подведение итогов Недели математики, Объявление и поздравление победителей. | 5-11 кл |
Структура сформированности уровня математической грамотности, распределялась таким образом, что для каждого компонента мы подобрали диагностический инструментарий, обеспечивающий технологическую часть диагностической программы, позволяющий оценить происходящие изменения в состоянии каждого критерия уровня математической грамотности учащихся. Центральным компонентом математической грамотности является связь.
Для того чтобы решить проблему учащийся должен сначала определить математическую природу задачи, представленную в контексте реального мира, и сформулировать их в математических терминах, затем применить математические факты, понятия, рассуждения, в последствии всё это интерпретировать и оценить. При разработке заданий учитывались принципы отбора содержания задания, мотивации школьников и разнообразие решений задач.
Так как наша работа направлена на исследование уровня математической грамотности именно учащихся 8 класса, остальные классы брать во внимание не будем.
Викторина «Знаешь ли ты историю математики?»
Цель викторины: усилить у учащихся интерес к изучению математики, расширить их кругозор, повысить уровень математической грамотности, воспитать стремление к победе в достижении новых результатов.
Правила проведения викторины:в игре участвуют учащиеся 8-11 классов. Каждый должен дать как можно больше правильных ответов на задаваемые вопросы. За каждый правильный ответ начисляется один балл. Конкурс проводится заочно. Учащиеся отвечают на вопросы викторины. Чем больше правильных ответов, тем больше количество заработанных баллов.
Методическая разработка викторины представлена в Приложении № 3.
По итогам викторины среди учащихся 8 класса историю математики знает небольшая часть класса.
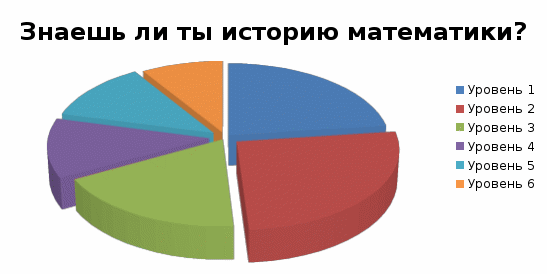
Рисунок 3. Результат викторины «Знаешь ли ты историю математики?»
Результаты ответов представлены в таблице 2 Приложения № 4.
Игра-викторина «Кто самый умный?»
Цели викторины: стимулировать интерес к предмету «Математика»; развитие логического мышления, поощрение способностей быстро соображать и принимать быстрые решения, развитие интеллекта, внимания, интуиции и находчивости обучающихся.
Правила проведения игры: в игре участвуют обучающиеся 8-11 классов. Каждый должен дать как можно больше правильных ответов на задаваемые вопросы. За каждый правильный ответ начисляется один балл. Конкурс проводится заочно. Учащиеся вместо многоточия записывают правильный ответ.
Методическая разработка игры-викторины представлена в Приложении № 5.
Викторина показала, что с предложенными вопросами справилось не более 50% класса, что вызвало у учителей большую озабоченность по планированию не только урочной, но и внеурочной деятельности.
Результаты опроса представлены в таблице 3 Приложения № 6.
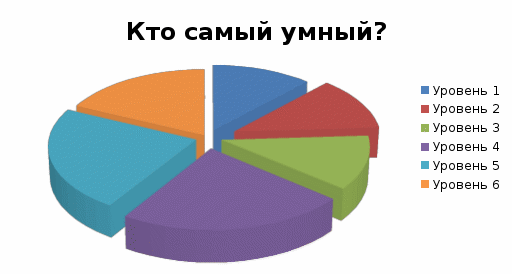
Рисунок 4. Результат тестирования «Кто самый умный?!»
Конкурс творческих проектов «Талант это я!»
ПОЛОЖЕНИЕ
о математическом конкурсе «Талант это я!»
1. Цели и задачи
1.1. Повышение интереса учащихся к математике;
1.2.Развитие творческих способностей учащихся;
1.3. Вовлечение учащихся в соревновательный процесс с целью повышения уровня их математических знаний.
2. Общие положения
2.1. Участие в Конкурсе могут принять учащиеся 8-11 классов.
2.2. Каждый участник может представить свои материалы на Конкурс в любом формате, с обязательным указанием в правом нижнем углу название работы, фамилия и имя участника, класс.
2.3. Каждый участник может представить несколько работ в нескольких номинациях.
Номинации конкурса:
1. Конкурс рисунков из геометрических фигур и цифр.
2. Конкурс ребусов (на конкурс принимаются материалы в сопровождении правильных ответов).
3. Конкурс кроссвордов (на конкурс принимаются материалы в сопровождении правильных ответов).
4. Конкурс поделок (геометрические фигуры).
3. Награждение
3.1. Результаты конкурса будут суммироваться с учетом возрастной категории каждого номинанта, и экспонироваться на «Выставке творческих математических работ».
Работа, подготовленная несколькими учащимися, оценивается единым дипломом на всех авторов.
3.2.Учащимся, не вошедшим в число призёров, будут вручены сертификаты участников.
Наградные документы вручаются на линейке по подведению итогов Недели математики.
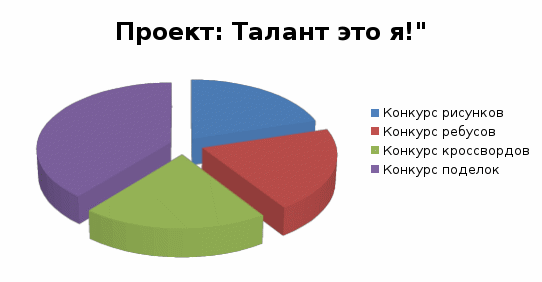
Рисунок 5. Результат проекта «Талант и я!»
Результаты проекта представлены в таблице 4 [см. Приложение№ 7].
Игра «Математическая мозаика»
Цели игры: развивать и укреплять интерес учащихся к предмету «Математика», расширить их кругозор, повышение уровня их математической грамотности; демонстрация красоты науки «Математика» в окружающем мире и её тесной взаимосвязи с различными областями применения; развитие коммуникативных навыков, уверенности в себе и раскованности в общении.
Вопросы игры разбиты на шесть категорий:
-
«Великие и знаменитые» -
«Шифровальщик»
-
«Карта мира» -
«Мир культуры» -
«Чудеса природы» -
«Среднее арифметическое»
Каждая команда выбирает на экране категорию вопроса и её стоимость. Право выбора первого вопроса проводиться путём жеребьёвки. Команда, которая первой поднимет сигнальную карточку, имеет право первой отвечать на вопрос. Если команда правильно ответила на вопрос, на её счёт зачисляются «очки» и команда имеет право выбирать следующий вопрос. В случае если команда даёт неверный ответ, право хода переходит к команде соперников.Побеждает команда, набравшая большее количество «очков».
Методическая разработка представлена в [см. Приложение № 8].
Рисунок 6 Результат викторины «Математическая мозаика»
Результаты игры представлены в таблице 5[см. Приложение № 9].
Конкурс - игра «Если силён, реши!»
Цель: формирование устойчивого интереса школьников к изучению предмета «Математика».
Задачи:
1) Уметь применять полученные на уроках знания к нестандартным ситуациям.
2) Активировать творческие способности школьников, развивать воображение, логическое мышление, находчивость, смекалку.
3) Развивать чувство взаимной поддержки, уверенности в себе, умение быстро сосредоточиться на главном в процессе коллективной работы.
4) Развивать чувства собственного достоинства, самоконтроля и взаимоконтроля.
Оборудование: карточки с заданиями.
Правила проведения конкурса:
- Задания изображены на отдельных карточках, каждое задание оценивается в 1 балл. Учащиеся выбирают карточки с задачами, содержащие ребусы, кроссворды, задания и т.п.
- На этой же карточке учащиеся пишут своё имя, фамилию и ответ.
- Карточку с ответами помещают в специальный ящик, который находится в кабинете математики.
Подведение итогов: Задания выполняются в течении учебного дня. В конце дня составляется протокол, отражающий результаты конкурса. Определение победителей.
Методическая разработка представлена в [см. Приложение№ 10]
Рисунок 6. Результат игры «Если силён, реши!»
Результаты конкурса - игры представлены в таблице 6 [см. Приложение № 11]
Подведение итогов Недели математики.
Награждение победителей.
Аналитический этап-это этап работы, который был посвящён теоретическому обобщению результатов исследования, процесса развития уровня математической грамотности обучающихся 8 класса в условиях реализации внеклассной работы с применением методов статистической обработки.
Рассмотрим результаты диагностики. Результаты диагностического среза показали, что у восьмиклассников сформирован средний уровень математической грамотности. Сильнее выражена потребность в использовании математических знаний и умений на практике.
С помощью гугл-теста мы провели повторное итоговое тестирование, позволяющее выявить уровень математической грамотности учащихся 8 класса, заменив вопросы на более сложные.