Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc

В полупроводниках обычно наблюдается недостаток электронов проводимости; они высвобождаются только при подводе тепловой энергии (повышении температуры). В этом случае с повышением температуры увеличивается количество свободных электронов и электрическое сопротивление уменьшается. Увеличение их электрической проводимости с повышением температуры приблизительно выражается экспоненциальной функцией

R₂ = R₁exp b(1/T₂ – 1/T₁), (3)
где R₂ и R₁ – значения сопротивления (Ом) чувствительного элемента при абсолютной температуре Т₂ [K] и при эталонной температуре Т₁, например при Т₁ = 273,15 К; b – некоторая постоянная величина, зависящая от материала; ее численное значение может составлять 3000 – 4000 К.

Экспоненциальная характеристика, описываемая этой формулой, имеет большой и сильно изменяющийся температурный коэффициент , благодаря которому терморезисторы получили распространение в лабораторной и производственной практике. У терморезисторов NTC он изменяется в диапазоне от –1 до – 6 К^-1. Сопротивления самих терморезисторов колеблется от 1 кОм до 1 МОм; в сравнении с ним изменения сопротивления на клемах и в соединительных проводах незначительны и ими можно пренебречь. Это является одним из существенных преимуществ терморезисторов перед обычными термометрами сопротивления и термопарами.

Терморезисторы NTC изготавливают из смесей оксидов металлов, которые спекаются при высоких температурах, образуя маленькие шарики, пластинки или стерженьки размерами менее 1 мм. Однако в зависимости от места установки каждый чувствительный элемент должен быть защищен – обычно тонкой стеклянной, керамической или стальной оболочкой.

Для измерения сопротивления используют преимущественно электрические схемы в виде мостов. Линеаризация нелинейной зависимости между температурой Т и сопротивлением R для всех чувствительных элементов термометров сопротивления обеспечивается операционными усилителями либо при помощи микропропроцессоров или ПЭВМ.
3. Термоэлектрические термометры.

Зеебек установил, что если электрическая цепь состоит из двух различных металлов или сплавов и точки их соединения (спаи) находятся при различных температурах, то в цепи должен протекать ток, рис.4. При

---

^{металл А металл А}
t ₁ t₀ t₁ t<sub>0

металл B металл B</sub>



Р ис.4. Термоэлектрический эффект Зеебека.
размыкании цепи на ее концах можно измерить разность потенциалов - так называемую термоэлектродвижущую силу (т.э.д.с.), которая будет мерой разности между измеряемой температурой Т₁ и контрольной температурой Т₀ холодного спая.

Зависимость между т.э.д.с. и разностью температур в общем случае нелинейна и может быть выражена уравнением третьей степени. Однако при небольших изменениях температур характеристики многих термопар могут быть линеаризованы без большого ущерба для точности:

Е = кТ [мВ], (4)
где к – коэффициент т.э.д.с., зависящий также и от уровня температуры, мВ/К.

Используя уравнение для т.э.д.с., можно для каждой комбинации материалов термопары построить график зависимости т.э.д.с. термопары от измеряемой температуры Т₁, полагая, что температура ее другого спая Т₀ = 0 ⁰С. Если контрольная температура Т₀  0 ⁰С, а поддерживается постоянной или даже вообще непостоянна, то в измеренное значение т.э.д.с. Е_и нужно внести поправку Е_к, которая соответствует отклонению контрольной температуры от Т₀ = 0 ⁰С:

Е = Е_и + Е_к.

В приборах для измерения температуры при помощи термопар температура спая Т

---

₀ может измеряться с помощью терморезистора, а значение т.э.д.с. автоматически исправляется по этой формуле при обработке результатов измерения микропроцессором или ПЭВМ.
Порядок выполнения задания.

1. 
   Тумблером «сеть» включить напряжение питания прибора.
   

При этом многоканальный измерительный прибор автоматически устанавливается на измерение температуры в первом канале, т.е. температуры образцового термометра.

2. 
   Тумблером «нагрев» включить нагрев воды в стакане, в который вставлены электрические термометры. При достижении определенной температуры нагрев прекратить, показания температуры образцового термометра перестанут увеличиваться.
   

3. Нажать два раза на сенсор «» измерительного прибора, чтобы включить «Циклический вывод» - смена каналов измерений начнет осуществляется автоматически по циклу.

НЕ НАЖИМАТЬ ДРУГИХ СЕНСОРОВ!!!!!

4. 
   Подождать несколько минут пока не установится тепловое равновесие пластины. Записать в таблицу результаты измерений остывания воды для всех 5 термометров.
   
5. 
   Построить графики зависимости сопротивления и т.э.д.с. от температуры образцового термометра для 4, 5, 6 и 7 термометров.
   
6. 
   По формулам (2), (3) и (4) определить постоянные величины , b и к для соответствующих термометров.
   

На основании проделанных измерений сформулировать цель работы и сделать выводы.
Контрольные вопросы

1. 
   Что такое “термометрическое тело и термометрическая величина”?
   
2. 
   Какие температурные шкалы и единицы измерения используются для определения температуры?
   
3. 
   Как объяснить зависимость сопротивления от температуры для полупроводникового и металлического термометров?
   
4. 
   Какой физический смысл линейного температурного коэффициента сопротивления? От чего он зависит?
   
5. 
   Какой физический смысл коэффициента т.э.д.с.? От чего зависит этот коэффициент?
   

ЛИТЕРАТУРА:

1. 
   Измерения в промышленности. Справочник, Т.2.,1990. М., Металлургия.
   
2. 
   Сосновский А.Г., Столярова Н.И. Измерения температур, 1970. М.
   
3. 
   Датчики физических величин. Дж. Аш и соавторы. Перевод с французского. Т. 1, 1990, М.
   

Экспериментальная установка состоит из прозрачного пластмассового стакана 2, в который налита вода и вставлены пять электрических термометров: образцовый термометр 3, металлический термометр сопротивления 4, полупроводниковый термометр сопротивления 5, термопары типа ТХА 6 и ТХК 7, измеряемые сигналы которых поступают в измерительный прибор (измеритель-регулятор «Сосна-002») 8. Нагреватель 1

---

находится на дне стакана и нагревает воду, температура которой измеряется пятью различными термометрами. Стакан с нагревателем закреплены на платформе. Измерительный прибор инициирует последовательно результаты измеренных сигналов от каждого термометра (верхнее табло) и номер термометра (нижнее табло). Цикл измерения длится 1 минуту. Единицы измерения образцового термометра – [⁰С], термометров сопротивления – [Ом], термопар - [мВ].
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. 
   Тумблером «сеть» включить напряжение питания прибора.
   

При этом многоканальный измерительный прибор автоматически устанавливается на измерение температуры в первом канале, т.е. температуры образцового термометра.

2. Тумблером «нагрев» включить нагрев воды в стакане, в котором находятся электрические термометры. При достижении температуры кипения воды нагреватель выключить.

3. 
   Нажать два раза на сенсор «» измерительного прибора, чтобы включить «Циклический вывод» - смена каналов измерений начнет осуществляется автоматически по циклу.
   

НЕ НАЖИМАТЬ ДРУГИХ СЕНСОРОВ!!!!!

4. 
   Подождать несколько минут пока не установится тепловое равновесие воды в стакане. Записать в таблицу результаты измерений остывания воды для всех 5 термометров.
   
5. 
   Построить графики зависимости сопротивления и т.э.д.с. от температуры образцового термометра для 4, 5, 6 и 7 термометров.
   
6. 
   По формулам (2), (3) и (4) определить постоянные величины , b и к для соответствующих термометров.
   

ЛИТЕРАТУРА:

2. 
   Измерения в промышленности. Справочник, Т.2.,1990. М., Металлургия.
   
3. 
   Сосновский А.Г., Столярова Н.И. Измерения температур, 1970. М.
   
4. 
   Датчики физических величин. Дж. Аш и соавторы. Перевод с французского. Т. 1, 1990, М.
   

---

Лабораторная работа№7

Измерение коэффициента теплопроводности сыпучих тел.
Цель работы: измерить коэффициент теплопроводности кварцевого песка.

Оборудование и принадлежности: источник питания, вольтметр-амперметр, цилиндр с кварцевым песком, термопара.
Элементы теории.

Процесс переноса теплоты из области тела с более высокой температурой в области, где она ниже, называется теплопроводностью.

Плотность потока теплоты

(1)

где - количество теплоты, проходящее за время через площадку S ; единичный вектор, перпендикулярный к площадке и совпадающий с направлением распространения теплоты. Величина q показывает, какое количество теплоты переносится в единицу времени через единичную площадку, перпендикулярную к направлению распространения теплоты.

Предположим, что в неограниченной среде перенос теплоты происходит в одном направлении, вдоль которого направим ось Х . Тогда вектор будет иметь только одну составляющую , зависящую от одной координаты х и времени t,
(2)
где единичный вектор оси Х.


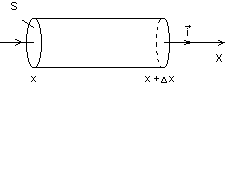
Рис.1

Мысленно выделим в среде цилиндр длинной , площадью основания S , с образующей, параллельной оси Х, (рис.1). Количество теплоты, поступающее в выделенный объем через сечение с координатой за время

---